Что из перечисленного ниже есть система различных представителей для системы подмножеств 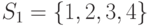 ,
, 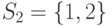 ,
,  ,
, 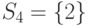 исходного множества
исходного множества 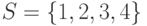
(Отметьте один правильный вариант ответа.)
Варианты ответа

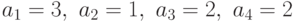
не существует системы различных представителей для данной системы подмножеств(Верный ответ)

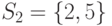 ,
, 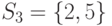 ,
, 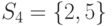 исходного множества
исходного множества 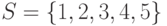
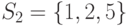 ,
,  при разбиениях множества
при разбиениях множества 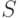
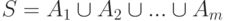 и
и 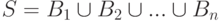 , для
, для 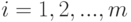 ,
, 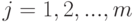 :
: множеств
множеств 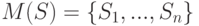 для первых
для первых  множеств,
множеств, 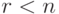 , удалось выбрать различных представителей, но все элементы множества
, удалось выбрать различных представителей, но все элементы множества 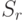 уже использованы в качестве представителей предыдущих множеств. Тогда:
уже использованы в качестве представителей предыдущих множеств. Тогда: , состоящего из
, состоящего из  ,
,  , элементов стоят на своих местах, а остальные
, элементов стоят на своих местах, а остальные 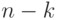 элементов расположены случайно:
элементов расположены случайно: различным ящикам, при условии, что в каждом ящике находится
различным ящикам, при условии, что в каждом ящике находится 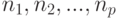 объектов соответственно,
объектов соответственно, 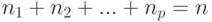 , и один из размещаемых объектов уже лежит в ящике
, и один из размещаемых объектов уже лежит в ящике  :
: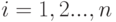 последовательно выбрали
последовательно выбрали 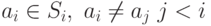 . Тогда выбранный набор
. Тогда выбранный набор 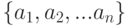 :
: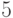 объектов на
объектов на  непустых класса равно
непустых класса равно 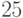 . Вычислите количество сюръективных отображений из множества, содержащего
. Вычислите количество сюръективных отображений из множества, содержащего  объектов на
объектов на 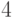 непустых класса равно
непустых класса равно  . Вычислите количество сюръективных отображений из множества, содержащего
. Вычислите количество сюръективных отображений из множества, содержащего