Что означает запись 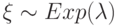 ?
?
(Отметьте один правильный вариант ответа.)
Варианты ответа
![\begin{equation} \begin{matrix} \ p_{\xi}(x) = \left\{ \begin{matrix} \frac 1{b-a} & x\in [a,b] \\ 0 & x\notin [a,b] } \end{matrix} \right. \end{matrix}\end{equation}](https://intuit.ru//sites/default/files/tex_cache/b17b2bc518d4f9ac0e8c4af5a58f02b3.png)
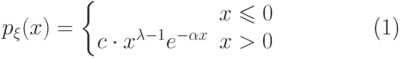

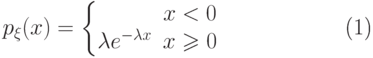 (Верный ответ)
(Верный ответ)

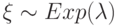 ?
?![\begin{equation} \begin{matrix} \ p_{\xi}(x) = \left\{ \begin{matrix} \frac 1{b-a} & x\in [a,b] \\ 0 & x\notin [a,b] } \end{matrix} \right. \end{matrix}\end{equation}](https://intuit.ru//sites/default/files/tex_cache/b17b2bc518d4f9ac0e8c4af5a58f02b3.png)
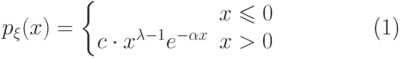

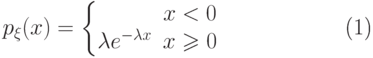 (Верный ответ)
(Верный ответ)
 вероятность ровно
вероятность ровно  успехов в
успехов в  испытаниях по схеме Бернулли, если вероятность успеха в одном испытании
испытаниях по схеме Бернулли, если вероятность успеха в одном испытании  зависит от количества испытаний
зависит от количества испытаний  , зависимость
, зависимость 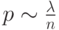 , где постоянная
, где постоянная  ?
? . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Допустим,
. Допустим, 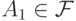 . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в 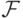 кроме
кроме  ?
? . Какое условие на
. Какое условие на 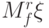 -
-  -ые факториальные моменты должно выполняться, чтобы
-ые факториальные моменты должно выполняться, чтобы 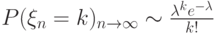 ?
? . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что является наиболее точной верхней оценкой мощности
. Что является наиболее точной верхней оценкой мощности 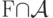 ?
? . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что верно относительно мощности
. Что верно относительно мощности 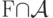 ?
? . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что верно относительно
. Что верно относительно 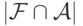 ?
? . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  .Среди множеств
.Среди множеств 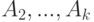 и
и  выберите множество, с котором не пересекается
выберите множество, с котором не пересекается 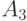 .
. . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  .Среди множеств
.Среди множеств 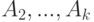 и
и  выберите множество, с котором не пересекается
выберите множество, с котором не пересекается 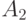 .
.