В формуле оценки количества различных (как графы с занумерованными вершинами) унициклических графов с  вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах
вершинах 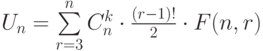 выражение
выражение 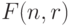 показывает...
показывает...
(Отметьте один правильный вариант ответа.)
Варианты ответа
число способов зафиксировать цикл
число способов зафиксировать вершины для цикла
число способов построить цикл на выбранных вершинах
число различных (как графы с занумерованными вершинами) лесов с  деревьями с общим количеством вершин
деревьями с общим количеством вершин  , такое, что первое дерево содержит вершину 1, второе – вершину 2, …,
, такое, что первое дерево содержит вершину 1, второе – вершину 2, …,  -ое дерево содержит вершину
-ое дерево содержит вершину  (Верный ответ)
(Верный ответ)
 деревьями с общим количеством вершин
деревьями с общим количеством вершин  , такое, что первое дерево содержит вершину 1, второе – вершину 2, …,
, такое, что первое дерево содержит вершину 1, второе – вершину 2, …,  -ое дерево содержит вершину
-ое дерево содержит вершину  (Верный ответ)
(Верный ответ)

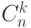 показывает...
показывает...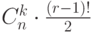 показывает...
показывает...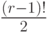 показывает...
показывает...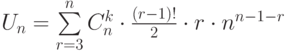 выражение
выражение 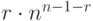 показывает...
показывает...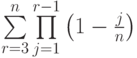 заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых ![S_1+S_2=\sum\limits_{r=3}^{\left[n^{0,6}\right]}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)+\sum\limits^{n}_{r= \left [n^{0,6} \right]+1}}\prod\limits_{j=1}^{r-1} \left (1-\frac{j} {n} \right)](https://intuit.ru//sites/default/files/tex_cache/fa9abca000854ee9146e5639e6678f0b.png) .При указанном интервале суммирования для
.При указанном интервале суммирования для 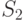 , что является нижней оценкой величины
, что является нижней оценкой величины 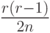 ?
?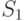 ?
? ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Допустим,
. Допустим, 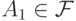 . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в 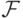 кроме
кроме  ?
?