Какой знак можно поставить между числом упорядоченных разбиений числа  на
на  слагаемых и числом упорядоченных разбиений числа
слагаемых и числом упорядоченных разбиений числа  ?
?
(Отметьте один правильный вариант ответа.)
Варианты ответа
 (Верный ответ)
(Верный ответ)



 на
на  - количество различных неупорядоченных разбиений числа
- количество различных неупорядоченных разбиений числа 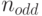 - количество различных неупорядоченных разбиений числа
- количество различных неупорядоченных разбиений числа 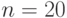 ?
?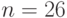 ?
?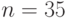 ?
?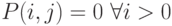 в рекуррентной формуле количества разбиений числа
в рекуррентной формуле количества разбиений числа  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Допустим,
. Допустим, 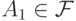 . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в 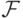 кроме
кроме  ?
?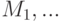
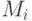 , тогда существует одноцветная раскраска данного
, тогда существует одноцветная раскраска данного