Пусть случайная величина  , математическое ожидание квадрата данной случайной величины конечно
, математическое ожидание квадрата данной случайной величины конечно  и имеется
и имеется 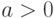 . Какое утверждение, согласно неравенству Чебышева, является верным?
. Какое утверждение, согласно неравенству Чебышева, является верным?
(Отметьте один правильный вариант ответа.)
Варианты ответа
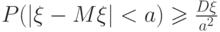

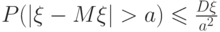 (Верный ответ)
(Верный ответ)
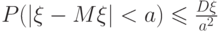

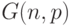 -случайный граф, множество, состоящее из
-случайный граф, множество, состоящее из  вершин, а каждое ребро проводим с вероятностью
вершин, а каждое ребро проводим с вероятностью  , которая независит от вероятности проведения других ребер и может зависеть от
, которая независит от вероятности проведения других ребер и может зависеть от 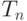 - число треугольников в случайном графе. Если
- число треугольников в случайном графе. Если 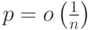 , то к чему ассимтотические стремится математическое ожидание
, то к чему ассимтотические стремится математическое ожидание  ?
? , то чему ассимптотически равна величина
, то чему ассимптотически равна величина  ?
?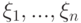 , определенные на некотором
, определенные на некотором  , если для любого
, если для любого 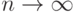 выполняется условие
выполняется условие 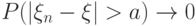 , то говорят, что
, то говорят, что 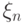 сходится к
сходится к 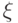 ...
... принимает только 4 значения:
принимает только 4 значения:  .Известно, что
.Известно, что 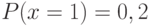 ,
, 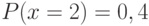 ,
, 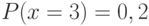 . Чему равно математическое ожидание
. Чему равно математическое ожидание 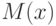 ?
?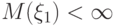 . С каким типом сходимости
. С каким типом сходимости 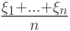 сходится к
сходится к  при
при  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Допустим,
. Допустим, 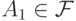 . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в 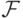 кроме
кроме  ?
?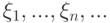 , у которых математическое ожидание конечно
, у которых математическое ожидание конечно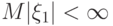 . C каким самым сильным типом сходимости при
. C каким самым сильным типом сходимости при 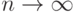 последоваетельность случайных величин
последоваетельность случайных величин 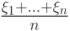 сходится к
сходится к 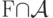 ?
? бесконечная последовательность независимых событий:
бесконечная последовательность независимых событий: 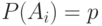 . Положим
. Положим 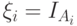 . Тогда с каким самым сильным из предложенных типом сходимости при
. Тогда с каким самым сильным из предложенных типом сходимости при 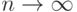 случайная величина
случайная величина  сходится к 0?
сходится к 0? ,у которого
,у которого 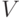 – множество вершин и
– множество вершин и  – множество ребер.
– множество ребер. число независимости и
число независимости и  кликовое число. Какое утверждение является верным?
кликовое число. Какое утверждение является верным?