Пусть 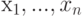 - выборка. Предполжим, что выборка является реализацией некоторых одинаково распределенных, независимых случайных величин
- выборка. Предполжим, что выборка является реализацией некоторых одинаково распределенных, независимых случайных величин 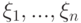 . Пусть
. Пусть 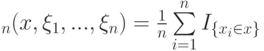 - эмпирическая функция распределения. Какое утверждение относительно ее является верным?
- эмпирическая функция распределения. Какое утверждение относительно ее является верным?
(Отметьте один правильный вариант ответа.)
Варианты ответа
![P\left(\sup\limits_{x\in R}\left|\hat{F}_n(x,\xi_1,...,\xi_n)-F_{\xi_1}(x)\right|\xrightarrow[n\to\infty]{}0\right)=1](https://intuit.ru//sites/default/files/tex_cache/8d04ecd116a0d066d97dbca0a7f4d090.png) (Верный ответ)
(Верный ответ)
![P\left(\sup\limits_{x\in R}\left|\hat{F}_n(x,\xi_1,...,\xi_n)-F_{\xi_1}(x)\right|\xrightarrow[n\to\infty]{}1\right)=0](https://intuit.ru//sites/default/files/tex_cache/c40d4775e059f9a2655d540a9dcd38ee.png)
![P\left(\sup\limits_{x\in R}\left|\hat{F}_n(x,\xi_1,...,\xi_n)-F_{\xi_1}(x)\right|\xrightarrow[n\to\infty]{}1\right)=1](https://intuit.ru//sites/default/files/tex_cache/0e375e4905a33824d8e930248ee838db.png)
![P\left(\sup\limits_{x\in R}\left|\hat{F}_n(x,\xi_1,...,\xi_n)-F_{\xi_1}(x)\right|\xrightarrow[n\to\infty]{}0\right)=0](https://intuit.ru//sites/default/files/tex_cache/4474e47a197bad8c2a9e72d3fcc45d57.png)

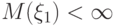 . С каким типом сходимости
. С каким типом сходимости 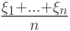 сходится к
сходится к  при
при 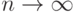 ?
?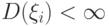 и сходится ряд
и сходится ряд 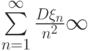 . С каким типом сходимости
. С каким типом сходимости 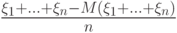 сходится к
сходится к  при
при 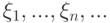 , у которых математическое ожидание конечно
, у которых математическое ожидание конечно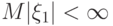 . C каким самым сильным типом сходимости при
. C каким самым сильным типом сходимости при 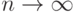 последоваетельность случайных величин
последоваетельность случайных величин 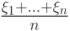 сходится к
сходится к 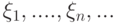 . Обозначим
. Обозначим 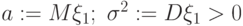 . Тогда с каким типом сходимости при
. Тогда с каким типом сходимости при  сходится к
сходится к 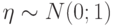 ?
?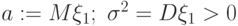 . Чему равна характеристическая функция для
. Чему равна характеристическая функция для  ?
? . Тогда
. Тогда  при
при  ?
?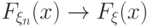 в любой
в любой  - точки непрерывности
- точки непрерывности 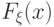 , то говорят, что
, то говорят, что 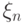 сходится к
сходится к 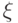 ...
... , если для любого
, если для любого 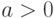 при
при 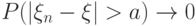 , то говорят, что
, то говорят, что 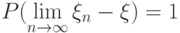 , то говорят, что
, то говорят, что