Пусть  и
и 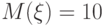 . Какое число будет стоять в правой части неравенства Маркова для этого случая
. Какое число будет стоять в правой части неравенства Маркова для этого случая 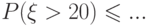
(Ответ необходимо ввести в поле ввода.)
Варианты ответа

 и
и 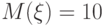 . Какое число будет стоять в правой части неравенства Маркова для этого случая
. Какое число будет стоять в правой части неравенства Маркова для этого случая 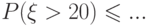
 . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Допустим,
. Допустим, 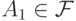 . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в 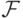 кроме
кроме  ?
?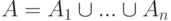 . Введем на подмножествах множества индексов
. Введем на подмножествах множества индексов  функцию
функцию 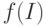 , где
, где 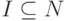 . Пусть
. Пусть 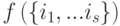 обозначает число элементов множества
обозначает число элементов множества  , которые могут не принадлежать каким-то из подмножеств
, которые могут не принадлежать каким-то из подмножеств 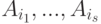 , но обязаны принадлежать каждому из остальных подмножеств. Чему равно
, но обязаны принадлежать каждому из остальных подмножеств. Чему равно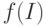 при
при 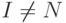 ?
? ,у которого
,у которого 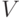 – множество вершин и
– множество вершин и  – множество ребер.
– множество ребер. число независимости и
число независимости и  кликовое число. Какое утверждение является верным?
кликовое число. Какое утверждение является верным? . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что является наиболее точной верхней оценкой мощности
. Что является наиболее точной верхней оценкой мощности 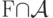 ?
? ,у которого
,у которого 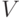 – множество вершин и
– множество вершин и  – множество ребер.
– множество ребер.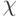 хроматическое число и
хроматическое число и  - кликовое число. Какое утверждение является верным?
- кликовое число. Какое утверждение является верным? . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что верно относительно мощности
. Что верно относительно мощности 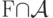 ?
? . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что верно относительно
. Что верно относительно 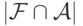 ?
?