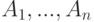 - события. Пусть
- события. Пусть 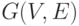 произвольный орграф зависимостей. И существуют
произвольный орграф зависимостей. И существуют  , что выполняется
, что выполняется 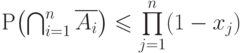 . Что верно относительно
. Что верно относительно  ?
?
(Отметьте один правильный вариант ответа.)
Варианты ответа
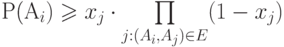
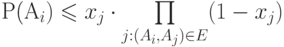 (Верный ответ)
(Верный ответ)



 выполнено
выполнено  . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что верно относительно мощности
. Что верно относительно мощности 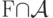 ?
?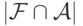 ?
?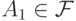 . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в 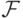 кроме
кроме  ?
? на
на  -вероятность покрасить ребро в красный цвет и
-вероятность покрасить ребро в красный цвет и  - вероятность покрасить ребро в синий цвет. Определим события
- вероятность покрасить ребро в синий цвет. Определим события 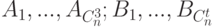 , где
, где  -состоит в том, что
-состоит в том, что 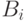 -состоит в том, что
-состоит в том, что  целиком синяя. Если для некоторого события
целиком синяя. Если для некоторого события 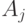 ?
?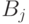 ?
? . Из множества
. Из множества  выбираем случайные подмножества
выбираем случайные подмножества  и
и  из
из  , где
, где ![m=\left[\frac{8d}{\epsilon} log_2 \frac{8d}{\epsilon} \right]](https://intuit.ru//sites/default/files/tex_cache/6049bf901b7724dca7ef621a2a8f67b5.png) по схеме выбора с возращением
по схеме выбора с возращением 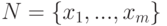 . Пусть определены события
. Пусть определены события 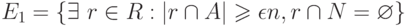 и
и  . Если известно
. Если известно 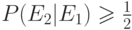 , что является верным относительно
, что является верным относительно 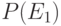 и
и  ?
?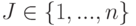 при выполнении некоторого ограничения на множество
при выполнении некоторого ограничения на множество 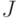 выполняется равенство
выполняется равенство  . Какое условие накладывается на множество
. Какое условие накладывается на множество