Пусть 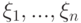 , каждая из которых принимает значение 1 с вероятностью
, каждая из которых принимает значение 1 с вероятностью  и значение 0 с вероятностью
и значение 0 с вероятностью  . Согласно усиленному закону больших чисел для схемы Бернулли c каким самым сильным типом сходимости случайная величина
. Согласно усиленному закону больших чисел для схемы Бернулли c каким самым сильным типом сходимости случайная величина 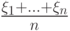 сходится при
сходится при 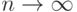 к
к  ?
?
(Отметьте один правильный вариант ответа.)
Варианты ответа
почти наверное(Верный ответ)
по вероятности
по распределению
в среднем

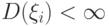 и сходится ряд
и сходится ряд 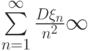 . С каким типом сходимости
. С каким типом сходимости 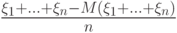 сходится к
сходится к  при
при 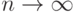 ?
?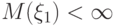 . С каким типом сходимости
. С каким типом сходимости 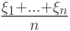 сходится к
сходится к  при
при 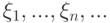 , у которых математическое ожидание конечно
, у которых математическое ожидание конечно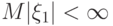 . C каким самым сильным типом сходимости при
. C каким самым сильным типом сходимости при 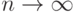 последоваетельность случайных величин
последоваетельность случайных величин 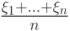 сходится к
сходится к 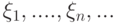 . Обозначим
. Обозначим 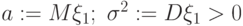 . Тогда с каким типом сходимости при
. Тогда с каким типом сходимости при  сходится к
сходится к 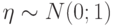 ?
? , если для любого
, если для любого 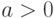 при
при 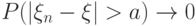 , то говорят, что
, то говорят, что 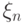 сходится к
сходится к 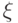 ...
...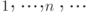 бесконечная последовательность независимых событий:
бесконечная последовательность независимых событий: 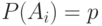 . Положим
. Положим 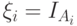 . Тогда с каким самым сильным из предложенных типом сходимости при
. Тогда с каким самым сильным из предложенных типом сходимости при  сходится к 0?
сходится к 0?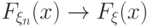 в любой
в любой  - точки непрерывности
- точки непрерывности 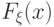 , то говорят, что
, то говорят, что 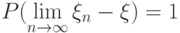 , то говорят, что
, то говорят, что 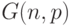 -случайный граф, множество, состоящее из
-случайный граф, множество, состоящее из  вершин, а каждое ребро проводим с вероятностью
вершин, а каждое ребро проводим с вероятностью 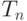 - число треугольников в случайном графе. Если
- число треугольников в случайном графе. Если  , то чему ассимптотически равна величина
, то чему ассимптотически равна величина  ?
?