Какая формула определяет количество размещений из  элементов по
элементов по  без повторений?
без повторений?
(Отметьте один правильный вариант ответа.)
Варианты ответа
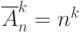
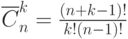

 (Верный ответ)
(Верный ответ)

 элементов по
элементов по  без повторений?
без повторений?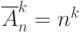
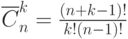

 (Верный ответ)
(Верный ответ)
 . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Допустим,
. Допустим, 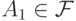 . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в 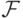 кроме
кроме  ?
? , из которого выбираются сочетания по
, из которого выбираются сочетания по  элементов. Из множества всех возможных сочетаний выбрали подмножество
элементов. Из множества всех возможных сочетаний выбрали подмножество 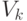 , в котором ровно
, в котором ровно  элементов принадлежат
элементов принадлежат 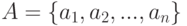 .Найдите мощность
.Найдите мощность 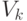 .
. вероятность ровно
вероятность ровно  успехов в
успехов в  испытаниях по схеме Бернулли, если вероятность успеха в одном испытании
испытаниях по схеме Бернулли, если вероятность успеха в одном испытании  зависит от количества испытаний
зависит от количества испытаний  , зависимость
, зависимость 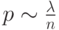 , где постоянная
, где постоянная  ?
? . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что является наиболее точной верхней оценкой мощности
. Что является наиболее точной верхней оценкой мощности 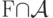 ?
? . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что верно относительно мощности
. Что верно относительно мощности 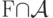 ?
? . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что верно относительно
. Что верно относительно 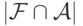 ?
?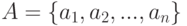 и множество
и множество 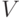 – все размещения с повторениями из элементов множества по
– все размещения с повторениями из элементов множества по  по
по  . Известно, что
. Известно, что  . Рассмотрим свойство
. Рассмотрим свойство  которым или обладает или не обладает каждый элемент из множества
которым или обладает или не обладает каждый элемент из множества 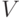 . Размещение обладает свойством
. Размещение обладает свойством  , если элемент
, если элемент 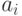 не принадлежит данному размещению. Сколько
не принадлежит данному размещению. Сколько  размещений не обладает ни одним из свойств
размещений не обладает ни одним из свойств  ?
?