Какая формула эквивалентна следующему высказыванию относительно чисел Рамсея: существует раскраска ребер полного графа  , при которой нет ни одной красной клики
, при которой нет ни одной красной клики  и ни одной синей клики
и ни одной синей клики 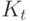 ?
?
(Отметьте один правильный вариант ответа.)
Варианты ответа
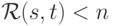

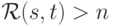 (Верный ответ)
(Верный ответ)

 состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика 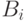 состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  целиком красная или существует клика размера
целиком красная или существует клика размера  целиком синяя?
целиком синяя? называется минимальное число
называется минимальное число  такое, что при любой раскраске полного графа
такое, что при любой раскраске полного графа  , у которого все ребра красные, либо существует подграф
, у которого все ребра красные, либо существует подграф 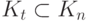 , у которого все ребра синие. Чему равен порядок
, у которого все ребра синие. Чему равен порядок 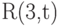 ?
?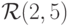 ?
?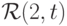 ?
? ?
? ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что верно относительно мощности
. Что верно относительно мощности 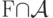 ?
?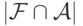 ?
?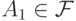 . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в 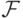 кроме
кроме  ?
?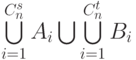 ?
?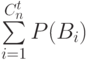 ?
?