Пусть 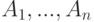 события. Формулировка "любое событие
события. Формулировка "любое событие  независит от остальных событий кроме не более чем
независит от остальных событий кроме не более чем  штук" означает, что ...
штук" означает, что ...
(Отметьте один правильный вариант ответа.)
Варианты ответа
из множества 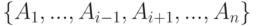 найдется подмножество
найдется подмножество 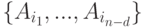 , состоящее из событий, от совокупности которых
, состоящее из событий, от совокупности которых  не зависит
не зависит
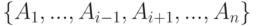 найдется подмножество
найдется подмножество 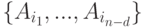 , состоящее из событий, от совокупности которых
, состоящее из событий, от совокупности которых  не зависит
не зависит
из множества 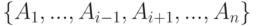 найдется подмножество
найдется подмножество 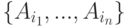 , состоящее из событий, от совокупности которых
, состоящее из событий, от совокупности которых  не зависит
не зависит
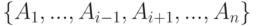 найдется подмножество
найдется подмножество 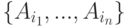 , состоящее из событий, от совокупности которых
, состоящее из событий, от совокупности которых  не зависит
не зависит
из множества 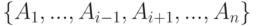 найдется подмножество
найдется подмножество 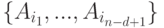 , состоящее из событий, от совокупности которых
, состоящее из событий, от совокупности которых  не зависит
не зависит
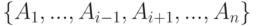 найдется подмножество
найдется подмножество 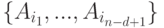 , состоящее из событий, от совокупности которых
, состоящее из событий, от совокупности которых  не зависит
не зависит
из множества 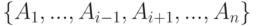 найдется подмножество
найдется подмножество 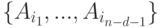 , состоящее из событий, от совокупности которых
, состоящее из событий, от совокупности которых  не зависит(Верный ответ)
не зависит(Верный ответ)
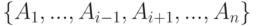 найдется подмножество
найдется подмножество 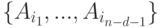 , состоящее из событий, от совокупности которых
, состоящее из событий, от совокупности которых  не зависит(Верный ответ)
не зависит(Верный ответ)

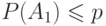 и любое событие
и любое событие  .Тогда ...
.Тогда ...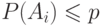 и любое событие
и любое событие  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком красная. При каком условии событие
целиком красная. При каком условии событие 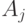 ?
? .Пусть
.Пусть 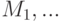
 -элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем
-элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем 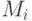 , тогда существует одноцветная раскраска данного
, тогда существует одноцветная раскраска данного  -вероятность покрасить ребро в красный цвет и
-вероятность покрасить ребро в красный цвет и  - вероятность покрасить ребро в синий цвет. Определим события
- вероятность покрасить ребро в синий цвет. Определим события 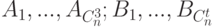 , где
, где 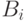 -состоит в том, что
-состоит в том, что  целиком синяя. Если для некоторого события
целиком синяя. Если для некоторого события  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Допустим,
. Допустим, 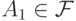 . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в 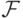 кроме
кроме  ?
?