Что согласно локальной леммы Ловаса является верным для событий, определенныx следующим образом? Пусть 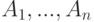 события, для каждого из которых выполнено
события, для каждого из которых выполнено 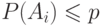 и любое событие
и любое событие  независит от остальных событий кроме не более чем
независит от остальных событий кроме не более чем  штук, причем и
штук, причем и  .Тогда ...
.Тогда ...
(Отметьте один правильный вариант ответа.)
Варианты ответа

 (Верный ответ)
(Верный ответ)


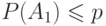 и любое событие
и любое событие  .Пусть
.Пусть 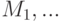
 -элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем
-элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем 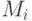 , тогда существует одноцветная раскраска данного
, тогда существует одноцветная раскраска данного 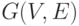 произвольный орграф зависимостей и существуют
произвольный орграф зависимостей и существуют  такие, что для любого
такие, что для любого  выполнено
выполнено 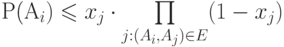 . Тогда ...
. Тогда ...  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Допустим,
. Допустим, 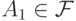 . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в 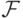 кроме
кроме  ?
?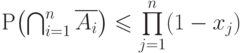 . Что верно относительно
. Что верно относительно  ?
? в графе
в графе  целиком красная. При каком условии событие
целиком красная. При каком условии событие 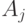 ?
?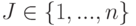 при выполнении некоторого ограничения на множество
при выполнении некоторого ограничения на множество 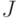 выполняется равенство
выполняется равенство  . Какое условие накладывается на множество
. Какое условие накладывается на множество