Пусть имеется простой граф  ,у которого
,у которого 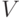 – множество вершин и
– множество вершин и  – множество ребер.
– множество ребер. хроматическое число графа и
хроматическое число графа и 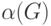 число независимости графа. Какое утверждение является верным?
число независимости графа. Какое утверждение является верным?
(Отметьте один правильный вариант ответа.)
Варианты ответа
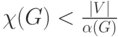
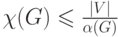
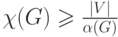 (Верный ответ)
(Верный ответ)
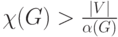

 число независимости и
число независимости и  кликовое число. Какое утверждение является верным?
кликовое число. Какое утверждение является верным?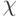 хроматическое число и
хроматическое число и  называется … если для любых
называется … если для любых 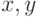 принадлежащих
принадлежащих 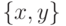 не принадлежит
не принадлежит  . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Допустим,
. Допустим, 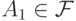 . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в 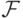 кроме
кроме  ?
?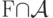 ?
?