База ответов ИНТУИТ

Дифференциальное исчисление функций одной переменной

<<- Назад к вопросам

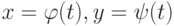Пусть функция y = f(x) задана параметрически: x = \varphi (t), y = \psi (t) . Каким условиям должна удовлетворять функция 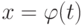x = \varphi (t) на интервале 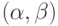(\alpha , \beta) для того, чтобы существовала производная y'_x:

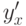(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
ограниченность
периодичность
монотонность(Верный ответ)
существование обратной функции(Верный ответ)
дифференцируемость(Верный ответ)
непрерывность(Верный ответ)
Похожие вопросы
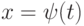Пусть функция y = f(x) задана параметрически: x = \varphi (t), y = \psi (t) . Каким условиям должна удовлетворять функция x = \psi (t) на интервале (\alpha , \beta) для того, чтобы существовала производная y'_x:
Пусть функция y = f(x) задана параметрически: x = \varphi (t), y = \psi (t) . Чему равна производная y'_x:
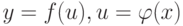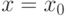Каким условиям должны удовлетворять функции y = f(u), u = \varphi (x) в точках u_0 = \varphi (x_0) и x = x_0 соответственно , чтобы сложная функция y = f[\varphi (x)] была дифференцируемой в точке x = x_0:
Каким условием должна удовлетворять функция y = f(x) для того, чтобы существовала непрерывная убывающая обратная функция x = \varphi (y):
Каким условием должна удовлетворять функция y = f(x) для того, чтобы существовала непрерывная возрастающая обратная функция x = \varphi (y):
Пусть x_0 - критическая точка f(x), но f(x) непрерывна в x_0. Тогда функция f(x) в точке x_0 имеет минимум, если её производная f'(x) при переходе через точку x_0
Пусть x_0 - критическая точка f(x), но f(x) непрерывна в x_0. Тогда функция f(x) в точке x_0 имеет максимум, если её производная f'(x) при переходе через точку x_0
Пусть x_0 - критическая точка f(x), но f(x) непрерывна в x_0. Тогда функция f(x) в точке x_0 имеет экстремум, если её производная f'(x) при переходе через точку x_0
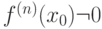Пусть для функции f(x) в окрестности точки x_0 существует производная n-го порядка, непрерывная в x_0 и f^{(n)}(x_0) \neg 0 - первая отличная от нуля производная. Тогда x_0 - точка максимума f(x), если
Пусть для функции f(x) в окрестности точки x_0 существует производная n-го порядка и f^{(n)}(x_0) \neg 0 - первая отличная от нуля производная. Тогда x_0 - не является точкой минимума и максимума f(x), если