Инвестиции - ответы
Даны пары значений  и
и  .
.
 | 10 | 29 | 13 | 30 | 24 | 59 | 12 | 34 | 30 |
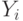 | 13 | 17 | 20 | 15 | 25 | 41 | 12 | 29 | 25 |
Если все значения  увеличить в 2 раза то коэффициент корреляции…
увеличить в 2 раза то коэффициент корреляции…
Будет ли выгоден бизнес, который приносил доходы в течение 3 лет в соответствии с таблицей (столбец D), при первоначальных затратах 15 у.е и учетной ставке 10%. На третий год бизнес был продан за 5 у.е.
| Год | Расход | Доход |
|---|---|---|
| 0 | 15 | 0 |
| 1 | 0 | 4 |
| 2 | 0 | 5 |
| 3 | 0 | 7+5 |
Даны пары значений  и
и  .
.
 | 12 | 24 | 16 | 27 | 28 | 67 | 18 | 26 | 38 |
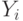 | 15 | 19 | 23 | 12 | 30 | 43 | 10 | 33 | 28 |
Найти коэффициенты уравнения регрессии:  .
.
Даны пары значений  и
и  .
.
 | 8 | 22 | 17 | 34 | 27 | 57 | 14 | 20 | 40 |
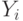 | 14 | 18 | 26 | 11 | 35 | 34 | 20 | 34 | 25 |
Найти остаточное среднее квадратичное отклонение.
Учетная ставка 5%. Ценная бумага куплена за 15 у.е., дивиденды за год составили 3 у.е.. Акция была продана за 40 у.е. через год. Каков доход (у.е.) от инвестирования в эту бумагу?
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 15%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -500 |
| 1 | 150 |
| 2 | 200 |
| 3 | 250 |
| 4 | 300 |
| 5 | -200 |
| 6 | 150 |
| 7 | 300 |
Номинал облигации 100 у.е., ежегодные выплаты составляют 8 у.е., учетная ставка 5%, срок обращения облигации 5 лет. Определите рыночную цену облигации. Ответ округлить до сотых.
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 5%. В ответе указать среднее квадратичное отклонение доходности портфеля. Ответ округлить до тысячных (три знака после запятой).
Номинал облигации 100 у.е., ежегодные выплаты составляют 8 у.е., учетная ставка 5%, срок обращения облигации 5 лет. Определите дюрацию облигации. Ответ округлить до сотых.
Номинал облигации 100 у.е., ежегодные выплаты составляют 8 у.е., учетная ставка ( ) меняется каждый год, как указано в таблице. Срок обращения облигации 8 лет. Определите дюрацию облигации. Ответ округлить до сотых.
) меняется каждый год, как указано в таблице. Срок обращения облигации 8 лет. Определите дюрацию облигации. Ответ округлить до сотых.
| Год |  (%) (%) |
|---|---|
| 1 | 5 |
| 2 | 4 |
| 3 | 6 |
| 4 | 7 |
| 5 | 8 |
| 6 | 4 |
| 7 | 7 |
| 8 | 9 |
Чему будет равен дисконт (в %) на 1 год при учетной ставке 17%? Ответ округлите до 1 знака после запятой.
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 9 | 8 | 6 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать минимально возможное среднее квадратичное отклонение доходности портфеля. (Ответ округлить до сотых.)
. В ответе указать минимально возможное среднее квадратичное отклонение доходности портфеля. (Ответ округлить до сотых.)
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 30%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -500 |
| 1 | 150 |
| 2 | 200 |
| 3 | 250 |
| 4 | 300 |
| 5 | -200 |
| 6 | 150 |
| 7 | 300 |
Номинал облигации 100 у.е., ежегодные выплаты составляют 4 у.е., учетная ставка 6%, срок обращения облигации 8 лет. Определите рыночную цену облигации. Ответ округлить до сотых.
Ценная бумага куплена за 20 у.е., дивиденды за год составили 2 у.е.. Акция была продана за 40 у.е. Какова доходность (%) инвестирования в эту бумагу?
Известна вероятность банкротства 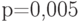 в течение года. Оцените количество лет за которые по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма менее одного.
в течение года. Оцените количество лет за которые по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма менее одного.
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 7 | 7 | 7 | 7 | 7 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 4. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 4. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 9 | 8 | 6 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать минимально возможную дисперсию портфеля. (Ответ округлить до сотых.)
. В ответе указать минимально возможную дисперсию портфеля. (Ответ округлить до сотых.)
Известна вероятность банкротства 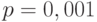 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.) 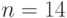 .
.
В таблице представлены доходности двух ценных бумаг в три периода времени. Вычислите дисперсию бумаги B. Ответ округлите до двух знаков после запятой.
 | 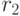 | 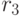 | |
|---|---|---|---|
| A | 4 | -1 | 2 |
| B | -2 | 5 | 10 |
Известна вероятность банкротства 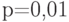 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за 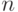 лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.) 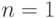 .
.
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать долю в портфеле бумаги номер 2. Ответ округлить до тысячных (три знака после запятой).
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | 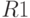 | 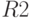 |  | 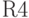 | 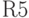 |
|---|---|---|---|---|---|
| 1 | 7 | 7 | 7 | 7 | 7 |
| 7 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 2.
. В ответе указать долю ценной бумаги № 2.
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 5%. В ответе указать дисперсию портфеля. Ответ округлить до тысячных (три знака после запятой).
Доходности ценных бумаг входящих в состав портфеля ( ), их доли в портфеле (
), их доли в портфеле ( ) и дисперсии доходности (
) и дисперсии доходности (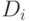 ) заданы в таблице. Ковариация доходностей равна 3.
) заданы в таблице. Ковариация доходностей равна 3.
 |  | 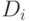 |
|---|---|---|
| 0,2 | 7 | 3 |
| 0,8 | 10 | 8 |
Найти доходность портфеля. Ответ введите с точностью до 2-го знака после запятой.
Учетная ставка 5%. Ценная бумага куплена по номинальной стоимости за 30 у.е., дивиденды через год составили 4 у.е.. Сколько должна стоить ценная бумага? Ответ округлите до ближайшего целого.
Средние доходности ценных бумаг входящих в состав портфеля ( ) и их доли в портфеле (
) и их доли в портфеле ( ) заданы в таблице.
) заданы в таблице.
 |  |
|---|---|
| 0,5 | 5 |
| 0,5 | 7 |
Найти доходность портфеля.
Имеются 2 ценные бумаги с доходностями  =30 и
=30 и 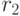 =10. Составить портфель ценных бумаг, обеспечивающий доходность 20%. В ответе указать долю в портфеле бумаги номер 1. Ответ введите с точностью до 1-го знака после запятой.
=10. Составить портфель ценных бумаг, обеспечивающий доходность 20%. В ответе указать долю в портфеле бумаги номер 1. Ответ введите с точностью до 1-го знака после запятой.
Учетная ставка 5%. Ценная бумага куплена по номинальной стоимости за 20 у.е., дивиденды через год составили 2 у.е.. Сколько должна стоить ценная бумага?
Учетная ставка 5%. Ценная бумага куплена за 30 у.е., дивиденды за год составили 4 у.е.. Акция была продана за 60 у.е. через год. Каков доход (у.е.) от инвестирования в эту бумагу?
Ценная бумага куплена за 15 у.е., дивиденды за год составили 3 у.е.. Акция была продана за 40 у.е. Какова доходность (%) инвестирования в эту бумагу? Ответ округлите до целого числа.
Учетная ставка 5%. Куплены три ценные бумаги по ценам (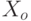 ), которые принесли дивиденды (
), которые принесли дивиденды (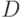 ).
).
 | 20 | 15 | 30 |
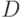 | 2 | 3 | 4 |
Каковы суммарные инвестиции?
Учетная ставка 5%. Куплены три ценные бумаги по ценам (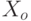 ), которые принесли дивиденды (
), которые принесли дивиденды ( ).
).
 | 20 | 15 | 30 |
 | 2 | 3 | 4 |
Каковы суммарные дивиденды?
Учетная ставка 5%, на депозит положено 5 000 000 рублей. Какая сумма будет на депозите через 3 года?
Какую сумму ежемесячно будет приносить вклад 100 000 рублей при учетной ставке 10% в год? Ответ округлите до целого числа.
Какой процент будет ежемесячно получать вкладчик при расчете по сложной формуле при годовой ставке 10%? Ответ укажите с точностью до шести знаков после запятой.
Каждый год на счет поступает 10 000 рублей при учетной ставке 10%. Сколько денег будет на счету через 3 года?
Чему будет равна стоимость актива, приносящего бесконечный ежегодный доход 5 000 при учетной ставке 15%? Ответ округлите до целого числа.
Чему равна эффективная ставка (в %) при учетной ставке 15% и инфляции 10%? Ответ укажите с точностью до одного знака после запятой.
Средства были инвестированы на 9 лет. Доходность от инвестирования (%) за каждый год приведена в таблице.
 | 2 |
 | 3 |
 | 4 |
 | 3 |
 | 5 |
 | 10 |
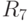 | 4 |
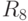 | 2 |
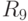 | 3 |
Какова средняя доходность за первые 2 года? (Ответ округлить до десятых.)
По оценкам экспертов ожидаемая доходность инвестиции может принять одно из значений  с вероятностями
с вероятностями  .
.
 |  |
| 8 | 0,1 |
| 10 | 0,1 |
| 12 | 0,15 |
| 14 | 0,15 |
| 16 | 0,2 |
| 18 | 0,15 |
| 20 | 0,1 |
| 22 | 0,05 |
Какова средняя доходность? (Средняя доходность вычисляется по формуле: ![r=\sum[r_i*P_i]](https://intuit.ru//sites/default/files/tex_cache/0e7fe0e9bd6c6c7a5e5883602eefcb12.png) . Ответ округлить до десятых.)
. Ответ округлить до десятых.)
По оценкам экспертов ожидаемая доходность инвестиции может принять одно из значений  с вероятностями
с вероятностями  .
.
 |  |
| 8 | 0,05 |
| 10 | 0,1 |
| 12 | 0,1 |
| 14 | 0,15 |
| 16 | 0,25 |
| 18 | 0,15 |
| 20 | 0,1 |
| 22 | 0,1 |
Какова дисперсия доходности? (Дисперсия вычисляется по формуле: ![D=\sum[P_i(M-R_i)^2]](https://intuit.ru//sites/default/files/tex_cache/dd01ba4e12c7847589985fa7dbafd7b2.png) .) Ответ округлить до сотых.
.) Ответ округлить до сотых.
По оценкам экспертов ожидаемая доходность инвестиции может принять одно из значений  с вероятностями
с вероятностями  .
.
 |  |
| 8 | 0,1 |
| 10 | 0,1 |
| 12 | 0,15 |
| 14 | 0,15 |
| 16 | 0,2 |
| 18 | 0,15 |
| 20 | 0,1 |
| 22 | 0,05 |
Каково среднее квадратичное отклонение доходности? Среднее квадратичное отклонение (сигма 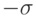 ) вычисляется по формуле:
) вычисляется по формуле: 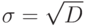 . Ответ округлить до сотых.
. Ответ округлить до сотых.
По оценкам экспертов ожидаемая доходность инвестиции может принять одно из значений  с вероятностями
с вероятностями  .
.
 |  |
| 8 | 0,1 |
| 10 | 0,1 |
| 12 | 0,15 |
| 14 | 0,15 |
| 16 | 0,2 |
| 18 | 0,15 |
| 20 | 0,1 |
| 22 | 0,05 |
Какова минимально возможная доходность по правилу трех сигм? Минимально возможная доходность по правилу трех сигм вычисляется по формуле:  . Ответ введите с точностью до 2-го знака после запятой.
. Ответ введите с точностью до 2-го знака после запятой.
По оценкам экспертов ожидаемая доходность инвестиции может принять одно из значений  с вероятностями
с вероятностями  .
.
 |  |
| 8 | 0,1 |
| 10 | 0,1 |
| 12 | 0,15 |
| 14 | 0,15 |
| 16 | 0,2 |
| 18 | 0,15 |
| 20 | 0,1 |
| 22 | 0,05 |
Какова максимально возможная доходность по правилу трех сигм? Максимально возможная доходность по правилу трех сигм вычисляется по формуле:  . Ответ введите с точностью до 2-го знака после запятой.
. Ответ введите с точностью до 2-го знака после запятой.
1000 рублей были вложены в две ценные бумаги. В ценную бумагу с доходностью  =7% было вложено 400 рублей, с доходностью
=7% было вложено 400 рублей, с доходностью 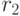 =5% - оставшиеся 600 рублей. Какова будет общая доходность (%)? Ответ округлите до десятых.
=5% - оставшиеся 600 рублей. Какова будет общая доходность (%)? Ответ округлите до десятых.
Деньги были вложены в три ценные бумаги в соответствии с таблицей, где D-дисперсия инструмента, r-доходность (в %). Рассчитайте дисперсию инвестиционного портфеля. Ответ округлите до сотых.
| 1 | 2 | 3 | |
|---|---|---|---|
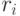 | 2 | 3 | 4 |
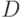 | 1 | 4 | 9 |
 | 0,3 | 0,3 | 0,4 |
В таблице представлены доходности двух ценных бумаг в три периода времени. Вычислите ковариацию между ними. Ответ округлите до двух знаков после запятой.
 | 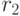 | 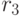 | |
|---|---|---|---|
| A | 1 | 2 | 4 |
| B | 2 | 4 | 3 |
В таблице представлены доходности двух ценных бумаг в три периода времени. Вычислите коэффициент линейной корреляции между ними. Ответ округлите до двух знаков после запятой.
 | 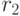 | 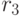 | |
|---|---|---|---|
| A | 4 | -1 | 2 |
| B | -2 | 5 | 10 |
В таблице представлены доходности двух ценных бумаг в три периода времени. Вычислите среднюю доходность бумаги A. Ответ округлите до двух знаков после запятой.
 | 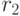 | 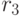 | |
|---|---|---|---|
| A | 1 | 2 | 4 |
| B | 2 | 4 | 3 |
Средние доходности ценных бумаг входящих в состав портфеля ( ) и их доли в портфеле (
) и их доли в портфеле ( ) заданы в таблице.
) заданы в таблице.
 |  |
|---|---|
| 0,6 | 5 |
| 0,4 | 7 |
Найти доходность портфеля.
Ответ введите с точностью до 1-го знака после запятой.Доходности ценных бумаг входящих в состав портфеля ( ), их доли в портфеле (
), их доли в портфеле ( ) и дисперсии доходности (
) и дисперсии доходности (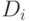 ) заданы в таблице. Ковариация доходностей равна 3.
) заданы в таблице. Ковариация доходностей равна 3.
 |  | 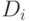 |
|---|---|---|
| 0,6 | 6 | 5 |
| 0,4 | 8 | 10 |
Найти дисперсию доходности портфеля. Ответ введите с точностью до 2-го знака после запятой.
Доходности ценных бумаг входящих в состав портфеля ( ), их доли в портфеле (
), их доли в портфеле ( ) и дисперсии доходности (
) и дисперсии доходности (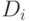 ) заданы в таблице. Ковариация доходностей равна 3.
) заданы в таблице. Ковариация доходностей равна 3.
 |  | 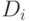 |
|---|---|---|
| 0,6 | 6 | 5 |
| 0,4 | 8 | 10 |
Найти среднее квадратичное отклонение доходности портфеля. Ответ введите с точностью до 2-го знака после запятой.
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать долю в портфеле бумаги номер 1. Ответ округлить до тысячных (три знака после запятой).
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 5%. В ответе указать долю в портфеле бумаги номер 2. Ответ округлить до тысячных (три знака после запятой).
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 5%. В ответе указать долю в портфеле бумаги номер 3. Ответ округлить до одного знака после запятой.
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать дисперсию портфеля. Ответ округлить до тысячных (три знака после запятой).
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 10%. В ответе указать среднее квадратичное отклонение доходности портфеля. Ответ округлить до тысячных (три знака после запятой).
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 5%. В ответе указать минимальную доходность портфеля (по правилу 3-х сигм). Ответ округлить до тысячных (три знака после запятой).
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 10%. В ответе указать максимальную доходность портфеля (по правилу 3-х сигм). Ответ округлить до тысячных (три знака после запятой).
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать долю в портфеле бумаги номер 1. Ответ округлить до тысячных (три знака после запятой).
Имеются 2 ценные бумаги с доходностями  =20 и
=20 и 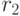 =5. Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать долю в портфеле бумаги номер 2. Ответ введите с точностью до 2-го знака после запятой.
=5. Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать долю в портфеле бумаги номер 2. Ответ введите с точностью до 2-го знака после запятой.
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 9 | 8 | 6 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 1. ( Ответ введите с точностью до 2-го знака после запятой.)
. В ответе указать долю ценной бумаги № 1. ( Ответ введите с точностью до 2-го знака после запятой.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 9 | 8 | 6 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 2. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 2. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 8 | 4 | 15 |
| 2 | 3 | 6 | 9 | 6 | 17 |
| 3 | 4 | 7 | 11 | 8 | 16 |
| 4 | 5 | 8 | 9 | 4 | 18 |
| 5 | 4 | 9 | 12 | 6 | 12 |
| 6 | 3 | 7 | 10 | 5 | 9 |
| 7 | 4 | 8 | 9 | 7 | 8 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 3. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 3. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 9 | 8 | 6 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 4. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 4. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 8 | 4 | 15 |
| 2 | 3 | 6 | 9 | 6 | 17 |
| 3 | 4 | 7 | 11 | 8 | 16 |
| 4 | 5 | 8 | 9 | 4 | 18 |
| 5 | 4 | 9 | 12 | 6 | 12 |
| 6 | 3 | 7 | 10 | 5 | 9 |
| 7 | 4 | 8 | 9 | 7 | 8 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 5. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 5. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 8 | 4 | 15 |
| 2 | 3 | 6 | 9 | 6 | 17 |
| 3 | 4 | 7 | 11 | 8 | 16 |
| 4 | 5 | 8 | 9 | 4 | 18 |
| 5 | 4 | 9 | 12 | 6 | 12 |
| 6 | 3 | 7 | 10 | 5 | 9 |
| 7 | 4 | 8 | 9 | 7 | 8 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать дисперсию портфеля. (Ответ округлить до сотых.)
. В ответе указать дисперсию портфеля. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 7 | 7 | 7 | 7 | 7 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать минимально возможное среднее квадратичное отклонение доходности портфеля. (Ответ округлить до сотых.)
. В ответе указать минимально возможное среднее квадратичное отклонение доходности портфеля. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | 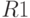 | 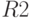 |  | 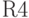 | 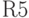 |
|---|---|---|---|---|---|
| 1 | 7 | 7 | 7 | 7 | 7 |
| 7 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 1. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 1. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | R_1 | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 8 | 4 | 15 |
| 2 | 3 | 6 | 9 | 6 | 17 |
| 3 | 4 | 7 | 11 | 8 | 16 |
| 4 | 5 | 8 | 9 | 4 | 18 |
| 5 | 4 | 9 | 12 | 6 | 12 |
| 6 | 3 | 7 | 10 | 5 | 9 |
| 7 | 4 | 8 | 9 | 7 | 8 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 3. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 3. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | 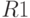 | 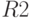 |  | 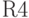 | 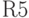 |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 8 | 4 | 15 |
| 2 | 3 | 6 | 9 | 6 | 17 |
| 3 | 4 | 7 | 11 | 8 | 16 |
| 4 | 5 | 8 | 9 | 4 | 18 |
| 5 | 4 | 9 | 12 | 6 | 12 |
| 6 | 3 | 7 | 10 | 5 | 9 |
| 7 | 4 | 8 | 9 | 7 | 8 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 4. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 4. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | 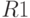 | 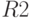 |  | 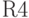 | 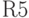 |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 9 | 8 | 6 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 5. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 5. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | 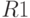 | 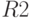 |  | 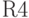 | 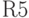 |
|---|---|---|---|---|---|
| 1 | 7 | 7 | 7 | 7 | 7 |
| 7 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать минимально возможную дисперсию портфеля. (Ответ округлить до сотых.)
. В ответе указать минимально возможную дисперсию портфеля. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | R_1 | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 8 | 4 | 15 |
| 2 | 3 | 6 | 9 | 6 | 17 |
| 3 | 4 | 7 | 11 | 8 | 16 |
| 4 | 5 | 8 | 9 | 4 | 18 |
| 5 | 4 | 9 | 12 | 6 | 12 |
| 6 | 3 | 7 | 10 | 5 | 9 |
| 7 | 4 | 8 | 9 | 7 | 8 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать минимально возможное среднее квадратичное отклонение доходности портфеля. (Ответ округлить до сотых.)
. В ответе указать минимально возможное среднее квадратичное отклонение доходности портфеля. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | 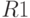 | 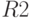 |  | 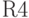 | 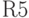 |
|---|---|---|---|---|---|
| 1 | 7 | 7 | 7 | 7 | 7 |
| 7 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать минимальную оценку доходности портфеля по правилу трех сигм. (Ответ округлить до сотых.)
. В ответе указать минимальную оценку доходности портфеля по правилу трех сигм. (Ответ округлить до сотых.)
Номинал облигации 100 у.е., ежегодные выплаты составляют 9 у.е., учетная ставка 7%, срок обращения облигации 5 лет. Определите дюрацию облигации. Ответ округлить до сотых.
Номинал облигации 100 у.е., ежегодные выплаты составляют 9 у.е., учетная ставка 7%, срок обращения облигации 8 лет. Определите рыночную цену облигации. Ответ округлить до сотых.
Номинал облигации 100 у.е., ежегодные выплаты составляют 8 у.е., учетная ставка 5%, срок обращения облигации 8 лет. Определите дюрацию облигации. Ответ округлить до сотых.
Номинал облигации 100 у.е., ежегодные выплаты составляют 4 у.е., учетная ставка ( ) меняется каждый год, как указано в таблице. Срок обращения облигации 5 лет. Определите рыночную цену облигации. Ответ округлить до сотых.
) меняется каждый год, как указано в таблице. Срок обращения облигации 5 лет. Определите рыночную цену облигации. Ответ округлить до сотых.
| Год |  (%) (%) |
|---|---|
| 1 | 4 |
| 2 | 7 |
| 3 | 6 |
| 4 | 9 |
| 5 | 8 |
Номинал облигации 100 у.е., ежегодные выплаты составляют 9 у.е., учетная ставка ( ) меняется каждый год, как указано в таблице. Срок обращения облигации 5 лет. Определите дюрацию облигации. Ответ округлить до сотых.
) меняется каждый год, как указано в таблице. Срок обращения облигации 5 лет. Определите дюрацию облигации. Ответ округлить до сотых.
| Год |  (%) (%) |
|---|---|
| 1 | 4 |
| 2 | 5 |
| 3 | 10 |
| 4 | 8 |
| 5 | 4 |
Номинал облигации 100 у.е., ежегодные выплаты составляют 8 у.е., учетная ставка ( ) меняется каждый год, как указано в таблице. Срок обращения облигации 8 лет. Определите рыночную цену облигации. Ответ округлить до сотых.
) меняется каждый год, как указано в таблице. Срок обращения облигации 8 лет. Определите рыночную цену облигации. Ответ округлить до сотых.
| Год |  (%) (%) |
|---|---|
| 1 | 5 |
| 2 | 4 |
| 3 | 6 |
| 4 | 7 |
| 5 | 8 |
| 6 | 4 |
| 7 | 7 |
| 8 | 9 |
Номинал облигации 100 у.е., ежегодные выплаты составляют 4 у.е., учетная ставка ( ) меняется каждый год, как указано в таблице. Срок обращения облигации 8 лет. Определите дюрацию облигации. Ответ округлить до сотых.
) меняется каждый год, как указано в таблице. Срок обращения облигации 8 лет. Определите дюрацию облигации. Ответ округлить до сотых.
| Год |  (%) (%) |
|---|---|
| 1 | 4 |
| 2 | 7 |
| 3 | 6 |
| 4 | 9 |
| 5 | 8 |
| 6 | 5 |
| 7 | 6 |
| 8 | 7 |
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 5%. Ответ округлить до ближайшего целого.
| Год | Поток |
|---|---|
| 0 | -500 |
| 1 | 150 |
| 2 | 200 |
| 3 | 250 |
| 4 | 300 |
| 5 | -200 |
| 6 | 150 |
| 7 | 300 |
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 10%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -500 |
| 1 | 150 |
| 2 | 200 |
| 3 | 250 |
| 4 | 300 |
| 5 | -200 |
| 6 | 150 |
| 7 | 300 |
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 20%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -200 |
| 1 | 50 |
| 2 | 100 |
| 3 | 120 |
| 4 | 150 |
| 5 | -50 |
| 6 | 200 |
| 7 | 300 |
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 25%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -200 |
| 1 | 50 |
| 2 | 100 |
| 3 | 120 |
| 4 | 150 |
| 5 | -50 |
| 6 | 200 |
| 7 | 300 |
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 30%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -300 |
| 1 | 150 |
| 2 | 100 |
| 3 | 180 |
| 4 | -150 |
| 5 | -50 |
| 6 | 300 |
| 7 | 200 |
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 35%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -300 |
| 1 | 150 |
| 2 | 100 |
| 3 | 180 |
| 4 | -150 |
| 5 | -50 |
| 6 | 300 |
| 7 | 200 |
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить доходность инвестиций в проект с точностью до 1%. Ответ округлить до целых.
| Год | Поток |
|---|---|
| 0 | -500 |
| 1 | 150 |
| 2 | 200 |
| 3 | 250 |
| 4 | 300 |
| 5 | -200 |
| 6 | 150 |
| 7 | 300 |
Известна вероятность банкротства 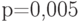 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.)  .
.
Известна вероятность банкротства 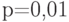 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.)  .
.
Известна вероятность банкротства 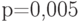 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.)  .
.
Известна вероятность банкротства 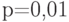 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до одного знака после запятой.)
лет. (Ответ округлить до одного знака после запятой.)  .
.
Известна вероятность банкротства 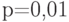 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за 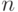 лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.) 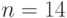 .
.
Известна вероятность банкротства 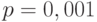 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до одного знака после запятой.)
лет. (Ответ округлить до одного знака после запятой.) 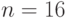 .
.
Эксперта привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Оцените среднюю ошибку эксперта. Ответ введите с точностью до 2-го знака после запятой.
| Оценка эксперта | 3 | 5 | 7 | 4 |
| Реальное значение | 4 | 2 | 4 | 8 |
Эксперта привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Оцените ошибку эксперта при втором измерении.
| Оценка эксперта | 3 | 5 | 7 | 4 |
| Реальное значение | 4 | 2 | 4 | 8 |
Экспертов привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Оцените, какой из экспертов ошибался в своих оценках меньше всех. В ответе укажите номер эксперта.
| Оценка эксперта 1 | 5 | 7 | 9 | 7 |
| Оценка эксперта 2 | 4 | 3 | 2 | 5 |
| Оценка эксперта 3 | 3 | 1 | 5 | 9 |
| Оценка эксперта 4 | 5 | 7 | 5 | 8 |
| Оценка эксперта 5 | 3 | 4 | 4 | 8 |
| Реальное значение | 4 | 2 | 4 | 8 |
Экспертов привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Оцените, какой из экспертов ошибался в своих оценках больше всех. В ответе укажите номер эксперта.
| Оценка эксперта 1 | 3 | 5 | 4 | 5 |
| Оценка эксперта 2 | 5 | 3 | 3 | 5 |
| Оценка эксперта 3 | 4 | 3 | 5 | 9 |
| Оценка эксперта 4 | 5 | 6 | 5 | 8 |
| Оценка эксперта 5 | 7 | 3 | 7 | 6 |
| Реальное значение | 6 | 4 | 5 | 8 |
Экспертов привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Найдите вес 3-го эксперта. Ответ введите с точностью до 1-го знака после запятой.
| Оценка эксперта 1 | 3 | 5 | 4 | 5 |
| Оценка эксперта 2 | 5 | 3 | 3 | 5 |
| Оценка эксперта 3 | 4 | 3 | 5 | 9 |
| Оценка эксперта 4 | 5 | 6 | 5 | 8 |
| Оценка эксперта 5 | 7 | 3 | 7 | 6 |
| Реальное значение | 6 | 4 | 5 | 8 |
Экспертов привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Найдите вес 2-го эксперта. Ответ округлите до сотых.
| Оценка эксперта 1 | 3 | 5 | 4 | 5 |
| Оценка эксперта 2 | 5 | 3 | 3 | 5 |
| Оценка эксперта 3 | 4 | 3 | 5 | 9 |
| Оценка эксперта 4 | 5 | 6 | 5 | 8 |
| Оценка эксперта 5 | 3 | 4 | 4 | 8 |
| Реальное значение | 6 | 4 | 5 | 8 |
Экспертов привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Найдите сумму весов экспертов. Ответ округлите до сотых.
| Оценка эксперта 1 | 3 | 5 | 4 | 5 |
| Оценка эксперта 2 | 5 | 3 | 3 | 5 |
| Оценка эксперта 3 | 4 | 3 | 5 | 9 |
| Оценка эксперта 4 | 5 | 6 | 5 | 8 |
| Оценка эксперта 5 | 7 | 3 | 7 | 6 |
| Реальное значение | 6 | 4 | 5 | 8 |
Экспертов привлекали 5 раз для прогноза доходности инвестиционного проекта. Реальная доходность проекта в 4-х случаях уже известна. Оцените возможное реальное значение в пятом случае, если известны оценки экспертов. Ответ округлите до сотых.
| Оценка эксперта 1 | 5 | 7 | 9 | 7 | 6 |
| Оценка эксперта 2 | 4 | 3 | 2 | 5 | 5 |
| Оценка эксперта 3 | 3 | 1 | 5 | 9 | 4 |
| Оценка эксперта 4 | 5 | 7 | 5 | 8 | 6 |
| Оценка эксперта 5 | 3 | 4 | 4 | 8 | 4 |
| Реальное значение | 4 | 2 | 4 | 8 | ? |
По оценкам экспертов ожидаемая доходность инвестиции может принять одно из значений  с вероятностями
с вероятностями  .
.
 |  |
| 8 | 0,05 |
| 10 | 0,1 |
| 12 | 0,1 |
| 14 | 0,15 |
| 16 | 0,25 |
| 18 | 0,15 |
| 20 | 0,1 |
| 22 | 0,1 |
Какова минимально возможная доходность по правилу трех сигм? Минимально возможная доходность по правилу трех сигм вычисляется по формуле:  . Ответ введите с точностью до 2-го знака после запятой.
. Ответ введите с точностью до 2-го знака после запятой.
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 20%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -500 |
| 1 | 150 |
| 2 | 200 |
| 3 | 250 |
| 4 | 300 |
| 5 | -200 |
| 6 | 150 |
| 7 | 300 |
По оценкам экспертов ожидаемая доходность инвестиции может принять одно из значений  с вероятностями
с вероятностями  .
.
 |  |
| 8 | 0,1 |
| 10 | 0,15 |
| 12 | 0,1 |
| 14 | 0,2 |
| 16 | 0,3 |
| 18 | 0,1 |
| 20 | 0,1 |
| 22 | 0,05 |
Какова максимально возможная доходность по правилу трех сигм? Максимально возможная доходность по правилу трех сигм вычисляется по формуле:  . Ответ введите с точностью до 2-го знака после запятой.
. Ответ введите с точностью до 2-го знака после запятой.
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 25%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -500 |
| 1 | 150 |
| 2 | 200 |
| 3 | 250 |
| 4 | 300 |
| 5 | -200 |
| 6 | 150 |
| 7 | 300 |
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 35%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -200 |
| 1 | 50 |
| 2 | 100 |
| 3 | 120 |
| 4 | 150 |
| 5 | -50 |
| 6 | 200 |
| 7 | 300 |
По оценкам экспертов ожидаемая доходность инвестиции может принять одно из значений  с вероятностями
с вероятностями  .
.
 |  |
| 8 | 0,1 |
| 10 | 0,1 |
| 12 | 0,15 |
| 14 | 0,15 |
| 16 | 0,2 |
| 18 | 0,15 |
| 20 | 0,1 |
| 22 | 0,05 |
Какова дисперсия доходности? (Дисперсия вычисляется по формуле: ![D=\sum[P_i(M-R_i)^2]](https://intuit.ru//sites/default/files/tex_cache/dd01ba4e12c7847589985fa7dbafd7b2.png) .) Ответ округлить до сотых.
.) Ответ округлить до сотых.
Каждый год на счет поступает 15 000 рублей при учетной ставке 10%. Сколько денег будет на счету через 4 года?
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 7 | 7 | 7 | 7 | 7 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 5. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 5. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | 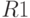 | 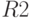 |  | 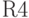 | 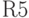 |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 8 | 4 | 15 |
| 2 | 3 | 6 | 9 | 6 | 17 |
| 3 | 4 | 7 | 11 | 8 | 16 |
| 4 | 5 | 8 | 9 | 4 | 18 |
| 5 | 4 | 9 | 12 | 6 | 12 |
| 6 | 3 | 7 | 10 | 5 | 9 |
| 7 | 4 | 8 | 9 | 7 | 8 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 5. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 5. (Ответ округлить до сотых.)
Эксперта привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Оцените ошибку эксперта при втором измерении.
| Оценка эксперта | 5 | 6 | 4 | 7 |
| Реальное значение | 4 | 5 | 4 | 7 |
Учетная ставка 5%. Куплены три ценные бумаги по ценам (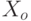 ), которые принесли дивиденды (
), которые принесли дивиденды ( ).
).
 | 20 | 15 | 30 |
 | 1 | 3 | 4 |
Каковы суммарные дивиденды?
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | 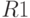 | 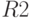 |  | 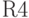 | 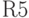 |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 9 | 8 | 6 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 3. (Ответ введите с точностью до 1-го знака после запятой.)
. В ответе указать долю ценной бумаги № 3. (Ответ введите с точностью до 1-го знака после запятой.)
Экспертов привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Найдите вес 3-го эксперта. Ответ введите с точностью до 1-го знака после запятой.
| Оценка эксперта 1 | 3 | 5 | 4 | 5 |
| Оценка эксперта 2 | 5 | 3 | 3 | 5 |
| Оценка эксперта 3 | 4 | 3 | 5 | 9 |
| Оценка эксперта 4 | 5 | 6 | 5 | 8 |
| Оценка эксперта 5 | 3 | 4 | 4 | 8 |
| Реальное значение | 6 | 4 | 5 | 8 |
1000 рублей были вложены в две ценные бумаги. В ценную бумагу с доходностью  =20% было вложено 800 рублей, с доходностью
=20% было вложено 800 рублей, с доходностью 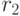 =5% - оставшиеся 200 рублей. Какова будет общая доходность (%)?
=5% - оставшиеся 200 рублей. Какова будет общая доходность (%)?
Учетная ставка 5%. Куплены три ценные бумаги по ценам (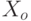 ), которые принесли дивиденды (
), которые принесли дивиденды ( ).
).
 | 10 | 15 | 10 |
 | 2 | 3 | 4 |
Каковы суммарные инвестиции?
Средние доходности ценных бумаг входящих в состав портфеля ( ) и их доли в портфеле (
) и их доли в портфеле ( ) заданы в таблице.
) заданы в таблице.
 |  |
|---|---|
| 0,3 | 5 |
| 0,7 | 7 |
Найти доходность портфеля. Ответ введите с точностью до 1-го знака после запятой.
Даны пары значений  и
и  .
.
 | 8 | 22 | 17 | 34 | 27 | 57 | 14 | 20 | 40 |
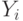 | 14 | 18 | 26 | 11 | 35 | 34 | 20 | 34 | 25 |
Если все значения  увеличить в 2 раза то коэффициент
увеличить в 2 раза то коэффициент  в уравнении регрессии
в уравнении регрессии  …
…
Экспертов привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Найдите вес 2-го эксперта. Ответ введите с точностью до 2-го знака после запятой.
| Оценка эксперта 1 | 3 | 5 | 4 | 5 |
| Оценка эксперта 2 | 5 | 3 | 3 | 5 |
| Оценка эксперта 3 | 4 | 3 | 5 | 9 |
| Оценка эксперта 4 | 5 | 6 | 5 | 8 |
| Оценка эксперта 5 | 7 | 3 | 7 | 6 |
| Реальное значение | 6 | 4 | 5 | 8 |
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | 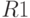 | 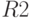 |  | 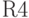 | 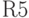 |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 9 | 8 | 6 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать минимально возможное среднее квадратичное отклонение доходности портфеля. (Ответ округлить до сотых.)
. В ответе указать минимально возможное среднее квадратичное отклонение доходности портфеля. (Ответ округлить до сотых.)
Известна вероятность банкротства 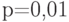 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.) 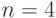 .
.
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 15%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -200 |
| 1 | 50 |
| 2 | 100 |
| 3 | 120 |
| 4 | 150 |
| 5 | -50 |
| 6 | 200 |
| 7 | 300 |
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | 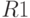 | 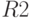 |  | 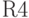 | 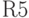 |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 9 | 8 | 6 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать минимальную оценку доходности портфеля по правилу трех сигм. (Ответ округлить до десятых.)
. В ответе указать минимальную оценку доходности портфеля по правилу трех сигм. (Ответ округлить до десятых.)
Будет ли выгоден бизнес, который приносил доходы в течение 3 лет в соответствии с таблицей (столбец D), при первоначальных затратах 5 у.е и учетной ставке 10%. На третий год бизнес был продан за 3 у.е.
| Год | Расход | Доход |
|---|---|---|
| 0 | 5 | 0 |
| 1 | 0 | 7 |
| 2 | 0 | 10 |
| 3 | 0 | 12+3 |
Учетная ставка 5%. Ценная бумага куплена по номинальной стоимости за 15 у.е., дивиденды через год составили 3 у.е.. Сколько должна стоить ценная бумага?
Учетная ставка 5%. Куплены три ценные бумаги по ценам (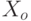 ), которые принесли дивиденды (
), которые принесли дивиденды ( ).
).
 | 15 | 15 | 30 |
 | 2 | 3 | 4 |
Каковы суммарные инвестиции?
Какую сумму ежемесячно будет приносить вклад 100 000 рублей при учетной ставке 5% в год? Ответ округлите до целого числа.
Каждый год на счет поступает 20 000 рублей при учетной ставке 5%. Сколько денег будет на счету через 2 года?
Чему будет равна стоимость актива, приносящего бесконечный ежегодный доход 10 000 при учетной ставке 5%?
Будет ли выгоден бизнес, который приносил доходы в течение 3 лет в соответствии с таблицей (столбец D), при первоначальных затратах 10 у.е и учетной ставке 50%. На третий год бизнес был продан за 5 у.е.
| Год | Расход | Доход |
|---|---|---|
| 0 | 10 | 0 |
| 1 | 0 | 5 |
| 2 | 0 | 7 |
| 3 | 0 | 7+5 |
Чему равна эффективная ставка (в %) при учетной ставке 10% и инфляции 15%? Ответ укажите с точностью до одного знака после запятой.
По оценкам экспертов ожидаемая доходность инвестиции может принять одно из значений  с вероятностями
с вероятностями  .
.
 |  |
| 8 | 0,05 |
| 10 | 0,1 |
| 12 | 0,1 |
| 14 | 0,15 |
| 16 | 0,25 |
| 18 | 0,15 |
| 20 | 0,1 |
| 22 | 0,1 |
Каково среднее квадратичное отклонение доходности? Среднее квадратичное отклонение (сигма -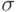 ) вычисляется по формуле:
) вычисляется по формуле: 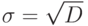 . Ответ округлить до сотых.
. Ответ округлить до сотых.
По оценкам экспертов ожидаемая доходность инвестиции может принять одно из значений  с вероятностями
с вероятностями  .
.
 |  |
| 8 | 0,05 |
| 10 | 0,1 |
| 12 | 0,1 |
| 14 | 0,15 |
| 16 | 0,25 |
| 18 | 0,15 |
| 20 | 0,1 |
| 22 | 0,1 |
Какова максимально возможная доходность по правилу трех сигм? Максимально возможная доходность по правилу трех сигм вычисляется по формуле:  . Ответ введите с точностью до 2-го знака после запятой.
. Ответ введите с точностью до 2-го знака после запятой.
1000 рублей были вложены в две ценные бумаги. В ценную бумагу с доходностью  =10% было вложено 600 рублей, с доходностью
=10% было вложено 600 рублей, с доходностью 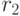 =15% - оставшиеся 400 рублей. Какова будет общая доходность (%)?
=15% - оставшиеся 400 рублей. Какова будет общая доходность (%)?
В таблице представлены доходности двух ценных бумаг в три периода времени. Вычислите дисперсию бумаги A. Ответ округлите до двух знаков после запятой.
 | 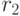 | 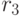 | |
|---|---|---|---|
| A | 1 | 2 | 4 |
| B | 2 | 4 | 3 |
В таблице представлены доходности двух ценных бумаг в три периода времени. Вычислите среднюю доходность бумаги B. Ответ округлите до двух знаков после запятой.
 | 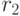 | 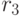 | |
|---|---|---|---|
| A | 4 | -1 | 2 |
| B | -2 | 5 | 10 |
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать долю в портфеле бумаги номер 3. Ответ округлить до тысячных (три знака после запятой).
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 10%. В ответе указать минимальную доходность портфеля (по правилу 3-х сигм). Ответ введите с точностью до 2-го знака после запятой.
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 8 | 4 | 15 |
| 2 | 3 | 6 | 9 | 6 | 17 |
| 3 | 4 | 7 | 11 | 8 | 16 |
| 4 | 5 | 8 | 9 | 4 | 18 |
| 5 | 4 | 9 | 12 | 6 | 12 |
| 6 | 3 | 7 | 10 | 5 | 9 |
| 7 | 4 | 8 | 9 | 7 | 8 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 1. ( Ответ введите с точностью до 1-го знака после запятой.)
. В ответе указать долю ценной бумаги № 1. ( Ответ введите с точностью до 1-го знака после запятой.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 8 | 4 | 15 |
| 2 | 3 | 6 | 9 | 6 | 17 |
| 3 | 4 | 7 | 11 | 8 | 16 |
| 4 | 5 | 8 | 9 | 4 | 18 |
| 5 | 4 | 9 | 12 | 6 | 12 |
| 6 | 3 | 7 | 10 | 5 | 9 |
| 7 | 4 | 8 | 9 | 7 | 8 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 2. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 2. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 7 | 7 | 7 | 7 | 7 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 3. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 3. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 9 | 8 | 6 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 5. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 5. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 9 | 8 | 6 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать минимально возможную дисперсию портфеля. (Ответ округлить до сотых.)
. В ответе указать минимально возможную дисперсию портфеля. (Ответ округлить до сотых.)
Даны пары значений  и
и  .
.
 | 10 | 29 | 13 | 30 | 24 | 59 | 12 | 34 | 30 |
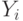 | 13 | 17 | 20 | 15 | 25 | 41 | 12 | 29 | 25 |
Найти коэффициенты уравнения регрессии:  .
.
Даны пары значений  и
и  .
.
 | 10 | 29 | 13 | 30 | 24 | 59 | 12 | 34 | 30 |
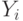 | 13 | 17 | 20 | 15 | 25 | 41 | 12 | 29 | 25 |
Найти остаточное среднее квадратичное отклонение.
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | 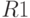 | 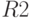 |  | 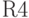 | 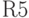 |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 9 | 8 | 6 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 4. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 4. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | 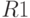 | 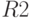 |  | 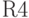 | 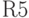 |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 9 | 8 | 6 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать минимально возможную дисперсию портфеля. (Ответ округлить до десятых.)
. В ответе указать минимально возможную дисперсию портфеля. (Ответ округлить до десятых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | 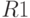 | 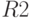 |  | 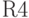 | 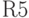 |
|---|---|---|---|---|---|
| 1 | 7 | 7 | 7 | 7 | 7 |
| 7 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать минимально возможное среднее квадратичное отклонение доходности портфеля. (Ответ округлить до сотых.)
. В ответе указать минимально возможное среднее квадратичное отклонение доходности портфеля. (Ответ округлить до сотых.)
Номинал облигации 100 у.е., ежегодные выплаты составляют 9 у.е., учетная ставка 7%, срок обращения облигации 5 лет. Определите рыночную цену облигации. Ответ округлить до сотых.
Номинал облигации 100 у.е., ежегодные выплаты составляют 8 у.е., учетная ставка 5%, срок обращения облигации 8 лет. Определите рыночную цену облигации. Ответ округлить до сотых.
Номинал облигации 100 у.е., ежегодные выплаты составляют 4 у.е., учетная ставка 6%, срок обращения облигации 8 лет. Определите дюрацию облигации. Ответ округлить до сотых.
Номинал облигации 100 у.е., ежегодные выплаты составляют 8 у.е., учетная ставка ( ) меняется каждый год, как указано в таблице. Срок обращения облигации 5 лет. Определите дюрацию облигации. Ответ округлить до сотых.
) меняется каждый год, как указано в таблице. Срок обращения облигации 5 лет. Определите дюрацию облигации. Ответ округлить до сотых.
| Год |  (%) (%) |
|---|---|
| 1 | 5 |
| 2 | 4 |
| 3 | 6 |
| 4 | 7 |
| 5 | 8 |
Номинал облигации 100 у.е., ежегодные выплаты составляют 9 у.е., учетная ставка ( ) меняется каждый год, как указано в таблице. Срок обращения облигации 8 лет. Определите дюрацию облигации. Ответ округлить до сотых.
) меняется каждый год, как указано в таблице. Срок обращения облигации 8 лет. Определите дюрацию облигации. Ответ округлить до сотых.
| Год |  (%) (%) |
|---|---|
| 1 | 7 |
| 2 | 8 |
| 3 | 2 |
| 4 | 4 |
| 5 | 3 |
| 6 | 4 |
| 7 | 8 |
| 8 | 8 |
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 5%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -200 |
| 1 | 50 |
| 2 | 100 |
| 3 | 120 |
| 4 | 150 |
| 5 | -50 |
| 6 | 200 |
| 7 | 300 |
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 20%. Ответ округлить до ближайшего целого.
| Год | Поток |
|---|---|
| 0 | -300 |
| 1 | 150 |
| 2 | 100 |
| 3 | 180 |
| 4 | -150 |
| 5 | -50 |
| 6 | 300 |
| 7 | 200 |
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 25%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -300 |
| 1 | 150 |
| 2 | 100 |
| 3 | 180 |
| 4 | -150 |
| 5 | -50 |
| 6 | 300 |
| 7 | 200 |
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 30%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -200 |
| 1 | 50 |
| 2 | 100 |
| 3 | 120 |
| 4 | 150 |
| 5 | -50 |
| 6 | 200 |
| 7 | 300 |
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить доходность инвестиций в проект с точностью до 1%. Ответ округлить до целых.
| Год | Поток |
|---|---|
| 0 | -300 |
| 1 | 150 |
| 2 | 100 |
| 3 | 180 |
| 4 | -150 |
| 5 | -50 |
| 6 | 300 |
| 7 | 200 |
Известна вероятность банкротства 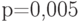 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.)  .
.
Известна вероятность банкротства 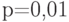 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.)  .
.
Известна вероятность банкротства 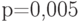 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.)  .
.
Известна вероятность банкротства 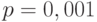 в течение года. Оцените количество лет за которые по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма менее одного.
в течение года. Оцените количество лет за которые по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма менее одного.
Эксперта привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Оцените среднюю ошибку эксперта. Ответ введите с точностью до 1-го знака после запятой.
| Оценка эксперта | 5 | 6 | 4 | 7 |
| Реальное значение | 4 | 5 | 4 | 7 |
Эксперта привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Оцените ошибку эксперта при втором измерении.
| Оценка эксперта | 5 | 7 | 9 | 7 |
| Реальное значение | 4 | 2 | 4 | 8 |
Экспертов привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Оцените, какой из экспертов ошибался в своих оценках меньше всех. В ответе укажите номер эксперта.
| Оценка эксперта 1 | 3 | 5 | 4 | 5 |
| Оценка эксперта 2 | 5 | 3 | 3 | 5 |
| Оценка эксперта 3 | 4 | 3 | 5 | 9 |
| Оценка эксперта 4 | 5 | 6 | 5 | 8 |
| Оценка эксперта 5 | 3 | 4 | 4 | 8 |
| Реальное значение | 6 | 4 | 5 | 8 |
Экспертов привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Оцените, какой из экспертов ошибался в своих оценках больше всех. В ответе укажите номер эксперта.
| Оценка эксперта 1 | 3 | 5 | 4 | 5 |
| Оценка эксперта 2 | 5 | 3 | 3 | 5 |
| Оценка эксперта 3 | 4 | 3 | 5 | 9 |
| Оценка эксперта 4 | 5 | 6 | 5 | 8 |
| Оценка эксперта 5 | 3 | 4 | 4 | 8 |
| Реальное значение | 6 | 4 | 5 | 8 |
Экспертов привлекали 5 раз для прогноза доходности инвестиционного проекта. Реальная доходность проекта в 4-х случаях уже известна. Оцените возможное реальное значение в пятом случае, если известны оценки экспертов. Ответ округлите до целого.
| Оценка эксперта 1 | 3 | 5 | 4 | 5 | 4 |
| Оценка эксперта 2 | 5 | 3 | 3 | 5 | 7 |
| Оценка эксперта 3 | 4 | 3 | 5 | 9 | 5 |
| Оценка эксперта 4 | 5 | 6 | 5 | 8 | 3 |
| Оценка эксперта 5 | 3 | 4 | 4 | 8 | 4 |
| Реальное значение | 6 | 4 | 5 | 8 | ? |
Какой процент будет ежемесячно получать вкладчик при расчете по сложной формуле при годовой ставке 5%? Ответ укажите с точностью до шести знаков после запятой.
По оценкам экспертов ожидаемая доходность инвестиции может принять одно из значений  с вероятностями
с вероятностями  .
.
 |  |
| 8 | 0,1 |
| 10 | 0,05 |
| 12 | 0,1 |
| 14 | 0,2 |
| 16 | 0,3 |
| 18 | 0,1 |
| 20 | 0,1 |
| 22 | 0,05 |
Какова минимально возможная доходность по правилу трех сигм? Минимально возможная доходность по правилу трех сигм вычисляется по формуле:  . Ответ введите с точностью до 2-го знака после запятой.
. Ответ введите с точностью до 2-го знака после запятой.
Известна вероятность банкротства 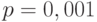 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до одного знака после запятой.)
лет. (Ответ округлить до одного знака после запятой.) 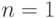 .
.
Даны пары значений  и
и  .
.
 | 8 | 22 | 17 | 34 | 27 | 57 | 14 | 20 | 40 |
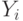 | 14 | 18 | 26 | 11 | 35 | 34 | 20 | 34 | 25 |
Если все значения  увеличить в 2 раза то коэффициент
увеличить в 2 раза то коэффициент  в уравнении регрессии
в уравнении регрессии  …
…
Доходности ценных бумаг входящих в состав портфеля ( ), их доли в портфеле (
), их доли в портфеле ( ) и дисперсии доходности (
) и дисперсии доходности (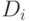 ) заданы в таблице. Ковариация доходностей равна 3.
) заданы в таблице. Ковариация доходностей равна 3.
 |  | 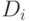 |
|---|---|---|
| 0,3 | 5 | 2 |
| 0,7 | 7 | 5 |
Найти среднее квадратичное отклонение доходности портфеля. Ответ введите с точностью до 2-го знака после запятой.
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить доходность инвестиций в проект с точностью до 1%. Ответ округлить до целых.
| Год | Поток |
|---|---|
| 0 | -200 |
| 1 | 50 |
| 2 | 100 |
| 3 | 120 |
| 4 | 150 |
| 5 | -50 |
| 6 | 200 |
| 7 | 300 |
Даны пары значений  и
и  .
.
 | 10 | 29 | 13 | 30 | 24 | 59 | 12 | 34 | 30 |
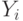 | 13 | 17 | 20 | 15 | 25 | 41 | 12 | 29 | 25 |
Найти коэффициент корреляции величин  и
и  .
.
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 10%. В ответе указать долю в портфеле бумаги номер 1. Ответ округлить до тысячных (три знака после запятой).
В таблице представлены доходности двух ценных бумаг в три периода времени. Вычислите коэффициент линейной корреляции между ними. Ответ округлите до двух знаков после запятой.
 | 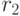 | 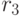 | |
|---|---|---|---|
| A | 4 | -1 | 2 |
| B | 10 | 11 | 6 |
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 10%. В ответе указать долю в портфеле бумаги номер 3. Ответ округлить до тысячных (три знака после запятой).
Номинал облигации 100 у.е., ежегодные выплаты составляют 4 у.е., учетная ставка ( ) меняется каждый год, как указано в таблице. Срок обращения облигации 5 лет. Определите дюрацию облигации. Ответ округлить до сотых.
) меняется каждый год, как указано в таблице. Срок обращения облигации 5 лет. Определите дюрацию облигации. Ответ округлить до сотых.
| Год |  (%) (%) |
|---|---|
| 1 | 4 |
| 2 | 7 |
| 3 | 6 |
| 4 | 9 |
| 5 | 8 |
Известна вероятность банкротства 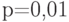 в течение года. Оцените количество лет за которые по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма менее одного.
в течение года. Оцените количество лет за которые по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма менее одного.
Номинал облигации 100 у.е., ежегодные выплаты составляют 9 у.е., учетная ставка ( ) меняется каждый год, как указано в таблице. Срок обращения облигации 8 лет. Определите рыночную цену облигации. Ответ округлить до сотых.
) меняется каждый год, как указано в таблице. Срок обращения облигации 8 лет. Определите рыночную цену облигации. Ответ округлить до сотых.
| Год |  (%) (%) |
|---|---|
| 1 | 7 |
| 2 | 8 |
| 3 | 2 |
| 4 | 4 |
| 5 | 3 |
| 6 | 4 |
| 7 | 8 |
| 8 | 8 |
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | R_1 | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 8 | 4 | 15 |
| 2 | 3 | 6 | 9 | 6 | 17 |
| 3 | 4 | 7 | 11 | 8 | 16 |
| 4 | 5 | 8 | 9 | 4 | 18 |
| 5 | 4 | 9 | 12 | 6 | 12 |
| 6 | 3 | 7 | 10 | 5 | 9 |
| 7 | 4 | 8 | 9 | 7 | 8 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 1. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 1. (Ответ округлить до сотых.)
Доходности ценных бумаг входящих в состав портфеля ( ), их доли в портфеле (
), их доли в портфеле ( ) и дисперсии доходности (
) и дисперсии доходности (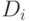 ) заданы в таблице. Ковариация доходностей равна 3.
) заданы в таблице. Ковариация доходностей равна 3.
 |  | 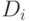 |
|---|---|---|
| 0,3 | 5 | 2 |
| 0,7 | 7 | 5 |
Найти доходность портфеля. Ответ введите с точностью до 2-го знака после запятой.
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 15%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -300 |
| 1 | 150 |
| 2 | 100 |
| 3 | 180 |
| 4 | -150 |
| 5 | -50 |
| 6 | 300 |
| 7 | 200 |
По оценкам экспертов ожидаемая доходность инвестиции может принять одно из значений  с вероятностями
с вероятностями  .
.
 |  |
| 8 | 0.1 |
| 10 | 0,05 |
| 12 | 0,1 |
| 14 | 0,2 |
| 16 | 0,3 |
| 18 | 0,1 |
| 20 | 0,1 |
| 22 | 0,05 |
Какова дисперсия доходности? (Дисперсия вычисляется по формуле: ![D=\sum[P_i(M-R_i)^2]](https://intuit.ru//sites/default/files/tex_cache/dd01ba4e12c7847589985fa7dbafd7b2.png) . Ответ округлить до десятых.)
. Ответ округлить до десятых.)
Номинал облигации 100 у.е., ежегодные выплаты составляют 4 у.е., учетная ставка 6%, срок обращения облигации 5 лет. Определите рыночную цену облигации. Ответ округлить до сотых.
В таблице представлены доходности двух ценных бумаг в три периода времени. Вычислите ковариацию между ними. Ответ округлите до двух знаков после запятой.
 | 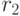 | 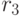 | |
|---|---|---|---|
| A | 4 | -1 | 2 |
| B | -2 | 5 | 10 |
Учетная ставка 5%. Ценная бумага куплена за 20 у.е., дивиденды за год составили 2 у.е.. Акция была продана за 40 у.е. через год. Каков доход (у.е.) от инвестирования в эту бумагу?
Экспертов привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Найдите вес 3-го эксперта. Ответ введите с точностью до 2-го знака после запятой.
| Оценка эксперта 1 | 5 | 7 | 9 | 7 |
| Оценка эксперта 2 | 4 | 3 | 2 | 5 |
| Оценка эксперта 3 | 3 | 1 | 5 | 9 |
| Оценка эксперта 4 | 5 | 7 | 5 | 8 |
| Оценка эксперта 5 | 3 | 4 | 4 | 8 |
| Реальное значение | 4 | 2 | 4 | 8 |
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 5%. В ответе указать максимальную доходность портфеля (по правилу 3-х сигм). Ответ округлить до десятых.
Известна вероятность банкротства 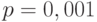 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.) 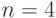 .
.
Известна вероятность банкротства 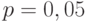 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.) 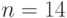 .
.
Какую сумму ежемесячно будет приносить вклад 300 000 рублей при учетной ставке 17% в год? Ответ округлите до целого числа.
Средства были инвестированы на 9 лет. Доходность от инвестирования (%) за каждый год приведена в таблице.
 | 6 |
 | 2 |
 | 7 |
 | 3 |
 | 5 |
 | 6 |
 | 1 |
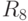 | 6 |
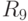 | 5 |
Какова средняя доходность за первые 2 года?
По оценкам экспертов ожидаемая доходность инвестиции может принять одно из значений  с вероятностями
с вероятностями  .
.
 |  |
| 8 | 0,1 |
| 10 | 0,05 |
| 12 | 0,1 |
| 14 | 0,2 |
| 16 | 0,3 |
| 18 | 0,1 |
| 20 | 0,1 |
| 22 | 0,05 |
Каково среднее квадратичное отклонение доходности? Среднее квадратичное отклонение (сигма - 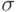 ) вычисляется по формуле:
) вычисляется по формуле: 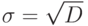 . Ответ округлить до сотых.
. Ответ округлить до сотых.
Деньги были вложены в три ценные бумаги в соответствии с таблицей, где D-дисперсия инструмента, r-доходность (в процентах). Рассчитайте дисперсию инвестиционного портфеля. Ответ округлите до сотых.
| 1 | 2 | 3 | |
|---|---|---|---|
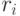 | 4 | 2 | 7 |
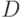 | 4 | 1 | 4 |
 | 0,2 | 0,2 | 0,6 |
В таблице представлены доходности двух ценных бумаг в три периода времени. Вычислите дисперсию бумаги B. Ответ округлите до двух знаков после запятой.
 | 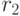 | 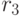 | |
|---|---|---|---|
| A | 4 | -1 | 2 |
| B | 10 | 11 | 6 |
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 10%. В ответе указать долю в портфеле бумаги номер 2. Ответ округлить до тысячных (три знака после запятой).
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 10%. В ответе указать дисперсию портфеля. Ответ округлить до тысячных (три знака после запятой).
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать среднее квадратичное отклонение доходности портфеля. Ответ округлить до тысячных (три знака после запятой).
Имеются 2 ценные бумаги с доходностями  =20 и
=20 и 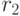 =10. Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать долю в портфеле бумаги номер 1. Ответ введите с точностью до 1-го знака после запятой.
=10. Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать долю в портфеле бумаги номер 1. Ответ введите с точностью до 1-го знака после запятой.
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | 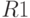 | 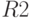 |  | 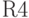 |  |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 9 | 8 | 6 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 1. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 1. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь
| Период |  |  |  |  |  |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 9 | 8 | 6 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 2. (Ответ введите с точностью до 1-го знака после запятой.)
. В ответе указать долю ценной бумаги № 2. (Ответ введите с точностью до 1-го знака после запятой.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  |  |  |  |  |
|---|---|---|---|---|---|
| 1 | 7 | 7 | 7 | 7 | 7 |
| 7 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 3. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 3. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  |  |  |  |  |
|---|---|---|---|---|---|
| 1 | 7 | 7 | 7 | 7 | 7 |
| 7 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 5. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 5. (Ответ округлить до сотых.)
Номинал облигации 100 у.е., ежегодные выплаты составляют 9 у.е., учетная ставка ( ) меняется каждый год, как указано в таблице. Срок обращения облигации 5 лет. Определите рыночную цену облигации. Ответ округлить до сотых.
) меняется каждый год, как указано в таблице. Срок обращения облигации 5 лет. Определите рыночную цену облигации. Ответ округлить до сотых.
| Год |  (%) (%) |
|---|---|
| 1 | 4 |
| 2 | 5 |
| 3 | 10 |
| 4 | 8 |
| 5 | 4 |
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 10%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -300 |
| 1 | 150 |
| 2 | 100 |
| 3 | 180 |
| 4 | -150 |
| 5 | -50 |
| 6 | 300 |
| 7 | 200 |
Известна вероятность банкротства 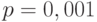 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.)  .
.
Известна вероятность банкротства 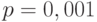 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.)  .
.
Известна вероятность банкротства 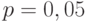 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.) 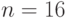 .
.
Эксперта привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Оцените среднюю ошибку эксперта. Ответ введите с точностью до 1-го знака после запятой.
| Оценка эксперта | 5 | 7 | 9 | 7 |
| Реальное значение | 4 | 2 | 4 | 8 |
Экспертов привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Оцените, какой из экспертов ошибался в своих оценках больше всех. В ответе укажите номер эксперта.
| Оценка эксперта 1 | 5 | 7 | 9 | 7 |
| Оценка эксперта 2 | 4 | 3 | 2 | 5 |
| Оценка эксперта 3 | 3 | 1 | 5 | 9 |
| Оценка эксперта 4 | 5 | 7 | 5 | 8 |
| Оценка эксперта 5 | 3 | 4 | 4 | 8 |
| Реальное значение | 4 | 2 | 4 | 8 |
Средства были инвестированы на 9 лет. Доходность от инвестирования (%) за каждый год приведена в таблице.
 | 5 |
 | 6 |
 | 3 |
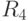 | 4 |
 | 6 |
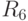 | 7 |
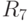 | 6 |
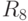 | 3 |
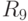 | 7 |
Какова средняя доходность за первые 2 года? (Ответ округлить до десятых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 8 | 4 | 15 |
| 2 | 3 | 6 | 9 | 6 | 17 |
| 3 | 4 | 7 | 11 | 8 | 16 |
| 4 | 5 | 8 | 9 | 4 | 18 |
| 5 | 4 | 9 | 12 | 6 | 12 |
| 6 | 3 | 7 | 10 | 5 | 9 |
| 7 | 4 | 8 | 9 | 7 | 8 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 4. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 4. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | 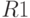 | 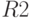 |  |  |  |
|---|---|---|---|---|---|
| 1 | 7 | 7 | 7 | 7 | 7 |
| 7 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 4. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 4. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | R_1 | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 8 | 4 | 15 |
| 2 | 3 | 6 | 9 | 6 | 17 |
| 3 | 4 | 7 | 11 | 8 | 16 |
| 4 | 5 | 8 | 9 | 4 | 18 |
| 5 | 4 | 9 | 12 | 6 | 12 |
| 6 | 3 | 7 | 10 | 5 | 9 |
| 7 | 4 | 8 | 9 | 7 | 8 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 2. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 2. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 8 | 4 | 15 |
| 2 | 3 | 6 | 9 | 6 | 17 |
| 3 | 4 | 7 | 11 | 8 | 16 |
| 4 | 5 | 8 | 9 | 4 | 18 |
| 5 | 4 | 9 | 12 | 6 | 12 |
| 6 | 3 | 7 | 10 | 5 | 9 |
| 7 | 4 | 8 | 9 | 7 | 8 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать минимально возможное среднее квадратичное отклонение доходности портфеля. (Ответ округлить до сотых.)
. В ответе указать минимально возможное среднее квадратичное отклонение доходности портфеля. (Ответ округлить до сотых.)
Ценная бумага куплена за 30 у.е., дивиденды за год составили 4 у.е.. Акция была продана за 60 у.е. Какова доходность (%) инвестирования в эту бумагу?
Чему будет равен дисконт(в %) на 1 год при учетной ставке 10%? Ответ округлите до 1 знака после запятой.
Чему будет равна стоимость актива, приносящего бесконечный ежегодный доход 20 000 при учетной ставке 10%?
По оценкам экспертов ожидаемая доходность инвестиции может принять одно из значений  с вероятностями
с вероятностями  .
.
 |  |
| 8 | 0,05 |
| 10 | 0,1 |
| 12 | 0,1 |
| 14 | 0,15 |
| 16 | 0,25 |
| 18 | 0,15 |
| 20 | 0,1 |
| 22 | 0,1 |
Какова средняя доходность? (Средняя доходность вычисляется по формуле: ![r=\sum[r_i*P_i]](https://intuit.ru//sites/default/files/tex_cache/0e7fe0e9bd6c6c7a5e5883602eefcb12.png) . Ответ округлить до десятых.)
. Ответ округлить до десятых.)
В таблице представлены доходности двух ценных бумаг в три периода времени. Вычислите коэффициент линейной корреляции между ними. Ответ округлите до двух знаков после запятой.
 | 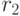 | 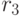 | |
|---|---|---|---|
| A | 1 | 2 | 4 |
| B | 2 | 4 | 3 |
Доходности ценных бумаг входящих в состав портфеля ( ), их доли в портфеле (
), их доли в портфеле ( ) и дисперсии доходности (
) и дисперсии доходности (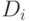 ) заданы в таблице. Ковариация доходностей равна 3.
) заданы в таблице. Ковариация доходностей равна 3.
 |  | 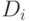 |
|---|---|---|
| 0,3 | 5 | 7 |
| 0,7 | 7 | 5 |
Найти дисперсию доходности портфеля. Ответ введите с точностью до 2-го знака после запятой.
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 7 | 7 | 7 | 7 | 7 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 1. ( Ответ введите с точностью до 1-го знака после запятой.)
. В ответе указать долю ценной бумаги № 1. ( Ответ введите с точностью до 1-го знака после запятой.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 7 | 7 | 7 | 7 | 7 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать долю ценной бумаги № 2. (Ответ округлить до сотых.)
. В ответе указать долю ценной бумаги № 2. (Ответ округлить до сотых.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период |  | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 12 | 6 | 9 | 8 | 6 |
| 2 | 13 | 7 | 8 | 4 | 6 |
| 3 | 11 | 6 | 10 | 9 | 5 |
| 4 | 9 | 8 | 11 | 4 | 5 |
| 5 | 7 | 7 | 9 | 10 | 9 |
| 6 | 10 | 5 | 8 | 5 | 4 |
| 7 | 12 | 6 | 9 | 8 | 5 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность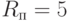 . В ответе указать долю ценной бумаги № 3. (Ответ введите с точностью до 1-го знака после запятой.)
. В ответе указать долю ценной бумаги № 3. (Ответ введите с точностью до 1-го знака после запятой.)
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | R_1 | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 8 | 4 | 15 |
| 2 | 3 | 6 | 9 | 6 | 17 |
| 3 | 4 | 7 | 11 | 8 | 16 |
| 4 | 5 | 8 | 9 | 4 | 18 |
| 5 | 4 | 9 | 12 | 6 | 12 |
| 6 | 3 | 7 | 10 | 5 | 9 |
| 7 | 4 | 8 | 9 | 7 | 8 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать минимально возможную дисперсию портфеля. (Ответ введите с точностью до 3-го знака после запятой.)
. В ответе указать минимально возможную дисперсию портфеля. (Ответ введите с точностью до 3-го знака после запятой.)
Номинал облигации 100 у.е., ежегодные выплаты составляют 9 у.е., учетная ставка 7%, срок обращения облигации 8 лет. Определите дюрацию облигации. Ответ округлить до сотых.
Номинал облигации 100 у.е., ежегодные выплаты составляют 8 у.е., учетная ставка ( ) меняется каждый год, как указано в таблице. Срок обращения облигации 5 лет. Определите рыночную цену облигации. Ответ округлить до сотых.
) меняется каждый год, как указано в таблице. Срок обращения облигации 5 лет. Определите рыночную цену облигации. Ответ округлить до сотых.
| Год |  (%) (%) |
|---|---|
| 1 | 5 |
| 2 | 4 |
| 3 | 6 |
| 4 | 7 |
| 5 | 8 |
Известна вероятность банкротства 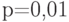 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.) 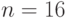 .
.
Экспертов привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Найдите вес 2-го эксперта. Ответ введите с точностью до 1-го знака после запятой.
| Оценка эксперта 1 | 5 | 7 | 9 | 7 |
| Оценка эксперта 2 | 4 | 3 | 2 | 5 |
| Оценка эксперта 3 | 3 | 1 | 5 | 9 |
| Оценка эксперта 4 | 5 | 7 | 5 | 8 |
| Оценка эксперта 5 | 3 | 4 | 4 | 8 |
| Реальное значение | 4 | 2 | 4 | 8 |
Экспертов привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Найдите сумму весов экспертов. Ответ округлите до сотых.
| Оценка эксперта 1 | 3 | 5 | 4 | 5 |
| Оценка эксперта 2 | 5 | 3 | 3 | 5 |
| Оценка эксперта 3 | 4 | 3 | 5 | 9 |
| Оценка эксперта 4 | 5 | 6 | 5 | 8 |
| Оценка эксперта 5 | 3 | 4 | 4 | 8 |
| Реальное значение | 6 | 4 | 5 | 8 |
По оценкам экспертов ожидаемая доходность инвестиции может принять одно из значений  с вероятностями
с вероятностями  .
.
 |  |
| 8 | 0,1 |
| 10 | 0,05 |
| 12 | 0,1 |
| 14 | 0,2 |
| 16 | 0,3 |
| 18 | 0,1 |
| 20 | 0,1 |
| 22 | 0,05 |
Какова средняя доходность? (Средняя доходность вычисляется по формуле: ![r=\sum[r_i*P_i]](https://intuit.ru//sites/default/files/tex_cache/0e7fe0e9bd6c6c7a5e5883602eefcb12.png) .)
.)
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 5%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -300 |
| 1 | 150 |
| 2 | 100 |
| 3 | 180 |
| 4 | -150 |
| 5 | -50 |
| 6 | 300 |
| 7 | 200 |
Чему будет равен дисконт (в %) на 1 год при учетной ставке 5%? Ответ округлите до 1 знака после запятой.
Экспертов привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Оцените, какой из экспертов ошибался в своих оценках меньше всех. В ответе укажите номер эксперта.
| Оценка эксперта 1 | 3 | 5 | 4 | 5 |
| Оценка эксперта 2 | 5 | 3 | 3 | 5 |
| Оценка эксперта 3 | 4 | 3 | 5 | 9 |
| Оценка эксперта 4 | 5 | 6 | 5 | 8 |
| Оценка эксперта 5 | 7 | 3 | 7 | 6 |
| Реальное значение | 6 | 4 | 5 | 8 |
Экспертов привлекали 5 раз для прогноза доходности инвестиционного проекта. Реальная доходность проекта в 4-х случаях уже известна. Оцените возможное реальное значение в пятом случае, если известны оценки экспертов. Ответ округлите до сотых.
| Оценка эксперта 1 | 3 | 5 | 4 | 5 | 4 |
| Оценка эксперта 2 | 5 | 3 | 3 | 5 | 5 |
| Оценка эксперта 3 | 4 | 3 | 5 | 9 | 6 |
| Оценка эксперта 4 | 5 | 6 | 5 | 8 | 5 |
| Оценка эксперта 5 | 7 | 3 | 7 | 6 | 4 |
| Реальное значение | 6 | 4 | 5 | 8 | ? |
Учетная ставка 5%. Куплены три ценные бумаги по ценам (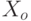 ), которые принесли дивиденды (
), которые принесли дивиденды ( ).
).
 | 20 | 15 | 30 |
 | 2 | 3 | 5 |
Каковы суммарные дивиденды?
Учетная ставка 7%, на депозит положено 1 000 000 рублей. Какая сумма будет на депозите через 3 года? Ответ округлите до целого числа.
Доходности ценных бумаг входящих в состав портфеля ( ), их доли в портфеле (
), их доли в портфеле ( ) и дисперсии доходности (
) и дисперсии доходности (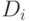 ) заданы в таблице. Ковариация доходностей равна 3.
) заданы в таблице. Ковариация доходностей равна 3.
 |  | 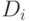 |
|---|---|---|
| 0,2 | 7 | 3 |
| 0,8 | 10 | 8 |
Найти дисперсию доходности портфеля. Ответ введите с точностью до 2-го знака после запятой.
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 5%. В ответе указать долю в портфеле бумаги номер 1. Ответ округлить до одного знака после запятой.
Даны пары значений 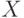 и
и  .
.
 | 12 | 24 | 16 | 27 | 28 | 67 | 18 | 26 | 38 |
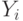 | 15 | 19 | 23 | 12 | 30 | 43 | 10 | 33 | 28 |
Найти остаточное среднее квадратичное отклонение.
Номинал облигации 100 у.е., ежегодные выплаты составляют 4 у.е., учетная ставка 6%, срок обращения облигации 5 лет. Определите дюрацию облигации. Ответ округлить до сотых.
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 10%. Ответ округлить до ближайшего целого.
| Год | Поток |
|---|---|
| 0 | -200 |
| 1 | 50 |
| 2 | 100 |
| 3 | 120 |
| 4 | 150 |
| 5 | -50 |
| 6 | 200 |
| 7 | 300 |
Известны денежные потоки инвестиционного проекта (отрицательные величины - затраты, положительные - поступления). Определить стоимость проекта если учетная ставка равна 35%. Ответ округлить до одного знака после запятой.
| Год | Поток |
|---|---|
| 0 | -500 |
| 1 | 150 |
| 2 | 200 |
| 3 | 250 |
| 4 | 300 |
| 5 | -200 |
| 6 | 150 |
| 7 | 300 |
Деньги были вложены в три ценные бумаги в соответствии с таблицей, где D-дисперсия инструмента, r-доходность (в процентах). Рассчитайте дисперсию инвестиционного портфеля. Ответ округлите до сотых.
| 1 | 2 | 3 | |
|---|---|---|---|
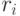 | 5 | 3 | 4 |
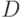 | 1 | 4 | 9 |
 | 0,2 | 0,4 | 0,4 |
Доходности ценных бумаг входящих в состав портфеля ( ), их доли в портфеле (
), их доли в портфеле ( ) и дисперсии доходности (
) и дисперсии доходности (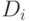 ) заданы в таблице. Ковариация доходностей равна 3.
) заданы в таблице. Ковариация доходностей равна 3.
 |  | 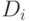 |
|---|---|---|
| 0,6 | 6 | 5 |
| 0,4 | 8 | 10 |
Найти доходность портфеля. Ответ введите с точностью до 1-го знака после запятой.
Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | R_1 | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 8 | 4 | 15 |
| 2 | 3 | 6 | 9 | 6 | 17 |
| 3 | 4 | 7 | 11 | 8 | 16 |
| 4 | 5 | 8 | 9 | 4 | 18 |
| 5 | 4 | 9 | 12 | 6 | 12 |
| 6 | 3 | 7 | 10 | 5 | 9 |
| 7 | 4 | 8 | 9 | 7 | 8 |
Найти по методу Шарпа оптимальный состав портфеля, обеспечивающий доходность  . В ответе указать минимальную оценку доходности портфеля по правилу трех сигм. (Ответ округлить до сотых.)
. В ответе указать минимальную оценку доходности портфеля по правилу трех сигм. (Ответ округлить до сотых.)
Известна вероятность банкротства 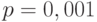 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.)  .
.
В таблице представлены доходности двух ценных бумаг в три периода времени. Вычислите среднюю доходность бумаги B.
 | 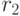 | 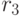 | |
|---|---|---|---|
| A | 4 | -1 | 2 |
| B | 10 | 11 | 6 |
В таблице представлены доходности двух ценных бумаг в три периода времени. Вычислите ковариацию между ними. Ответ округлите до двух знаков после запятой.
 | 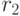 | 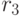 | |
|---|---|---|---|
| A | 4 | -1 | 2 |
| B | 10 | 11 | 6 |
Имеются данные о доходности трех ценных бумаг за пять периодов.
 |  |  |
|---|---|---|
| 2 | 5 | 9 |
| 3 | 7 | 7 |
| 2 | 4 | 10 |
| 4 | 8 | 5 |
| 3 | 7 | 8 |
Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать минимальную доходность портфеля (по правилу 3-х сигм). Ответ округлить до сотых (два знака после запятой).
Известна вероятность банкротства 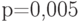 в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за
в течение года. Оцените по правилу трех сигм максимальное количество банкротств, с которыми может столкнуться фирма за  лет. (Ответ округлить до сотых.)
лет. (Ответ округлить до сотых.) 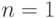 .
.
Экспертов привлекали 4 раза для прогноза доходности инвестиционного проекта. Реальная доходность проекта уже известна. Найдите сумму весов экспертов. Ответ введите с точностью до 1-го знака после запятой.
| Оценка эксперта 1 | 5 | 7 | 9 | 7 |
| Оценка эксперта 2 | 4 | 3 | 2 | 5 |
| Оценка эксперта 3 | 3 | 1 | 5 | 9 |
| Оценка эксперта 4 | 5 | 7 | 5 | 8 |
| Оценка эксперта 5 | 3 | 4 | 4 | 8 |
| Реальное значение | 4 | 2 | 4 | 8 |
Доходности ценных бумаг входящих в состав портфеля ( ), их доли в портфеле (
), их доли в портфеле ( ) и дисперсии доходности (
) и дисперсии доходности (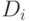 ) заданы в таблице. Ковариация доходностей равна 3.
) заданы в таблице. Ковариация доходностей равна 3.
 |  | 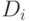 |
|---|---|---|
| 0,2 | 7 | 3 |
| 0,8 | 10 | 8 |
Найти среднее квадратичное отклонение доходности портфеля. Ответ введите с точностью до 2-го знака после запятой.
