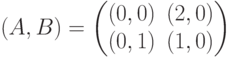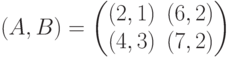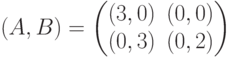Игра, задаваемая биматрицей 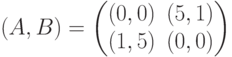 разыгрывается повторно, если игроки выбрали стратегии с несовпадающими номерами. Выигрыши игроков в повторениях суммируются, причем каждому из них известен выигрыш, полученный на первом этапе. Какой вид имеет биматрица игры, соответствующая повторно разыгрываемой исходной игре?
разыгрывается повторно, если игроки выбрали стратегии с несовпадающими номерами. Выигрыши игроков в повторениях суммируются, причем каждому из них известен выигрыш, полученный на первом этапе. Какой вид имеет биматрица игры, соответствующая повторно разыгрываемой исходной игре?
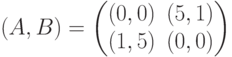
(Отметьте один правильный вариант ответа.)
Варианты ответа
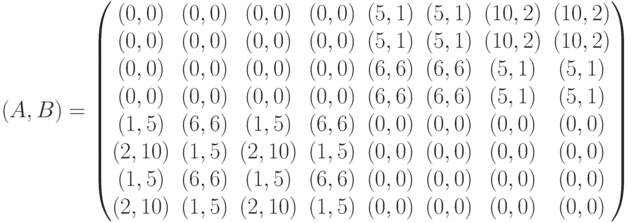
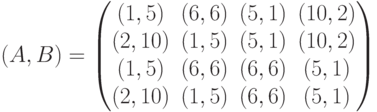
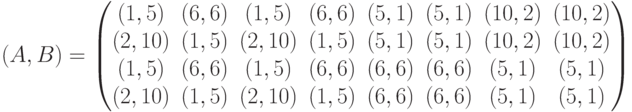

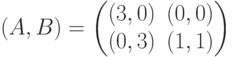
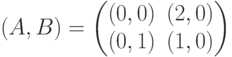
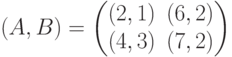
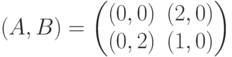
 где (m,n) – начальные запасы ресурсов первого и второго игрока соответственно. Какой вид имеет матрица антагонистической игры, соответствующая игре в позиционной форме, при начальных запасах ресурсов (1,2)?
где (m,n) – начальные запасы ресурсов первого и второго игрока соответственно. Какой вид имеет матрица антагонистической игры, соответствующая игре в позиционной форме, при начальных запасах ресурсов (1,2)?