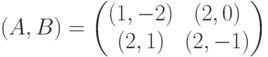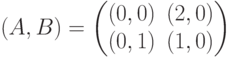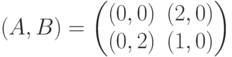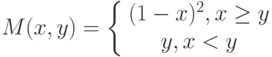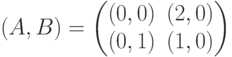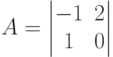Два предприятия, обладающие производственными возможностями Ki, i=1,2, продают на рынке один и тот же вид продукции. Возможности рынка ограничены суммой денег С. Пусть xi, 0≤xi≤Ki - количество продукции, производимой предприятием i, а - себестоимость единицы продукции, pi, a≤pi≤C/xi - цена единицы продукции. Предположим, что: предприятия не знают объемов выпуска и выбираемых цен продукции друг друга; на рынке вначале покупается более дешевая продукция; в случае равенства цен покупается продукция второго предприятия. Укажите вид критерия эффективности первого предприятия, если его цель состоит в разорении партнера
Какое из утверждений справедливо для биматричной игры
Дуэль истребитель-бомбардировщик. Пусть в дуэли истребитель-бомбардировщик самолеты летят навстречу друг другу с единичного рас-стояния, и цель второй стороны (бомбардировщика) состоит в выживании. Дуэль заканчивается, если одна из сторон поразила противника или стороны исчерпали боеприпасы. Вероятности попадания описываются в виде функцийирасстояния между самолетами. Полезность исходов дуэли для второй стороны описывается таблицей
| бомбардировщик сбит | бомбардировщик уцелел |
| истребитель сбит | 0 | 1 |
| истребитель уцелел | 0 | 1 |
Каков вид усредненной полезности бомбардировщика, если каждая из сторон может произвести один выстрел и дуэлянты не слышат выстрелов друг друга - дуэль бесшумная
Говорят, что стратегия x1′ строго доминирует стратегию x"1 в игре <X1,X2,M1(x1,x2),M2(x1,x2)>, если (∀x2∈X2)M1(x1′,x2) >M1(x1",x2). Какие утверждения справедливы для игры, в которой множества стратегий игроков Х1={1,2,3,4}, Х2={1,2,3,4,5}, а функции выигрыша заданы в виде
Пусть в игре двух лиц множества стратегий конечны X1=X2={1,2} и порядок ходов заранее не определен. Игроку, делающему ход вторым, известен выбор партнера. В какой из игр не возникает борьба за очередность ходов?
Позиционная игра. Антагонистическая игра с полной информацией, в которой первым ходит первый игрок, задана деревом  Каковы размеры матрицы игры?
Каковы размеры матрицы игры?
Две конкурирующие фирмы производят сезонный товар, пользующийся спросом в период времени 0≤t≤1. Качество конкурирующих товаров зависит от времени их поступления на рынок - чем позже товар появляется на рынке, тем качество его выше. Примем, что покупатели при отсутствии конкуренции приобретают товар, имеющийся на рынке, а при наличии двух товаров отдают предпочтение товару более высокого качества. Если товары поступают на рынок одновременно, то они пользуются одинаковым спросом. Продажа товара приносит производителю доход С в единицу времени. Каким выражением описывается критерий эффективности первой стороны, если ее цель состоит в максимизации дохода?
Задача линейного программирования с ограничениями типа неравенств имеет вид w1*+w2*+w3*=max{w1+w2+w3:wj≥0,1≤j≤3,w1+3w2+5w3≤1,4w1+2w2+w3≤1} Для какой матричной игры решение задачи линейного программирования определяет оптимальную стратегию второго игрока?
Установить, какие точки являются седловыми для функции в области 0≤x≤1,0≤y≤1
Чему равны гарантированные выигрыши сторон? Какая сделка (u0,v0) удовлетворяет аксиомам Нэша?
Являются ли ситуациями равновесия в биматричной игре чистые стратегии
Какое из утверждений справедливо для игры <X1,X2,M1(x1,x2), M2(x1,x2)>, где Х1=Х2=[-1,1], M1(x1,x2)= M2(x1,x2)=x1x2?
Контроль качества продукции. Заказчик, осуществляя приемку у исполнителя сложного технического изделия, может выбрать одно из двух решений: признать изделие годным и принять его в эксплуатацию (покрывая стоимость обнаруженных впоследствии дефектов) либо признать изделие непригодным для эксплуатации и потребовать замены отдельных (возможно, некачественных) узлов. Качество изделия может быть удовлетворительным или неудовлетворительным, в зависимости от соблюдения технологии изготовления изделия. Замена исправных узлов оплачивается заказчиком и составляет условную единицу. Стоимость обнаруженных во время эксплуатации дефектов обходится заказчику в два раза дороже, в остальных случаях потери отсутствуют. Матрица потерь заказчика имеет вид  Пусть заказчик перед принятием решения о приемке изделия проводит тестирование изделия. Результаты тестирования зависят от качества изделия и описываются условными распределениями вероятностей
Пусть заказчик перед принятием решения о приемке изделия проводит тестирование изделия. Результаты тестирования зависят от качества изделия и описываются условными распределениями вероятностей
| z1- тестирование прошло успешно | z2 - выполнилась большая часть тестов | z3- выполнилась меньшая часть тестов | z4 - ни один из тестов не выполнился |
| p(z/1) | 0,6 | 0,3 | 0,1 | 0 |
| p(z/2) | 0 | 0,1 | 0,5 | 0,4 |
Чему равен риск
ρ(ξ,d) от применения решающей функции
при равновозможных состояниях природы?
Какой вид имеет паретовская граница множества S? 
В статистической 2x3 игре
| z1 | z2 |
| p(z/1) | 0,25 | 0,75 |
| p(z/2) | 0,75 | 0,25 |
Какое решение принять статистику, если
ξ=(0.9,0.1) и в результате эксперимента наблюдается
z2?
Каждая из противоборствующих сторон пытается овладеть позицией противника. Первая сторона располагает двумя подразделениями, вторая – одним подразделением. Силы сторон распределяются для обороны собственной позиции и атаки позиции противника. Позиция считается занятой той стороной, которая выделила для ее захвата большее (целое) число подразделений. Если атакующие силы недостаточны для захвата позиций, то они отступают, и игра начинается заново. Игра завершается, если захвачена одна из позиций. Примем, что интересы сторон противоположны. При этом первая сторона выигрывает единицу, если ей удалось завладеть позицией противника, не потеряв своей, и проигрывает единицу, потеряв свой лагерь. Если в течение T периодов столкновений ни одна из позиций не захвачена, то игра завершается вничью. Для случая Т=2 дерево игры имеет вид  где пара (i,j) означает "оставить i подразделений для обороны и направить j подразделений для атаки". Установите, какая 2x2 матрица описывает выигрыши первой стороны в первом из двух возможных периодов игры
где пара (i,j) означает "оставить i подразделений для обороны и направить j подразделений для атаки". Установите, какая 2x2 матрица описывает выигрыши первой стороны в первом из двух возможных периодов игры

Пусть в игре двух лиц <X1,X2,M1(x1,x2),M2(x1,x2)> множества стратегий конечны X1=X2={1,2}, а критерии заданы в виде 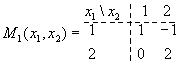
 Какое из утверждений справедливо, если игрокам известны критерии, множества стратегий и решения принимаются одновременно (случай симметричного распределения информации об игре)?
Какое из утверждений справедливо, если игрокам известны критерии, множества стратегий и решения принимаются одновременно (случай симметричного распределения информации об игре)?
Установить, какие точки являются седловыми для функции в области 0≤x≤1, 0≤y≤1
Обслуживание загородных маршрутов. Известно, что жители больших городов, придерживаясь рационального принципа проведения воскресного отдыха на свежем воздухе, все более охотно выезжают за город, используя автобусный транспорт. Поэтому в выходные дни возникает проблема выделения дополнительных автобусов, следующих в загородные места отдыха. Очевидно, что потребность в дополнительном транспорте зависит от погоды в выходной день. Функция потерь транспортного предприятия, вычисленная на основе прошлых лет, имеет вид  Графики функций математического ожидания потерь (функций риска) ρ=ρ(ξαi),1≤i≤3 в зависимости от априорного распределения вероятностей ζ=(ζ,1-ζ),0≤ζ≤1 на состояниях природы {плохая, хорошая}={1, 2} имеют вид
Графики функций математического ожидания потерь (функций риска) ρ=ρ(ξαi),1≤i≤3 в зависимости от априорного распределения вероятностей ζ=(ζ,1-ζ),0≤ζ≤1 на состояниях природы {плохая, хорошая}={1, 2} имеют вид  Пусть в задаче обслуживания загородных маршрутов диспетчер принимает решение с учетом показаний барометра, причем, в силу несовершенства прибора, показания {дождь, переменно, ясно, очень сухо}={z1,z2,z3,z4} связаны с состоянием погоды стохастически:
Пусть в задаче обслуживания загородных маршрутов диспетчер принимает решение с учетом показаний барометра, причем, в силу несовершенства прибора, показания {дождь, переменно, ясно, очень сухо}={z1,z2,z3,z4} связаны с состоянием погоды стохастически:
| z1 | z2 | z3 | z4 |
| p(z/1) | 0,6 | 0,3 | 0,1 | 0 |
| p(z/2) | 0,1 | 0,1 | 0,5 | 0,3 |
Сколько решающих функций (правил преобразования показаний барометра в решения) имеется у диспетчера?
Какой вид имеет паретовская граница множества S? 
Дуэль истребитель-бомбардировщик. Пусть в дуэли истребитель-бомбардировщик самолеты летят навстречу друг другу с единичного рас-стояния, и цель первой стороны (истребителя) состоит в поражении противника. Дуэль заканчивается, если одна из сторон поразила противника или стороны исчерпали боеприпасы. Вероятности попадания описываются в виде функций p1(x) и p2(y) расстояния между самолетами. Полезность исхо-дов дуэли для первой стороны описывается таблицей
| бомбардировщик сбит | бомбардировщик уцелел |
| истребитель сбит | 1 | 0 |
| истребитель уцелел | 1 | 0 |
Каков вид усредненной полезности истребителя, если каждая из сторон может произвести один выстрел и дуэлянты слышат выстрелы друг друга - дуэль шумная?
Выбор маршрута. Транспортное предприятие планирует открыть автобусную линию от нового микрорайона до центра города либо по маршруту α1, либо по более протяженному маршруту α2 . Известно, что 30% жителей микрорайона работает в организациях, расположенных в окрестности маршрута α1 (первое состояние), и 70% - в окрестности маршрута α2 (второе состояние). Потери транспортного предприятия оцениваются матрицей  Отношения правдоподобия p(z/2)/p(z/1) для результатов тестирования в задаче о выборе маршрута описываются таблицей
Отношения правдоподобия p(z/2)/p(z/1) для результатов тестирования в задаче о выборе маршрута описываются таблицей
| z1 - на работу и домой по маршруту α1 | z2 - на работу и домой по маршруту α2 | z3- на работу по маршруту α1, домой по маршруту α2 | z4 - на работу по маршруту α2, домой по маршруту α1 |
| p(z/2)/p(z/1) | 3/5 | 2 | 1 | 1 |
Каков вид байесовской решающей функции при априорном распределении вероятностей
ξ=(0.3,0.7)
Какие пары чистых стратегий игроков в биматричной игре являются устойчивыми и не являются эффективными?
Пусть в конечной игре двух лиц <X1,X2,M1(x1,x2),M2(x1,x2)> X1={1,2,3,4}, X2={1,2,3,4,5}
Какие стратегии игроков являются наилучшими по гарантированному результату?
Выбор структуры посевов. Руководство сельскохозяйственного предприятия решает проблему выбора участков земли для посадки картофеля. Для хорошего урожая требуется определенное количество влаги. В среднем максимальные урожаи получаются при решении о посадке картофеля на участке, характеризующемся большой влажностью почвы (решение α2) при засушливом лете (второе состояние природы), или при решении о посадке картофеля на сухом участке (решение α1) при дождливом лете (первое состояние природы). Потери сельскохозяйственного предприятия оцениваются матрицей  Пусть при решении проблемы выбора участков земли для посадки используется дополнительная информация о состоянии природы, полученная в результате наблюдений за погодой весной, в период посадки. Результаты наблюдений на основе многолетней статистики определяют условные распределения (в зависимости от состояния природы)
Пусть при решении проблемы выбора участков земли для посадки используется дополнительная информация о состоянии природы, полученная в результате наблюдений за погодой весной, в период посадки. Результаты наблюдений на основе многолетней статистики определяют условные распределения (в зависимости от состояния природы)
| z1 - большое количество осадков | z2 - малое количество осадков |
| p(z/1) | 0,6 | 0,4 |
| p(z/2) | 0,2 | 0,8 |
Чему равен риск
ρ(ξ,d) от применения решающей функции
при априорном распределении вероятностей
ξ(o.5,0.5)?
Выберите правильное утверждение: ситуацией равновесия по Нэшу в игре <X1,X2,M1(x1,x2), M2(x1,x2)> называется пара стратегий (x10,x20),удовлетворяющая соотношениям
Какие пары стратегий являются седловыми точками матричной игры
Обслуживание загородных маршрутов. Известно, что жители больших городов, придерживаясь рационального принципа проведения воскресного отдыха на свежем воздухе, все более охотно выезжают за город, используя автобусный транспорт. Поэтому в выходные дни возникает проблема выделения дополнительных автобусов, следующих в загородные места отдыха. Очевидно, что потребность в дополнительном транспорте зависит от погоды в выходной день. Функция потерь транспортного предприятия, вычисленная на основе прошлых лет, имеет вид  Графики функций математического ожидания потерь (функций риска) ρ=ρ(ξαi),1≤i≤3 в зависимости от априорного распределения вероятностей ζ=(ζ,1-ζ),0≤ζ≤1 на состояниях природы {плохая, хорошая}={1, 2} имеют вид
Графики функций математического ожидания потерь (функций риска) ρ=ρ(ξαi),1≤i≤3 в зависимости от априорного распределения вероятностей ζ=(ζ,1-ζ),0≤ζ≤1 на состояниях природы {плохая, хорошая}={1, 2} имеют вид  Пусть априорное распределение вероятностей на состояниях природы в задаче обслуживания загородных маршрутов есть ξ=(1/2,1/2) (состояния природы равновозможны), и выбору решения предшествует эксперимент. Какая из решающих функций, d1 или d2, указанных в таблице, предпочтительнее?
Пусть априорное распределение вероятностей на состояниях природы в задаче обслуживания загородных маршрутов есть ξ=(1/2,1/2) (состояния природы равновозможны), и выбору решения предшествует эксперимент. Какая из решающих функций, d1 или d2, указанных в таблице, предпочтительнее?
| z1 | z2 | z3 | z4 |
| d1(z) | α3 | α2 | α1 | α1 |
| d1(z) | α3 | α2 | α2 | α1 |
Какие пары чистых стратегий игроков в биматричной игре являются устойчивыми и эффективными?
Пусть в задаче обслуживания загородных маршрутов диспетчер принимает решение с учетом показаний барометра, причем в силу несовершенства прибора показания {дождь, переменно, ясно, очень сухо}={z1,z2,z3,z4} связаны с состоянием погоды стохастически:
| z1 | z2 | z3 | z4 |
| p(z/1) | 0,6 | 0,3 | 0,1 | 0 |
| p(z/2) | 0,1 | 0,1 | 0,5 | 0,3 |
Пусть априорное распределение вероятностей на состояниях природы в задаче обслуживания загородных маршрутов есть
ξ=(0,1), и выбору решения предшествует эксперимент. Какая из решающих функций d
1 или d
2, указанных в таблице, предпочтительнее?
| z1 | z2 | z3 | z4 |
| d1(z) | α3 | α2 | α1 | α1 |
| d2(z) | α3 | α1 | α1 | α1 |
Две конкурирующие фирмы производят сезонный товар, пользующийся спросом в период времени 0≤t≤1. Качество конкурирующих товаров зависит от времени их поступления на рынок – чем позже товар появляется на рынке, тем качество его выше. Примем, что покупатели при отсутствии конкуренции приобретают товар, имеющийся на рынке, а при наличии двух товаров отдают предпочтение товару более высокого качества. Если товары поступают на рынок одновременно, то они пользуются одинаковым спросом. Продажа товара приносит производителю доход С в единицу времени. Каким выражением описывается критерий эффективности первой сто-роны, если ее цель состоит в получении дохода, превосходящего доход конкурента?
Две противоборствующие стороны пытаются овладеть двумя позициями. Для этого первая сторона располагает тремя подразделениями, вторая - четырьмя подразделениями (например, полками). Каждый из противников может выделить для захвата любой из позиций целое число подразделений (в том числе и нулевое), полностью расходуя ресурсы. Позиция считается занятой той стороной, которая выделила для ее захвата большее число подразделений. Какой вид имеет критерий эффективности первой стороны, если цели сторон состоят в захвате большего числа позиций, чем у противника?
Две противоборствующие стороны пытаются овладеть двумя позициями. Для этого первая сторона располагает тремя подразделениями, вторая - четырьмя подразделениями (например, полками). Каждый из противников может выделить для захвата любой из позиций целое число подразделений (в том числе и нулевое), полностью расходуя ресурсы. Позиция считается занятой той стороной, которая выделила для ее захвата большее число подразделений. Какой вид имеет критерий эффективности первой стороны, если ее цель состоит в уничтожении максимального числа подразделений противника? Предполагается, что одно подразделение первой стороны уничтожает одно подразделение второй при столкновении
Пусть в конечной игре двух лиц <X1,X2,M1(x1,x2),M2(x1,x2)> X1={1,2,3,4}, X2={1,2,3,4,5} Укажите стратегии второго игрока, являющиеся наилучшими по гарантированному результату
В игре двух лиц <X1,X2,M1(x1,x2),M2(x1,x2)>X1=[-1,1], X2=[0,2], M1(x1,x2)=M2(x1,x2)=-x1-x2. Какой выигрыш гарантирует первому игроку стратегия x1=1?
Дуополия с назначением выпусков. Два производителя одного и того же товара могут производить его в объемах 0≤xi≤0.5, i=1,2. Затраты на выпуск единицы продукции составляют ci(xi)=Cixi,Ci>0. Товар подается на рынке по цене p(x)=1-x, где x=x1+x2 - совокупное предложение товара. Прибыль i-го производителя от выпуска товара в объеме xi описывается функцией Mi(xix2)=xip(x)-ci(xi). Какие объемы выпуска являются оптимальными по Парето (эффективными) в дуополии с назначением выпусков при C1=0,5, C2=0,5?
Дуополия с назначением выпусков. Два производителя одного и того же товара могут производить его в объемах 0≤xi≤0.5, i=1,2. Затраты на выпуск единицы продукции составляют ci(xi)=Cixi,Ci>0. Товар подается на рынке по цене p(x)=1-x, где x=x1+x2 - совокупное предложение товара. Прибыль i-го производителя от выпуска товара в объеме xi описывается функцией Mi(xix2)=xip(x)-ci(xi). Какие объемы выпуска являются устойчивыми (образуют ситуацию равновесия по Нэшу) в дуополии с назначением выпусков при C1=0,4, C2=0,4
Какие объемы выпуска являются оптимальными по Парето (эффективными) в дуополии с назначением выпусков при C1=0,7, C2=0,7
Пусть в игре двух лиц <X1,X2,M1(x1,x2),M2(x1,x2)> множества стратегий конечны X1=X2={1,2} и порядок ходов заранее не определен. Игроку, делающему ход вторым, известен выбор партнера. В какой из игр возникает борьба за право первого хода?
Пусть в игре двух лиц <X1,X2,M1 (x1,x2),M2 (x1, x2)> множества стратегий конечны X1=X2={1,2}, а критерии заданы в виде 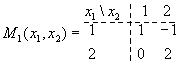
 Какое из утверждений справедливо, если игрокам известны критерии, множества стратегий и первым ходит первый игрок (случай несимметричного распределения информации об игре)?
Какое из утверждений справедливо, если игрокам известны критерии, множества стратегий и первым ходит первый игрок (случай несимметричного распределения информации об игре)?
Два производителя одного и того же товара могут производить его в объемах 0≤xi≤1,i=1,2. Затраты на выпуск единицы продукции составляют ci(xi)=Cixi,Ci>0 Товар подается на рынке по цене p(x)=1-x, где x=x1+x2 - совокупное предложение товара. Прибыль i-го производителя от выпуска товара в объеме xi описывается функцией M1(x1,x2)=xip (x)-ci(xi) Какое решение об объеме выпуска следует принять первому производителю, обладающим правом первого хода, если второй использует в качестве ответа функцию x2 =0,6-1,5x1 при C1=0,6 C2=0,4?
Рынок товара. Зависимость спроса на однородный товар от цены p за единицу товара имеет видПоступление товара на рынок описывается функцией предложения pmin=2, pmax=12. Пусть посредник при понижении цены осуществляет закупку двух единиц товара, которые сбывает при повышении цены. Чему равна прибыль посредника в результате операции купли-продажи, если в начальный момент времени p=8, S(8)=18?
Рынок товара. Зависимость спроса на однородный товар от цены p за единицу товара имеет вид Поступление товара на рынок описывается функцией предложенияpmin=2, pmax=12. При какой цене товара имеет баланс спроса и предложения?
Рынок товара. Зависимость спроса на однородный товар от цены p за единицу товара имеет вид Поступление товара на рынок описывается функцией предложения pmin=2, pmax=12. Пусть посредник при понижении цены осуществляет закупку двух единиц товара, которые сбывает при повышении цены. Чему равна прибыль посредника в результате операции купли-продажи, если в начальный момент времени p=8, S(8)=12
Чему равен минимальный гарантированный проигрыш второго игрока в антагонистической игре с ядром и множествами стратегий 0≤x≤1, 0≤y≤1?
Чему равен максимальный гарантированный выигрыш первого игрока в антагонистической игре с ядром M(x,y)=-(x-y)2 и множествами стратегий 0≤x≤1, 0≤y≤1?
Какому типу принадлежит игра <X,Y,M1(x, y),M2 (x, y)>, в которой X={x:0≤x≤1},Y={y:0≤y≤1}
Установить, какие точки являются седловыми для функции в области 0≤x≤1,0≤y≤1
Установить, какие точки являются седловыми для функции в области 0≤x≤1,0≤y≤1
Дуэль истребитель-бомбардировщик. Пусть в дуэли истребитель-бомбардировщик самолеты летят навстречу друг другу с единичного расстояния, и цель первой стороны (истребителя) состоит как в выживании, так и в поражении противника. Дуэль заканчивается, если одна из сторон поразила противника или стороны исчерпали боеприпасы. Вероятности попадания описываются в виде функцийирасстояния между самолетами. Полезность исходов дуэли для первой стороны описывается таблицей
| бомбардировщик сбит | бомбардировщик уцелел |
| истребитель сбит | 0 | -1 |
| истребитель уцелел | 1 | 0 |
Каков вид усредненной полезности истребителя, если каждая из сторон может произвести один выстрел и дуэлянты не слышат выстрелов друг друга - дуэль бесшумная
Позиционная игра. Антагонистическая игра с полной информацией, в которой первым ходит первый игрок, задана деревом  Каковы размеры матрицы игры?
Каковы размеры матрицы игры?
Установить, какая матрица является нормальной формой антагонистической игры в позиционной форме, задаваемой деревом. Предполагается, что первым ходит первый игрок 
Позиционная игра. Антагонистическая игра с полной информацией, в которой первым ходит первый игрок, задана деревом  Какие стратегии образуют седловую точку ядра антагонистической игры?
Какие стратегии образуют седловую точку ядра антагонистической игры?
Укажите фигуру, соответствующую следующей игре: Ход 1. Случайно выбирается число u из множества {1,2}.Ход 2. Первый игрок, зная значение u, выбирает число x∈{1,2}. Ход 3. Второй игрок, не зная значения u и зная значение x, выбирает y∈{1,2}. После трех ходов первый игрок выигрывает у второго величину x+y, если сумма x+y четна, и проигрывает ее в противном случае
Укажите биматричную игру, для которой ситуация равновесия определяется из графика 
Какое утверждение справедливо для биматричной игры
Укажите биматричную игру, для которой ситуации равновесия определяются из графика 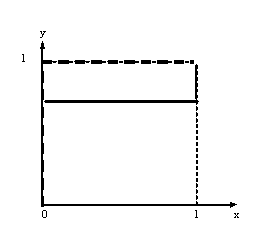
Цена игры с матрицей равна единице. Указать, какие векторы являются оптимальными по гарантированному результату стратегиями для первого игрока
Какие пары чистых стратегий игроков в биматричной игре являются эффективными, но не являются устойчивыми?
Какое решение имеет задача линейного программирования max{u1+u2:ui≥0,1≤i≤2,-u1+u2≤9, u1+2u2≤36, 2u1+u2≤42}?
Задача линейного программирования с ограничениями типа неравенств имеет вид u1*+u2*=min{u1+u2:ui≥0,1≤i≤2,u1+4u2≥1, 3u1+2u2≥1, 5u1+u2≥1}?Для какой матричной игры решение задачи линейного программирования определяет оптимальную стратегию первого игрока?
Какое решение имеет задача линейного программирования max{2u1+u2:ui≥0,1≤i≤2,-u1+u2≤9, u1+2u2≤36, 2u1+u2≤42}?
Пусть первый игрок располагает m единицами ресурса, второй – n еди-ницами, и у каждого имеется по две стратегии. Если игроки выбирают стратегии с одинаковыми номерами (например, первые), то ресурс второго игрока уменьшается на единицу. При выборе разных по номерам стратегий уменьшается на единицу ресурс первого игрока. Игра заканчивается, если один из игроков исчерпает свой ресурс. При этом первый игрок выигрывает единицу, если ресурс второго игрока равен нулю, и проигрывает единицу если равен нулю его собственный ресурс. Динамика запасов ресурса за один шаг игры описывается деревом  где (m,n) – начальные запасы ресурсов первого и второго игрока соответственно. Какой вид имеет матрица антагонистической игры, соответствующая игре в позиционной форме, при начальных запасах ресурсов (1,2)?
где (m,n) – начальные запасы ресурсов первого и второго игрока соответственно. Какой вид имеет матрица антагонистической игры, соответствующая игре в позиционной форме, при начальных запасах ресурсов (1,2)?
Игра, задаваемая биматрицей разыгрывается повторно, если игроки выбрали стратегии с несовпадающими номерами. Выигрыши игроков в повторениях суммируются, причем каждому из них известен выигрыш, полученный на первом этапе. Являются ли ситуациями равновесия в биматричной 8x8 игре (см. ответ 1 второй задачи) чистые стратегии?
Чему равны гарантированные выигрыши игроков в биматричной игре
Какой вид имеет множество допустимых сделок без побочных платежей для биматричной игры
Какой вид имеет множество допустимых сделок без побочных платежей для биматричной игры
Какой вид имеет множество допустимых сделок с побочными платежами для биматричной игры
Какая сделка (u0,v0) удовлетворяет аксиомам Нэша для допустимого множества S  при гарантированных уровнях u*=1,v*=0?
при гарантированных уровнях u*=1,v*=0?
Какая сделка u0,v0 удовлетворяет аксиомам Нэша для допустимого множества S 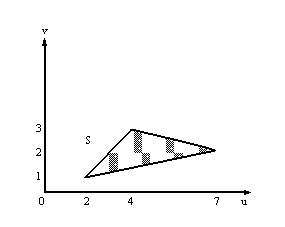 при гарантированных уровнях u*=2,v*=1?
при гарантированных уровнях u*=2,v*=1?
Задача торга. Продавец (первый игрок) располагает едини-цей неделимого товара. Он решает, какую назначить цену: высокую или низкую. Покупатель (второй игрок) может либо приобрести товар, либо отказаться от покупки. Матрицы доходов в не-которых условных единицах имеют вид  Чему равны гарантированные выигрыши сторон? Какая сделка (u0,v0) удовлетворяет аксиомам Нэша?
Чему равны гарантированные выигрыши сторон? Какая сделка (u0,v0) удовлетворяет аксиомам Нэша?
Множество допустимых сделок задачи о выпуске продукции имеет вид  Чему равны гарантированные выигрыши сторон? Какая сделка (u0,v0) удовлетворяет аксиомам Нэша?
Чему равны гарантированные выигрыши сторон? Какая сделка (u0,v0) удовлетворяет аксиомам Нэша?
Выбор маршрута. Транспортное предприятие планирует открыть автобусную линию от нового микрорайона до центра города либо по маршруту α1, либо по более протяженному маршруту α2 . Известно, что 30% жителей микрорайона работает в организациях, расположенных в окрестности маршрута α1 (первое состояние), и 70% - в окрестности маршрута α2 (второе состояние). Потери транспортного предприятия оцениваются матрицей  Пусть для обоснования решения о маршруте используются следующие результаты выборочного анкетирования о предпочтениях жителей микрорайона (в зависимости от места работы):
Пусть для обоснования решения о маршруте используются следующие результаты выборочного анкетирования о предпочтениях жителей микрорайона (в зависимости от места работы):
| z1- на работу и домой по маршруту α1 | z2 - на работу и домой по маршруту α2 | z3- на работу по маршруту α1, домой по маршруту α2 | z4 - на работу по маршруту α2, домой по маршруту α1 |
| p(z/1) | 0,5 | 0,2 | 0,2 | 0,1 |
| p(z/2) | 0,3 | 0,4 | 0,2 | 0,1 |
Чему равен риск
ρ(ξ,d) от применения решающей функции
при априорном распределении вероятностей
ξ=(0.3,0.7)?
В статистической 2x3 игре
| z1 | z2 |
| p(z/1) | 0,25 | 0,75 |
| p(z/2) | 0,75 | 0,25 |
Какое решение принять статистику, если
ξ=(0.5,0.5) и в результате эксперимента наблюдается
z2?
В статистической игре с единичным испытанием матрица потерь имеет вида статистическая связь между состояниями природы и результатами эксперимента описывается таблицей
| z1 | z2 | z3 | z4 |
| p(z/1) | 0,5 | 0,2 | 0,2 | 0,1 |
| p(z/2) | 0,3 | 0,4 | 0,2 | 0,1 |
(см. задачу о выборе маршрута, стр. 312). Функция байесовского риска состоит из четырех отрезков, принадлежащих прямым
ρ=ξ,ρ=0,5ξ+0,1(1-ξ),ρ=0,2ξ+0,2(1-ξ),ρ=1/3(1-ξ) и имеет вид

Чему равны минимаксные потери статистика?
В статистической игре с единичным испытанием матрица потерь имеет вида статистическая связь между состояниями природы и результатами эксперимента описывается таблицей
| z1 | z2 |
| p(z/1) | 0,6 | 0,4 |
| p(z/2) | 0,2 | 0,8 |
(см. задачу о выборе маршрута, стр. 312). Функция байесовского риска состоит из трех отрезков, принадлежащих прямым
ρ=ξ,ρ=0,4ξ+0,8(1-ξ),ρ=4(1-ξ) и имеет вид

Чему равны минимаксные потери статистика?
Пусть первый игрок располагает m единицами ресурса, второй – n еди-ницами, и у каждого имеется по две стратегии. Если игроки выбирают стратегии с одинаковыми номерами (например, первые), то ресурс второго игрока уменьшается на единицу. При выборе разных по номерам стратегий уменьшается на единицу ресурс первого игрока. Игра заканчивается, если один из игроков исчерпает свой ресурс. При этом первый игрок выигрывает единицу, если ресурс второго игрока равен нулю, и проигрывает единицу если равен нулю его собственный ресурс. Динамика запасов ресурса за один шаг игры описывается деревом  где (m,n) – начальные запасы ресурсов первого и второго игрока соответственно. Укажите 2x2 матрицу, соответствующую первому из двух возможных этапов игры, при начальных запасах ресурсов (1,2)
где (m,n) – начальные запасы ресурсов первого и второго игрока соответственно. Укажите 2x2 матрицу, соответствующую первому из двух возможных этапов игры, при начальных запасах ресурсов (1,2)
Какое решение имеет задача линейного программирования Указать, какую из задач линейного программирования следует решить для отыскания оптимальной по гарантированному результату стратегии второго игрока
Говорят, что стратегия x1a первого игрока является абсолютной в игре <X1,X2,M1(x1,x2),M2(x1,x2)>, если (∀x1∈X1)(∀x2∈X2)M1(x1а,x2) ≥M1(x1,x2) Какие утверждения справедливы для игры, в которой множества стратегий игроков X1={1,2,3,4}, X2={1,2,3,4,5}, а функции выигрыша заданы в виде
Антагонистическая игра задана матрицей В пользу какого игрока поставлена игра?
В статистической 2x3 игре
| z1 | z2 |
| p(z/1) | 0,25 | 0,75 |
| p(z/2) | 0,75 | 0,25 |
Какое решение принять статистику, если
ξ=(0.25,0.75) и в результате эксперимента наблюдается
z2?
Пусть биматричная 2x2 игра обладает свойством (∀(i,j)≠(k,l))(aij≠akl,bij≠bkl). Какие утверждения справедливы для этой игры?
Какой вид имеет множество допустимых сделок с побочными платежами для биматричной игры
Два производителя одного и того же товара могут производить его в объемах 0≤xi ≤1, i=1,2. Затраты на выпуск единицы продукции составляют ci(xi)=Cixi,Ci>0 Товар подается на рынке по цене p(x)=1-x, где x=x1+x2 - совокупное предложение товара. Прибыльi-го производителя от выпуска товара в объеме xi описывается функцией M1(x1,x2)=xip(x)-ci(xi). Указать, какой вид имеет график функции наилучшего ответа второго производителя на известное решение об объеме выпуска первого при C1=0,6,C2=0,4
Каждая из противоборствующих сторон пытается овладеть позицией противника. Первая сторона располагает двумя подразделениями, вторая – одним подразделением. Силы сторон распределяются для обороны собственной позиции и атаки позиции противника. Позиция считается занятой той стороной, которая выделила для ее захвата большее (целое) число подразделений. Если атакующие силы недостаточны для захвата позиций, то они отступают, и игра начинается заново. Игра завершается, если захвачена одна из позиций. Примем, что интересы сторон противоположны. При этом первая сторона выигрывает единицу, если ей удалось завладеть позицией противника, не потеряв своей, и проигрывает единицу, потеряв свой лагерь. Если в течение T периодов столкновений ни одна из позиций не захвачена, то игра завершается вничью. Для случая Т=2 дерево игры имеет вид  где пара (i,j) означает "оставить i подразделений для обороны и направить j подразделений для атаки". Установить, какая из матриц является нормальной формой антагонистической игры в позиционной форме, соответствующей случаю Т=2
где пара (i,j) означает "оставить i подразделений для обороны и направить j подразделений для атаки". Установить, какая из матриц является нормальной формой антагонистической игры в позиционной форме, соответствующей случаю Т=2

Дуополия с назначением выпусков. Два производителя одного и того же товара могут производить его в объемах 0≤xi≤0.5, i=1,2. Затраты на выпуск единицы продукции составляют ci(xi)=Cixi,Ci>0. Товар подается на рынке по цене p(x)=1-x, где x=x1+x2 - совокупное предложение товара. Прибыль i-го производителя от выпуска товара в объеме xi описывается функцией Mi(xix2)=xip(x)-ci(xi). Какие объемы выпуска являются устойчивыми в дуополии с назначением выпусков (образуют ситуацию равновесия по Нэшу) при C1=0,5, C2=0,5?
Какие согласованные смешанные стратегии игроков в задаче о сделке, порождаемой биматричной игрой к дележу (u,v)=(1,1)?
Какие рулетки реализуют случайный выбор с вероятностями (2/3,1/3)?
Дуэль истребитель-бомбардировщик. Пусть в дуэли истребитель-бомбардировщик самолеты летят навстречу друг другу с единичного рас-стояния, и цель второй стороны (бомбардировщика) состоит в выживании. Дуэль заканчивается, если одна из сторон поразила противника или стороны исчерпали боеприпасы. Вероятности попадания описываются в виде функцийирасстояния между самолетами. Полезность исходов дуэли для второй стороны описывается таблицей
| бомбардировщик сбит | бомбардировщик уцелел |
| истребитель сбит | 0 | 1 |
| истребитель уцелел | 0 | 1 |
Каков вид усредненной полезности бомбардировщика, если каждая из сторон может произвести один выстрел и дуэлянты слышат выстрелы друг друга - дуэль шумная
В игре двух лиц <X1,X2,M1(x1,x2),M2(x1,x2)>X1=[-1,1], X2=[0,2], M1(x1,x2)=M2(x1,x2)=-x1-x2. Какой выигрыш гарантирует первому игроку стратегия x1=0?
Пусть первый игрок располагает m единицами ресурса, второй – n еди-ницами, и у каждого имеется по две стратегии. Если игроки выбирают стратегии с одинаковыми номерами (например, первые), то ресурс второго игрока уменьшается на единицу. При выборе разных по номерам стратегий уменьшается на единицу ресурс первого игрока. Игра заканчивается, если один из игроков исчерпает свой ресурс. При этом первый игрок выигрывает единицу, если ресурс второго игрока равен нулю, и проигрывает единицу если равен нулю его собственный ресурс. Динамика запасов ресурса за один шаг игры описывается деревом  где (m,n) – начальные запасы ресурсов первого и второго игрока соответственно. Какой вид имеет матрица выигрышей первого игрока, если запас ресурсов каждого из игроков равен единице?
где (m,n) – начальные запасы ресурсов первого и второго игрока соответственно. Какой вид имеет матрица выигрышей первого игрока, если запас ресурсов каждого из игроков равен единице?
Два предприятия, обладающие производственными возможностями Ki, i=1,2, продают на рынке один и тот же вид продукции. Возможности рынка ограничены суммой денег С. Пусть xi, 0≤xi≤Ki - количество продукции, производимой предприятием i, a - себестоимость единицы продукции, pi, a≤pi≤C/xi - цена единицы продукции. Предположим, что: предприятия не знают объемов выпуска и выбираемых цен продукции друг друга; на рынке вначале покупается более дешевая продукция; случае равенства цен покупается продукция второго предприятия.Укажите вид критерия эффективности первого предприятия, если его цель состоит в получении большей прибыли, чем у партнера
Говорят, что стратегия x2′ нестрого доминирует стратегию x2" в игре <X1,X2,M1(x1,x2),M2(x1,x2)>, если (∀x1∈X1)M2(x1′,x2) >M2(x1",x2) Какие утверждения справедливы для игры, в которой множества стратегий игроков X1={1,2,3,4}, X2={1,2,3,4,5}, а функции выигрыша заданы в виде
Позиционная игра. Антагонистическая игра с полной информацией, в которой первым ходит первый игрок, задана деревом  Какие стратегии образуют седловую точку ядра антагонистической игры?
Какие стратегии образуют седловую точку ядра антагонистической игры?
Какие объемы выпуска являются устойчивыми (образуют ситуацию равновесия по Нэшу) в дуополии с назначением выпусков при C1=0,7, C2=0,7
Чему равны гарантированные выигрыши игроков в биматричной игре
Игра, задаваемая биматрицей разыгрывается повторно, если игроки выбрали стратегии с несовпадающими номерами. Выигрыши игроков в повторениях суммируются, причем каждому из них известен выигрыш, полученный на первом этапе. Являются ли ситуациями равновесия в исходной биматричной игре чистые стратегии?
Контроль качества продукции. Заказчик, осуществляя приемку у исполнителя сложного технического изделия, может выбрать одно из двух решений: признать изделие годным и принять его в эксплуатацию (покрывая стоимость обнаруженных впоследствии дефектов) либо признать изделие непригодным для эксплуатации и потребовать замены отдельных (возможно, некачественных) узлов. Качество изделия может быть удовлетворительным или неудовлетворительным, в зависимости от соблюдения технологии изготовления изделия. Замена исправных узлов оплачивается заказчиком и составляет условную единицу. Стоимость обнаруженных во время эксплуатации дефектов обходится заказчику в два раза дороже, в остальных случаях потери отсутствуют. Матрица потерь заказчика имеет вид  Отношения правдоподобия p(z/2)/p(z/1) для результатов тестирования есть
Отношения правдоподобия p(z/2)/p(z/1) для результатов тестирования есть
| z1- тестирование прошло успешно | z2 - выполнилась большая часть тестов | z3- выполнилась меньшая часть тестов | z4 - ни один из тестов не выполнился |
| p(z/2)/p(z/1) | 0 | 1/3 | 5 | ∞ |
Каков вид байесовской решающей функции при равновоз-можных состояниях природы?
Дуополия с назначением выпусков. Два производителя одного и того же товара могут производить его в объемах 0≤xi≤0.5, i=1,2. Затраты на выпуск единицы продукции составляют ci(xi)=Cixi,Ci>0. Товар подается на рынке по цене p(x)=1-x, где x=x1+x2 - совокупное предложение товара. Прибыль i-го производителя от выпуска товара в объеме xi описывается функцией Mi(xix2)=xip(x)-ci(xi). Какие объемы выпуска являются оптимальными по Парето (эффективными) в дуополии с назначением выпусков при C1=0,4, C2=0,4
Цена игры с матрицей равна нулю. Указать, какие вектора являются оптимальными по гарантированному результату стратегиями для второго игрока
Рынок товара. Зависимость спроса на однородный товар от цены p за единицу товара имеет вид Поступление товара на рынок описывается функцией предложения pmin=2, pmax=12. Пусть посредник при понижении цены осуществляет закупку двух единиц товара, которые сбываются при повышении цены. Чему равна прибыль посредника в результате операции купли-продажи, если в начальный момент времени p=10,5, S(10,5)=17?
Пусть в игре двух лиц <X1,X2,M1 (x1,x2),M2(x1,x2)> множества стратегий конечны X1=X2={1,2} и порядок ходов заранее не определен. Игроку, делающему ход вторым, известен выбор партнера. В какой из игр возникает борьба за право второго хода?
Рынок товара. Зависимость спроса на однородный товар от цены p за единицу товара имеет вид Поступление товара на рынок описывается функцией предложения pmin=2, pmax=12 При какой цене товара имеет баланс спроса и предложения?
Рынок товара. Зависимость спроса на однородный товар от цены p за единицу товара имеет видПоступление товара на рынок описывается функцией предложения pmin=2, pmax=12. Является ли цена, определяющая равновесие спроса и предложения, устойчивой, если количество товара, поступающего на рынок в текущий момент, определяется ценой товара в предшествующий момент дискретного времени?
Какому типу принадлежит игра <X,Y,M1(x,y),M2 (x, y)>, в которой X={x:0≤x≤1},Y={y:0≤y≤1}
Установить, какие точки являются седловыми для функции M(x,y)=8xy-4x-4y+1 в области 0≤x≤1,0≤y≤1
Какие пары стратегий являются седловыми точками матричной игры
Какие пары стратегий являются седловыми точками матричной игры
Какое решение имеет задача линейного программирования max{-u1+2u2:ui≥0,1≤i≤2,-u1+u2≤9, u1+2u2≤36, 2u1+u2≤42}?
Каждая из противоборствующих сторон пытается овладеть позицией противника. Первая сторона располагает двумя подразделениями, вторая – одним подразделением. Силы сторон распределяются для обороны собственной позиции и атаки позиции противника. Позиция считается занятой той стороной, которая выделила для ее захвата большее (целое) число подразделений. Если атакующие силы недостаточны для захвата позиций, то они отступают, и игра начинается заново. Игра завершается, если захвачена одна из позиций. Примем, что интересы сторон противоположны. При этом первая сторона выигрывает единицу, если ей удалось завладеть позицией противника, не потеряв своей, и проигрывает единицу, потеряв свой лагерь. Если в течение T периодов столкновений ни одна из позиций не захвачена, то игра завершается вничью. Для случая Т=2 дерево игры имеет вид  где пара (i,j) означает "оставить i подразделений для обороны и направить j подразделений для атаки".Укажите матрицу, которая является нормальной формой антагонистической игры в позиционной форме, соответствующей случаю Т=1
где пара (i,j) означает "оставить i подразделений для обороны и направить j подразделений для атаки".Укажите матрицу, которая является нормальной формой антагонистической игры в позиционной форме, соответствующей случаю Т=1

Какой вид имеет паретовская граница множества S?
Какой вид имеет множество допустимых сделок с побочными платежами для биматричной игры
Задача торга. Продавец (первый игрок) располагает едини-цей неделимого товара. Он решает, какую назначить цену: высокую или низкую. Покупатель (второй игрок) может либо приобрести товар, либо отказаться от покупки. Матрицы доходов в не-которых условных единицах имеют вид  Как выглядят оптимальные стратегии угроз при заключении сделки и какую сделку (u+,v+) они порождают?
Как выглядят оптимальные стратегии угроз при заключении сделки и какую сделку (u+,v+) они порождают?
В статистической игре с единичным испытанием матрица потерь имеет вида статистическая связь между состояниями природы и результатами эксперимента описывается таблицей
| z1 | z2 |
| p(z/1) | 0,6 | 0,4 |
| p(z/2) | 0,2 | 0,8 |
(см. задачу о выборе маршрута, стр. 312). Функция байесовского риска состоит из трех отрезков, принадлежащих прямым
ρ=ξ,ρ=0,4ξ+0,8(1-ξ),ρ=4(1-ξ) и имеет вид

Какая стратегия статистика является минимаксной?
В статистической игре с единичным испытанием матрица потерь имеет вид а статистическая связь между состояниями природы и результатами эксперимента описывается таблицей
| z1 | z2 | z3 | z4 |
| p(z/1) | 0,6 | 0,3 | 0,1 | 0 |
| p(z/2) | 0 | 0,1 | 0,5 | 0,4 |
(см. задачу контроля качества продукции). Функция байесовского риска состоит из трех отрезков, принадлежащих прямым
ρ=0,4ξ,ρ=0,1ξ+0,1(1-ξ)2,ρ=0,6ξ(1-ξ)2 и имеет вид
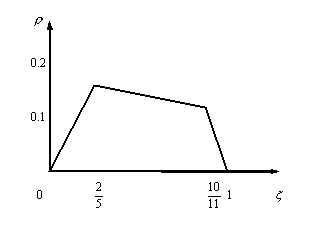
Чему равны минимаксные потери статистика?
Рынок товара. Зависимость спроса на однородный товар от цены p за единицу товара имеет вид Поступление товара на рынок описывается функцией предложения pmin=2, pmax=12. Является ли цена, определяющая равновесие спроса и предложения, устойчивой, если количество товара, поступающего на рынок в текущий момент, определяется ценой товара в предшествующий момент дискретного времени?
Антагонистическая игра задана матрицей Указать, какую задачу линейного программирования следует решить для отыскания цены игры
Две конкурирующие фирмы производят сезонный товар, пользующийся спросом в период времени 0≤t≤1. Качество конкурирующих товаров зависит от времени их поступления на рынок - чем позже товар появляется на рынке, тем качество его выше. Примем, что покупатели при отсутствии конкуренции приобретают товар, имеющийся на рынке, а при наличии двух товаров отдают предпочтение товару более высокого качества. Если товары поступают на рынок одновременно, то они пользуются одинаковым спросом. Продажа товара приносит производителю доход С в единицу времени.Каким выражением описывается критерий эффективности первой стороны, если ее цель состоит в разорении конкурент?
Какая согласованная смешанная стратегия игроков в задаче о сделке, порождаемой биматричной игрой приводит к дележу (u,v)=(5,3)
Фрахт судна. Грузоотправитель пытается договориться с судовладельцем о фрахте судна для перевозки скоропортящейся продукции. У каждого из партнеров две стратегии: "уступка" и "непреклонность" в цене фрахта. Доходы сторон в некоторых условных единицах описываются матрицами (грузоотправитель - первый игрок) Какие решения сторон образуют ситуации равновесия по Нэшу и к каким выигрышам приводит применение равновесных стратегий?
Какие решения сторон образуют ситуации равновесия по Нэшу и к каким выигрышам приводит применение равновесных стратегий?
Установить, какая матрица является нормальной формой антагонистической игры в позиционной форме, задаваемой деревом  Предполагается, что вначале бросается симметричная монета, после чего ходит второй игрок
Предполагается, что вначале бросается симметричная монета, после чего ходит второй игрок
Укажите смешанные стратегии, являющиеся ситуациями равновесия в биматричной игре
В статистической игре с единичным испытанием матрица потерь имеет статистическая связь между состояниями природы и результатами эксперимента описывается таблицей
| z1 | z2 | z3 | z4 |
| p(z/1) | 0,5 | 0,2 | 0,2 | 0,1 |
| p(z/2) | 0,3 | 0,4 | 0,2 | 0,1 |
(см. задачу о выборе маршрута, стр. 312). Функция байесовского риска состоит из четырех отрезков, принадлежащих прямым
ρ=ξ,ρ=0,5ξ+0,1(1-ξ),ρ=0,2ξ+0,2(1-ξ),ρ=1/3(1-ξ) и имеет вид

Какая стратегия статистика является минимаксной?
Установить, какая матрица является нормальной формой антагонистической игры в позиционной форме, задаваемой деревом  Предполагается, что первым ходит первый игрок
Предполагается, что первым ходит первый игрок
Антагонистическая игра задана матрицей Указать, какую из задач линейного программирования следует решить для отыскания оптимальной по гарантированному результату стратегии первого игрока:
Выберите правильное утверждение: пара стратегий (x1,x2) называется оптимальной по Парето в игре <X1,X2,M1(x1,x2), M2(x1,x2)>, если
Установить, какие точки являются седловыми для функции M(x,y)=x-y в области 0≤x≤1,0≤y≤1?
Чему равен минимальный гарантированный проигрыш второго игрока в антагонистической игре с ядром M(x,y)=(x-y)2 и множествами стратегий -1≤x≤1,-1≤y≤1?
Дуэль истребитель-бомбардировщик. Пусть в дуэли истребитель-бомбардировщик самолеты летят навстречу друг другу с единичного рас-стояния, и цель первой стороны (истребителя) состоит как в выживании, так и в поражении противника. Дуэль заканчивается, если одна из сторон поразила противника или стороны исчерпали боеприпасы. Вероятности попадания описываются в виде функцийирасстояния между самолетами. Полезность исходов дуэли для первой стороны описывается таблицей
| бомбардировщик сбит | бомбардировщик уцелел |
| истребитель сбит | 0 | -1 |
| истребитель уцелел | 1 | 0 |
Каков вид усредненной полезности истребителя, если каждая из сторон может произвести один выстрел и дуэлянты слышат выстрелы друг друга - дуэль шумная?
Позиционная игра. Антагонистическая игра с полной информацией задана деревом  Игра начинается с бросания жребия для определения порядка ходов игроков: при выпадении единицы первым ходит первый игрок, при выпадении двойки - второй. Какие стратегии образуют седловую точку ядра антагонистической игры?
Игра начинается с бросания жребия для определения порядка ходов игроков: при выпадении единицы первым ходит первый игрок, при выпадении двойки - второй. Какие стратегии образуют седловую точку ядра антагонистической игры?
Игра, задаваемая биматрицей разыгрывается повторно, если игроки выбрали стратегии с несовпадающими номерами. Выигрыши игроков в повторениях суммируются, причем каждому из них известен выигрыш, полученный на первом этапе. Какой вид имеет биматрица игры, соответствующая повторно разыгрываемой исходной игре?
Чему равны гарантированные выигрыши игроков в биматричной игре
Какая сделка u0,v0 удовлетворяет аксиомам Нэша для допустимого множества S 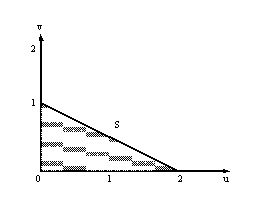 при гарантированных уровнях u*=0,v*=0?
при гарантированных уровнях u*=0,v*=0?
Выпуск продукции. Два предприятия специализируются на выпуске одного из двух видов взаимодополняющей продукции (например, первое предприятие выпускает преимущественно столы, а второе - стулья). Каждое из предприятий может выпускать продукцию типов "М" или "К" (мало- или крупногабаритную). В зависимости от выбранных решений, ожидаемые доходы от реализации в некоторых условных единицах описываются матрицами  Какие решения сторон образуют ситуацию равновесия по Нэшу и к каким выигрышам приводит применение равновесных стратегий?
Какие решения сторон образуют ситуацию равновесия по Нэшу и к каким выигрышам приводит применение равновесных стратегий?
В статистической игре с единичным испытанием матрица потерь имеет вид а статистическая связь между состояниями природы и результатами эксперимента описывается таблицей
| z1 | z2 | z3 | z4 |
| p(z/1) | 0,6 | 0,3 | 0,1 | 0 |
| p(z/2) | 0 | 0,1 | 0,5 | 0,4 |
(см. задачу контроля качества продукции, стр. 310). Функция байесовского риска состоит из трех отрезков, принадлежащих прямым
ρ=0,4ξ,ρ=0,1ξ+0,1(1-ξ)2,ρ=0,6ξ(1-ξ)2 и имеет вид

Какая стратегия статистика является минимаксной?
Две противоборствующие стороны пытаются овладеть двумя позициями. Для этого первая сторона располагает тремя подразделениями, вторая - четырьмя подразделениями (например, полками). Каждый из противников может выделить для захвата любой из позиций целое число подразделений (в том числе и нулевое), полностью расходуя ресурсы. Позиция считается занятой той стороной, которая выделила для ее захвата большее число подразделений. Какой вид имеет критерий эффективности первой стороны, если ее цель состоит в захвате максимального числа позиций
Какой вид имеет множество допустимых сделок без побочных платежей для биматричной игры
Какому типу принадлежит игра <X,Y,M1(x, y),M2 (x, y)>, в которой X={x:0≤x≤1},Y={y:0≤y≤1}
В какой из матричных игр оптимальные стратегии такие же, как и в игре с матрицей
Два производителя одного и того же товара могут производить его в объемах 0≤xi≤1, i=1,2. Затраты на выпуск единицы продукции составляют cixi=Cixi,Ci>0 Товар подается на рынке по цене p(x)=1-x, где x=x1+x2 - совокупное предложение товара. Прибыль i-го производителя от выпуска товара в объеме xi описывается функцией M1(x1,x2)=xip(x)-ci(xi). Какое решение об объеме выпуска следует принять первому производителю, обладающим правом первого хода, если второй использует в качестве ответа функцию x2=0,3-x1/2 при C1=0,6,C2=0,4?
Пусть в игре двух лиц <X1,X2,M1 (x1,x2),M2(x1,x2)> множества стратегий конечны X1=X2={1,2}, а критерии заданы в виде 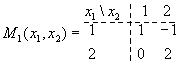
 Какое из утверждений справедливо, если игрокам известны критерии, множества стратегий и первым ходит второй игрок (случай несимметричного распределения информации об игре)?
Какое из утверждений справедливо, если игрокам известны критерии, множества стратегий и первым ходит второй игрок (случай несимметричного распределения информации об игре)?
Рынок товара. Зависимость спроса на однородный товар от цены p за единицу товара имеет вид Поступление товара на рынок описывается функцией предложения pmin=2, pmax=12. Является ли цена, определяющая равновесие спроса и предложения, устойчивой, если количество товара, поступающего на рынок в текущий момент, определяется ценой товара в предшествующий момент дискретного времени?
Укажите деревья, являющиеся позиционной формой антагонистической игры
Какие рулетки реализуют случайный выбор с вероятностями (1/8,7/8)?
Множество допустимых сделок задачи о выпуске продукции имеет вид  Как выглядят оптимальные стратегии угроз при заключении сделки и какую сделку (u+,v+) они порождают?
Как выглядят оптимальные стратегии угроз при заключении сделки и какую сделку (u+,v+) они порождают?
Рынок товара. Зависимость спроса на однородный товар от цены p за единицу товара имеет вид Поступление товара на рынок описывается функцией предложения pmin=2, pmax=12. При какой цене товара имеет баланс спроса и предложения?
В игре двух лиц <X1,X2,M1(x1,x2),M2(x1,x2)> X1=[-1,1], X2=[0,2], M1(x1,x2)=M2(x1,x2)=-x1-x2. Какой выигрыш гарантирует первому игроку стратегия x2=1?
Два предприятия, обладающие производственными возможностями Ki, i=1,2, продают на рынке один и тот же вид продукции. Возможности рынка ограничены суммой денег С. Пусть xi, 0≤xi≤Ki - количество продукции, производимой предприятием i,, a - себестоимость единицы продукции, pi, a≤pi≤C/xi - цена единицы продукции. Предположим, что: предприятия не знают объемов выпуска и выбираемых цен продукции друг друга; на рынке вначале покупается более дешевая продукция; в случае равенства цен покупается продукция второго предприятия.Как выглядит критерий эффективности первого предприятия, стремящегося получить наибольшую прибыль?
Укажите биматричную игру, для которой ситуации равновесия определяются из графика 
Укажите вектора, являющиеся смешанными стратегиями первого игрока в игре
Задача торга. Продавец (первый игрок) располагает едини-цей неделимого товара. Он решает, какую назначить цену: высокую или низкую. Покупатель (второй игрок) может либо приобрести товар, либо отказаться от покупки. Матрицы доходов в не-которых условных единицах имеют вид  Какие решения сторон образуют ситуацию равновесия по Нэшу и к каким выигрышам приводит применение равновесных стратегий?
Какие решения сторон образуют ситуацию равновесия по Нэшу и к каким выигрышам приводит применение равновесных стратегий?
Какой из наборов является решением игры с матрицей
Пусть в конечной игре двух лиц <X1,X2,M1(x1,x2),M2(x1,x2)> X1={1,2,3,4}, X1={1,2,3,4,5} Какая стратегия первого игрока является наилучшей по гарантированному результату?
Дуэль истребитель-бомбардировщик. Пусть в дуэли истребитель-бомбардировщик самолеты летят навстречу друг другу с единичного рас-стояния, и цель первой стороны (истребителя) состоит в поражении противника. Дуэль заканчивается, если одна из сторон поразила противника или стороны исчерпали боеприпасы. Вероятности попадания описываются в виде функций p1(x) и p2(y) расстояния между самолетами. Полезность исходов дуэли для первой стороны описывается таблицей
| бомбардировщик сбит | бомбардировщик уцелел |
| истребитель сбит | 1 | 0 |
| истребитель уцелел | 1 | 0 |
Каков вид усредненной полезности истребителя, если каждая из сторон может произвести один выстрел и дуэлянты не слышат выстрелов друг друга - дуэль бесшумная?
Позиционная игра. Антагонистическая игра с полной информацией задана деревом  Игра начинается с бросания жребия для определения порядка ходов игроков: при выпадении единицы первым ходит первый игрок, при выпадении двойки - второй. Каковы размеры матрицы игры?
Игра начинается с бросания жребия для определения порядка ходов игроков: при выпадении единицы первым ходит первый игрок, при выпадении двойки - второй. Каковы размеры матрицы игры?

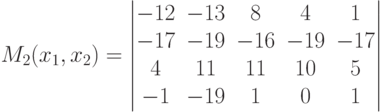
 Каковы размеры матрицы игры?
Каковы размеры матрицы игры? Пусть заказчик перед принятием решения о приемке изделия проводит тестирование изделия. Результаты тестирования зависят от качества изделия и описываются условными распределениями вероятностей
Пусть заказчик перед принятием решения о приемке изделия проводит тестирование изделия. Результаты тестирования зависят от качества изделия и описываются условными распределениями вероятностей 
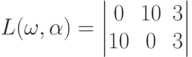
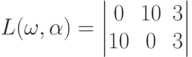
 где пара (i,j) означает "оставить i подразделений для обороны и направить j подразделений для атаки". Установите, какая 2x2 матрица описывает выигрыши первой стороны в первом из двух возможных периодов игры
где пара (i,j) означает "оставить i подразделений для обороны и направить j подразделений для атаки". Установите, какая 2x2 матрица описывает выигрыши первой стороны в первом из двух возможных периодов игры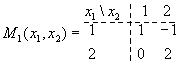
 Какое из утверждений справедливо, если игрокам известны критерии, множества стратегий и решения принимаются одновременно (случай симметричного распределения информации об игре)?
Какое из утверждений справедливо, если игрокам известны критерии, множества стратегий и решения принимаются одновременно (случай симметричного распределения информации об игре)? Графики функций математического ожидания потерь (функций риска) ρ=ρ(ξαi),1≤i≤3 в зависимости от априорного распределения вероятностей ζ=(ζ,1-ζ),0≤ζ≤1 на состояниях природы {плохая, хорошая}={1, 2} имеют вид
Графики функций математического ожидания потерь (функций риска) ρ=ρ(ξαi),1≤i≤3 в зависимости от априорного распределения вероятностей ζ=(ζ,1-ζ),0≤ζ≤1 на состояниях природы {плохая, хорошая}={1, 2} имеют вид  Пусть в задаче обслуживания загородных маршрутов диспетчер принимает решение с учетом показаний барометра, причем, в силу несовершенства прибора, показания {дождь, переменно, ясно, очень сухо}={z1,z2,z3,z4} связаны с состоянием погоды стохастически:
Пусть в задаче обслуживания загородных маршрутов диспетчер принимает решение с учетом показаний барометра, причем, в силу несовершенства прибора, показания {дождь, переменно, ясно, очень сухо}={z1,z2,z3,z4} связаны с состоянием погоды стохастически: Отношения правдоподобия p(z/2)/p(z/1) для результатов тестирования в задаче о выборе маршрута описываются таблицей
Отношения правдоподобия p(z/2)/p(z/1) для результатов тестирования в задаче о выборе маршрута описываются таблицей 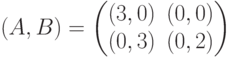 являются устойчивыми и не являются эффективными?
являются устойчивыми и не являются эффективными?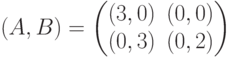
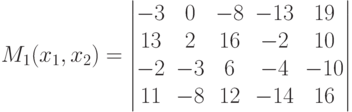
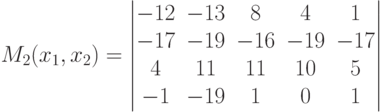
 Пусть при решении проблемы выбора участков земли для посадки используется дополнительная информация о состоянии природы, полученная в результате наблюдений за погодой весной, в период посадки. Результаты наблюдений на основе многолетней статистики определяют условные распределения (в зависимости от состояния природы)
Пусть при решении проблемы выбора участков земли для посадки используется дополнительная информация о состоянии природы, полученная в результате наблюдений за погодой весной, в период посадки. Результаты наблюдений на основе многолетней статистики определяют условные распределения (в зависимости от состояния природы) 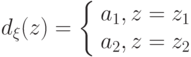
 Графики функций математического ожидания потерь (функций риска) ρ=ρ(ξαi),1≤i≤3 в зависимости от априорного распределения вероятностей ζ=(ζ,1-ζ),0≤ζ≤1 на состояниях природы {плохая, хорошая}={1, 2} имеют вид
Графики функций математического ожидания потерь (функций риска) ρ=ρ(ξαi),1≤i≤3 в зависимости от априорного распределения вероятностей ζ=(ζ,1-ζ),0≤ζ≤1 на состояниях природы {плохая, хорошая}={1, 2} имеют вид  Пусть априорное распределение вероятностей на состояниях природы в задаче обслуживания загородных маршрутов есть ξ=(1/2,1/2) (состояния природы равновозможны), и выбору решения предшествует эксперимент. Какая из решающих функций, d1 или d2, указанных в таблице, предпочтительнее?
Пусть априорное распределение вероятностей на состояниях природы в задаче обслуживания загородных маршрутов есть ξ=(1/2,1/2) (состояния природы равновозможны), и выбору решения предшествует эксперимент. Какая из решающих функций, d1 или d2, указанных в таблице, предпочтительнее?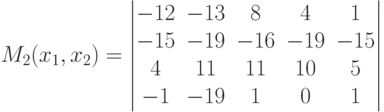 Укажите стратегии второго игрока, являющиеся наилучшими по гарантированному результату
Укажите стратегии второго игрока, являющиеся наилучшими по гарантированному результату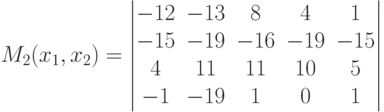
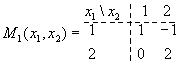
 Какое из утверждений справедливо, если игрокам известны критерии, множества стратегий и первым ходит первый игрок (случай несимметричного распределения информации об игре)?
Какое из утверждений справедливо, если игрокам известны критерии, множества стратегий и первым ходит первый игрок (случай несимметричного распределения информации об игре)? Поступление товара на рынок описывается функцией предложения
Поступление товара на рынок описывается функцией предложения  pmin=2, pmax=12. Пусть посредник при понижении цены осуществляет закупку двух единиц товара, которые сбывает при повышении цены. Чему равна прибыль посредника в результате операции купли-продажи, если в начальный момент времени p=8, S(8)=18?
pmin=2, pmax=12. Пусть посредник при понижении цены осуществляет закупку двух единиц товара, которые сбывает при повышении цены. Чему равна прибыль посредника в результате операции купли-продажи, если в начальный момент времени p=8, S(8)=18?

 Поступление товара на рынок описывается функцией предложения
Поступление товара на рынок описывается функцией предложения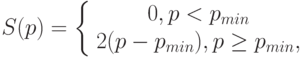 pmin=2, pmax=12. При какой цене товара имеет баланс спроса и предложения?
pmin=2, pmax=12. При какой цене товара имеет баланс спроса и предложения?
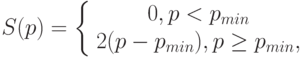
 Поступление товара на рынок описывается функцией предложения
Поступление товара на рынок описывается функцией предложения 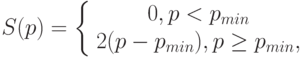 pmin=2, pmax=12. Пусть посредник при понижении цены осуществляет закупку двух единиц товара, которые сбывает при повышении цены. Чему равна прибыль посредника в результате операции купли-продажи, если в начальный момент времени p=8, S(8)=12
pmin=2, pmax=12. Пусть посредник при понижении цены осуществляет закупку двух единиц товара, которые сбывает при повышении цены. Чему равна прибыль посредника в результате операции купли-продажи, если в начальный момент времени p=8, S(8)=12
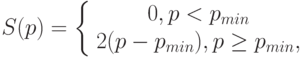
 и множествами стратегий 0≤x≤1, 0≤y≤1?
и множествами стратегий 0≤x≤1, 0≤y≤1?
 Каковы размеры матрицы игры?
Каковы размеры матрицы игры?
 Какие стратегии образуют седловую точку ядра антагонистической игры?
Какие стратегии образуют седловую точку ядра антагонистической игры?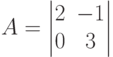 равна единице. Указать, какие векторы являются оптимальными по гарантированному результату стратегиями для первого игрока
равна единице. Указать, какие векторы являются оптимальными по гарантированному результату стратегиями для первого игрока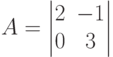
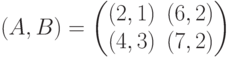 являются эффективными, но не являются устойчивыми?
являются эффективными, но не являются устойчивыми?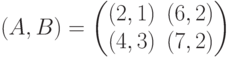
 где (m,n) – начальные запасы ресурсов первого и второго игрока соответственно. Какой вид имеет матрица антагонистической игры, соответствующая игре в позиционной форме, при начальных запасах ресурсов (1,2)?
где (m,n) – начальные запасы ресурсов первого и второго игрока соответственно. Какой вид имеет матрица антагонистической игры, соответствующая игре в позиционной форме, при начальных запасах ресурсов (1,2)?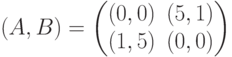 разыгрывается повторно, если игроки выбрали стратегии с несовпадающими номерами. Выигрыши игроков в повторениях суммируются, причем каждому из них известен выигрыш, полученный на первом этапе. Являются ли ситуациями равновесия в биматричной 8x8 игре (см. ответ 1 второй задачи) чистые стратегии?
разыгрывается повторно, если игроки выбрали стратегии с несовпадающими номерами. Выигрыши игроков в повторениях суммируются, причем каждому из них известен выигрыш, полученный на первом этапе. Являются ли ситуациями равновесия в биматричной 8x8 игре (см. ответ 1 второй задачи) чистые стратегии?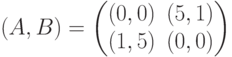
 при гарантированных уровнях u*=1,v*=0?
при гарантированных уровнях u*=1,v*=0? при гарантированных уровнях u*=2,v*=1?
при гарантированных уровнях u*=2,v*=1? Чему равны гарантированные выигрыши сторон? Какая сделка (u0,v0) удовлетворяет аксиомам Нэша?
Чему равны гарантированные выигрыши сторон? Какая сделка (u0,v0) удовлетворяет аксиомам Нэша? Чему равны гарантированные выигрыши сторон? Какая сделка (u0,v0) удовлетворяет аксиомам Нэша?
Чему равны гарантированные выигрыши сторон? Какая сделка (u0,v0) удовлетворяет аксиомам Нэша? Пусть для обоснования решения о маршруте используются следующие результаты выборочного анкетирования о предпочтениях жителей микрорайона (в зависимости от места работы):
Пусть для обоснования решения о маршруте используются следующие результаты выборочного анкетирования о предпочтениях жителей микрорайона (в зависимости от места работы):
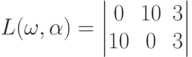
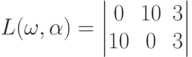
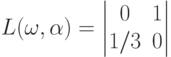 а статистическая связь между состояниями природы и результатами эксперимента описывается таблицей
а статистическая связь между состояниями природы и результатами эксперимента описывается таблицей 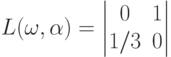
 Чему равны минимаксные потери статистика?
Чему равны минимаксные потери статистика?
 а статистическая связь между состояниями природы и результатами эксперимента описывается таблицей
а статистическая связь между состояниями природы и результатами эксперимента описывается таблицей 
 Чему равны минимаксные потери статистика?
Чему равны минимаксные потери статистика?
 где (m,n) – начальные запасы ресурсов первого и второго игрока соответственно. Укажите 2x2 матрицу, соответствующую первому из двух возможных этапов игры, при начальных запасах ресурсов (1,2)
где (m,n) – начальные запасы ресурсов первого и второго игрока соответственно. Укажите 2x2 матрицу, соответствующую первому из двух возможных этапов игры, при начальных запасах ресурсов (1,2)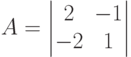 Указать, какую из задач линейного программирования следует решить для отыскания оптимальной по гарантированному результату стратегии второго игрока
Указать, какую из задач линейного программирования следует решить для отыскания оптимальной по гарантированному результату стратегии второго игрока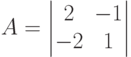
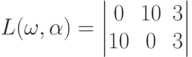
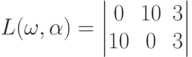
 где пара (i,j) означает "оставить i подразделений для обороны и направить j подразделений для атаки". Установить, какая из матриц является нормальной формой антагонистической игры в позиционной форме, соответствующей случаю Т=2
где пара (i,j) означает "оставить i подразделений для обороны и направить j подразделений для атаки". Установить, какая из матриц является нормальной формой антагонистической игры в позиционной форме, соответствующей случаю Т=2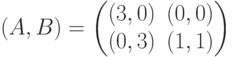 к дележу (u,v)=(1,1)?
к дележу (u,v)=(1,1)?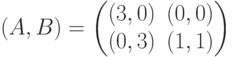
 где (m,n) – начальные запасы ресурсов первого и второго игрока соответственно. Какой вид имеет матрица выигрышей первого игрока, если запас ресурсов каждого из игроков равен единице?
где (m,n) – начальные запасы ресурсов первого и второго игрока соответственно. Какой вид имеет матрица выигрышей первого игрока, если запас ресурсов каждого из игроков равен единице?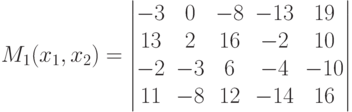

 Какие стратегии образуют седловую точку ядра антагонистической игры?
Какие стратегии образуют седловую точку ядра антагонистической игры? 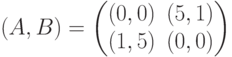 разыгрывается повторно, если игроки выбрали стратегии с несовпадающими номерами. Выигрыши игроков в повторениях суммируются, причем каждому из них известен выигрыш, полученный на первом этапе. Являются ли ситуациями равновесия в исходной биматричной игре чистые стратегии?
разыгрывается повторно, если игроки выбрали стратегии с несовпадающими номерами. Выигрыши игроков в повторениях суммируются, причем каждому из них известен выигрыш, полученный на первом этапе. Являются ли ситуациями равновесия в исходной биматричной игре чистые стратегии?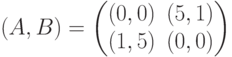
 Отношения правдоподобия p(z/2)/p(z/1) для результатов тестирования есть
Отношения правдоподобия p(z/2)/p(z/1) для результатов тестирования есть 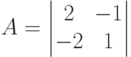 равна нулю. Указать, какие вектора являются оптимальными по гарантированному результату стратегиями для второго игрока
равна нулю. Указать, какие вектора являются оптимальными по гарантированному результату стратегиями для второго игрока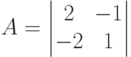
 Поступление товара на рынок описывается функцией предложения
Поступление товара на рынок описывается функцией предложения 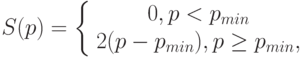 pmin=2, pmax=12. Пусть посредник при понижении цены осуществляет закупку двух единиц товара, которые сбываются при повышении цены. Чему равна прибыль посредника в результате операции купли-продажи, если в начальный момент времени p=10,5, S(10,5)=17?
pmin=2, pmax=12. Пусть посредник при понижении цены осуществляет закупку двух единиц товара, которые сбываются при повышении цены. Чему равна прибыль посредника в результате операции купли-продажи, если в начальный момент времени p=10,5, S(10,5)=17?
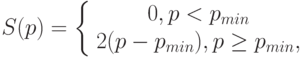
 Поступление товара на рынок описывается функцией предложения
Поступление товара на рынок описывается функцией предложения  pmin=2, pmax=12 При какой цене товара имеет баланс спроса и предложения?
pmin=2, pmax=12 При какой цене товара имеет баланс спроса и предложения?

 Поступление товара на рынок описывается функцией предложения
Поступление товара на рынок описывается функцией предложения 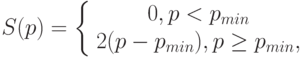 pmin=2, pmax=12. Является ли цена, определяющая равновесие спроса и предложения, устойчивой, если количество товара, поступающего на рынок в текущий момент, определяется ценой товара в предшествующий момент дискретного времени?
pmin=2, pmax=12. Является ли цена, определяющая равновесие спроса и предложения, устойчивой, если количество товара, поступающего на рынок в текущий момент, определяется ценой товара в предшествующий момент дискретного времени?
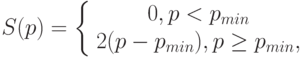
 где пара (i,j) означает "оставить i подразделений для обороны и направить j подразделений для атаки".Укажите матрицу, которая является нормальной формой антагонистической игры в позиционной форме, соответствующей случаю Т=1
где пара (i,j) означает "оставить i подразделений для обороны и направить j подразделений для атаки".Укажите матрицу, которая является нормальной формой антагонистической игры в позиционной форме, соответствующей случаю Т=1 Как выглядят оптимальные стратегии угроз при заключении сделки и какую сделку (u+,v+) они порождают?
Как выглядят оптимальные стратегии угроз при заключении сделки и какую сделку (u+,v+) они порождают? а статистическая связь между состояниями природы и результатами эксперимента описывается таблицей
а статистическая связь между состояниями природы и результатами эксперимента описывается таблицей 
 Какая стратегия статистика является минимаксной?
Какая стратегия статистика является минимаксной?
 а статистическая связь между состояниями природы и результатами эксперимента описывается таблицей
а статистическая связь между состояниями природы и результатами эксперимента описывается таблицей 
 Чему равны минимаксные потери статистика?
Чему равны минимаксные потери статистика?
 Поступление товара на рынок описывается функцией предложения
Поступление товара на рынок описывается функцией предложения  pmin=2, pmax=12. Является ли цена, определяющая равновесие спроса и предложения, устойчивой, если количество товара, поступающего на рынок в текущий момент, определяется ценой товара в предшествующий момент дискретного времени?
pmin=2, pmax=12. Является ли цена, определяющая равновесие спроса и предложения, устойчивой, если количество товара, поступающего на рынок в текущий момент, определяется ценой товара в предшествующий момент дискретного времени?

 Указать, какую задачу линейного программирования следует решить для отыскания цены игры
Указать, какую задачу линейного программирования следует решить для отыскания цены игры
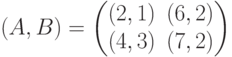 приводит к дележу (u,v)=(5,3)
приводит к дележу (u,v)=(5,3)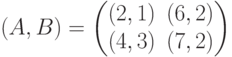
 Какие решения сторон образуют ситуации равновесия по Нэшу и к каким выигрышам приводит применение равновесных стратегий?
Какие решения сторон образуют ситуации равновесия по Нэшу и к каким выигрышам приводит применение равновесных стратегий? Предполагается, что вначале бросается симметричная монета, после чего ходит второй игрок
Предполагается, что вначале бросается симметричная монета, после чего ходит второй игрок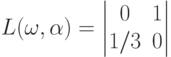 статистическая связь между состояниями природы и результатами эксперимента описывается таблицей
статистическая связь между состояниями природы и результатами эксперимента описывается таблицей 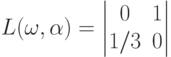
 Какая стратегия статистика является минимаксной?
Какая стратегия статистика является минимаксной?
 Предполагается, что первым ходит первый игрок
Предполагается, что первым ходит первый игрок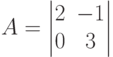 Указать, какую из задач линейного программирования следует решить для отыскания оптимальной по гарантированному результату стратегии первого игрока:
Указать, какую из задач линейного программирования следует решить для отыскания оптимальной по гарантированному результату стратегии первого игрока: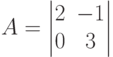
 Игра начинается с бросания жребия для определения порядка ходов игроков: при выпадении единицы первым ходит первый игрок, при выпадении двойки - второй. Какие стратегии образуют седловую точку ядра антагонистической игры?
Игра начинается с бросания жребия для определения порядка ходов игроков: при выпадении единицы первым ходит первый игрок, при выпадении двойки - второй. Какие стратегии образуют седловую точку ядра антагонистической игры?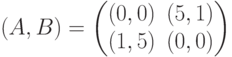 разыгрывается повторно, если игроки выбрали стратегии с несовпадающими номерами. Выигрыши игроков в повторениях суммируются, причем каждому из них известен выигрыш, полученный на первом этапе. Какой вид имеет биматрица игры, соответствующая повторно разыгрываемой исходной игре?
разыгрывается повторно, если игроки выбрали стратегии с несовпадающими номерами. Выигрыши игроков в повторениях суммируются, причем каждому из них известен выигрыш, полученный на первом этапе. Какой вид имеет биматрица игры, соответствующая повторно разыгрываемой исходной игре?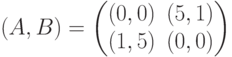
 при гарантированных уровнях u*=0,v*=0?
при гарантированных уровнях u*=0,v*=0? Какие решения сторон образуют ситуацию равновесия по Нэшу и к каким выигрышам приводит применение равновесных стратегий?
Какие решения сторон образуют ситуацию равновесия по Нэшу и к каким выигрышам приводит применение равновесных стратегий? а статистическая связь между состояниями природы и результатами эксперимента описывается таблицей
а статистическая связь между состояниями природы и результатами эксперимента описывается таблицей 
 Какая стратегия статистика является минимаксной?
Какая стратегия статистика является минимаксной?
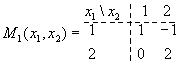
 Какое из утверждений справедливо, если игрокам известны критерии, множества стратегий и первым ходит второй игрок (случай несимметричного распределения информации об игре)?
Какое из утверждений справедливо, если игрокам известны критерии, множества стратегий и первым ходит второй игрок (случай несимметричного распределения информации об игре)? Поступление товара на рынок описывается функцией предложения
Поступление товара на рынок описывается функцией предложения 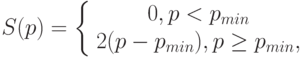 pmin=2, pmax=12. Является ли цена, определяющая равновесие спроса и предложения, устойчивой, если количество товара, поступающего на рынок в текущий момент, определяется ценой товара в предшествующий момент дискретного времени?
pmin=2, pmax=12. Является ли цена, определяющая равновесие спроса и предложения, устойчивой, если количество товара, поступающего на рынок в текущий момент, определяется ценой товара в предшествующий момент дискретного времени?
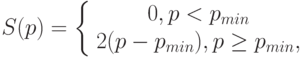
 Как выглядят оптимальные стратегии угроз при заключении сделки и какую сделку (u+,v+) они порождают?
Как выглядят оптимальные стратегии угроз при заключении сделки и какую сделку (u+,v+) они порождают? Поступление товара на рынок описывается функцией предложения
Поступление товара на рынок описывается функцией предложения 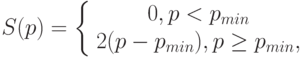 pmin=2, pmax=12. При какой цене товара имеет баланс спроса и предложения?
pmin=2, pmax=12. При какой цене товара имеет баланс спроса и предложения?
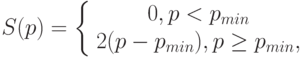
 Какие решения сторон образуют ситуацию равновесия по Нэшу и к каким выигрышам приводит применение равновесных стратегий?
Какие решения сторон образуют ситуацию равновесия по Нэшу и к каким выигрышам приводит применение равновесных стратегий? Какая стратегия первого игрока является наилучшей по гарантированному результату?
Какая стратегия первого игрока является наилучшей по гарантированному результату?