В соответствии со свойствами квантовой механики формула 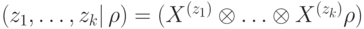 равна:
равна:
(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
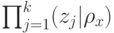 (Верный ответ)
(Верный ответ)
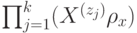 (Верный ответ)
(Верный ответ)
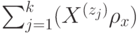

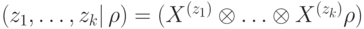 равна:
равна: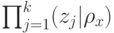 (Верный ответ)
(Верный ответ)
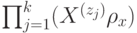 (Верный ответ)
(Верный ответ)
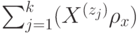
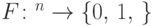 , если существует однородная последовательность квантовых схем полиномиального по
, если существует однородная последовательность квантовых схем полиномиального по  размера, реализующих такие операторы
размера, реализующих такие операторы 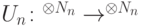 , что
, что 
 в пространство большей размерности, задаваемое формулой
в пространство большей размерности, задаваемое формулой  , матрица плотности
, матрица плотности  преобразуется:
преобразуется: , где
, где  , то вероятность наблюдения состояния
, то вероятность наблюдения состояния  можно записать в виде:
можно записать в виде: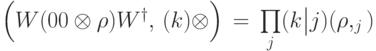 ?
? в операторе
в операторе  можно разложить в сумму проекторов на собственные подпространства следующим образом:
можно разложить в сумму проекторов на собственные подпространства следующим образом: 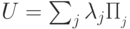 ,
,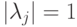 ?
? разложить
разложить  в сумму проекторов на собственные подпространства следующим образом:
в сумму проекторов на собственные подпространства следующим образом: 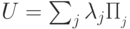 ,
,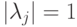 ?
?