Классические и квантовые вычисления - ответы
Количество вопросов - 336
Состояние машины Тьюринга задается тройкой 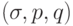 , где бесконечное слово в алфавите
, где бесконечное слово в алфавите  - это:
- это:
Какому Выберите верное утверждение:
Выберите верное утверждение:
Чему равна вероятность "события"  для квантового состояния, задаваемого матрицей плотности
для квантового состояния, задаваемого матрицей плотности  и подпространства
и подпространства  :
:
Выберите верное утверждение:
Конечному состоянию гамильтониана, сопоставляемого схеме, отвечает:
Условием строгой формулировки вычислительной задачи является наличие:
Усиление оценки вероятностей с 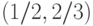 до
до 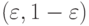 является основанием доказательства:
является основанием доказательства:
Перестановка, реализуемая обратимой схемой, является ( - некоторое множество перестановок вида
- некоторое множество перестановок вида 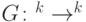 ):
):
Любой оператор, обладающий свойствами 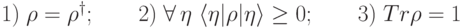
Какое значение принимает функция 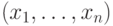 , если более половины ее аргументов равны 1:
, если более половины ее аргументов равны 1:
Верным является тождество:
Какая из ниже перечисленных формул является справедливой:
Какие свойства характерны классической вероятности:
Для тензорного произведения пространств, на которых действуют сомножители, справедливо:
Частичная функция  из
из  в
в  вычислима на машине Тьюринга :
вычислима на машине Тьюринга :
В широкий класс задач, связанных с абелевыми группами, входят задачи, открытые:
Чему равна вероятность того, что что  случайных сдвигов не покрывают фиксированный элемент, где
случайных сдвигов не покрывают фиксированный элемент, где  - некоторая группа, а
- некоторая группа, а  - подмножество
- подмножество  :
:
Величина энергии, требуемая для стирания одного бита:
Условие нормировки 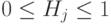 означает:
означает:
Если характеристическая функция предиката вычислима на машине Тьюринга  , для которой
, для которой 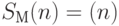 , то
, то
Проверка простоты числа является классическим примером задачи класса:
Функция  принадлежит классу NP, если есть частично определенная функция
принадлежит классу NP, если есть частично определенная функция  от двух переменных, такая что:
от двух переменных, такая что:
Условием выхода из алгоритма проверки простоты числа является:
"Если  - разложение числа на взаимно простые множители, то существует взаимно однозначное соответствие между остатками от деления на
- разложение числа на взаимно простые множители, то существует взаимно однозначное соответствие между остатками от деления на  и парами остатков от деления на
и парами остатков от деления на  и на
и на 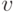 " - утверждает:
" - утверждает:
Для вероятностной машины Тьюринга можно определить:
В формуле  для нахождения количества состояний системы,
для нахождения количества состояний системы,  - это:
- это:
Авторами теоремы "Если 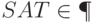 , то
, то  " являются:
" являются:
Каким равенством выражается дуальность между классическими и фазовыми ошибками?
Если кодировки переводятся друг в друга при помощи полиномального алгоритма, то они:
В наборе 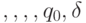 для задания машины Тьюринга выполняется условие:
для задания машины Тьюринга выполняется условие:
Для задания состояния машины Тьюринга обязательным является указание:
Условием разрешимости предиката является:
Тезисом Черча является утверждение:
Вершины входной степени 0 ориентированного ациклического графа помечаются:
Дизъюнктивной нормальной форме (ДНФ) соответствует:
Машина Тьюринга, имеющая состояния, в которых она может выполнить одно из нескольких действий, называется:
Какое понятие используется для определения класса 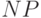 :
:
Под размером входа для предиката 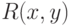 в записи
в записи 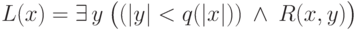 понимают:
понимают:
Если 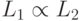 , то:
, то:
Если 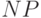 -полный предикат можно вычислить за время
-полный предикат можно вычислить за время 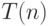 , то любой предикат из
, то любой предикат из 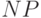 для некоторого числа
для некоторого числа  можно вычислить за время:
можно вычислить за время:
Проверка транзизитивности сводимости - если 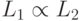 ,
, 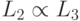 , то
, то 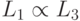 является достаточным доказательством утверждения:
является достаточным доказательством утверждения:
Если предикат  принадлежит классу BPP, то выражение
принадлежит классу BPP, то выражение 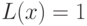 означает, что:
означает, что:
Утверждение "если  - простое и
- простое и 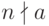 , то
, то 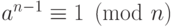 " является:
" является:
Размер схемы умножения чисел  ,
,  столбиком определяется, как:
столбиком определяется, как:
Условие 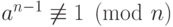 алгоритма проверки простоты числа, где
алгоритма проверки простоты числа, где  - случайное среди чисел от 1 до
- случайное среди чисел от 1 до  :
:
Алгоритм проверки простоты числа с вероятностью 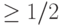 выдает ответ:
выдает ответ:
Обозначение класса дополнений классу языков  имеет вид:
имеет вид:
Автором теоремы "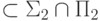 " является:
" является:
Чем объясняется то, что вероятность события ![\Prob[G\setminus\big( \bigcup_i g_iX\big)\ne\emptyset]](https://intuit.ru//sites/default/files/tex_cache/bbebb8b3a266e675f2fb0d999601618d.png) не больше
не больше 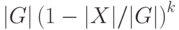 , где
, где  - некоторая группа, а
- некоторая группа, а  - подмножество
- подмножество  :
:
Функции, которые могут быть вычислены на машине Тьюринга, использующей память, ограниченную полиномом от длины входного слова относятся к классу:
Если число ходов ограничено 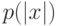 , а
, а 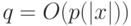 , то время работы машины Тьюринга ограничено:
, то время работы машины Тьюринга ограничено:
Выберите верное утверждение:
Задача 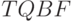 является полной задачей класса:
является полной задачей класса:
Вычислительные возможности при переходе от преобразований конечных множеств к унитарным преобразованиям конечномерных пространств:
q-бит квантового компьютера:
Выберите верное утверждение:
Определение тензорного произведения двух пространств  и
и 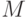 , в которых фиксированы базисы
, в которых фиксированы базисы 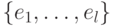 и
и 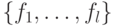 :
:
Выделенный базис для 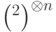 имеет вид:
имеет вид:
Обозначение скалярного произведения в гильбертовом пространстве является запись:
Элементарному преобразованию в квантовом случае соответствует определение:
Для квантовой схемы  - последовательности
- последовательности ![U_l[A_l]\cdot\ldots\cdot U_1[A_1]](https://intuit.ru//sites/default/files/tex_cache/775eb18f0bd0e4ef44cc3ecf4a874300.png) ,
, 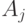 выступает в роли:
выступает в роли:
В соответствии с каким оператором действует унитарный оператор 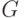 в пространстве
в пространстве 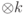 :
:
Какому условию должно удовлетворять произведение перестановок, определяющее перестановку ![W=U_l[A_l]\cdot\ldots\cdot U_1[A_1]](https://intuit.ru//sites/default/files/tex_cache/526cd679d7bedf77b6a7aab913526691.png) в расширенном смысле:
в расширенном смысле:
Какие две функции необходимо включить в базис, чтобы реализовать любую функцию:
Что означает символ  :
:
Два различных логических состояния становятся одинаковыми при выполнении:
Если существует вычисление, требующее памяти  , то реализовать его можно обратимым способом с использованием памяти:
, то реализовать его можно обратимым способом с использованием памяти:
Выберите верное утверждение:
В чем заключается проблема выбора базиса в квантовых схемах:
Оператор с квантовым управлением имеет обозначение:
Если справедливо равенство 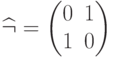 , то
, то  =:
=:
Матрицы  , образующие ортонормированный базис, называются:
, образующие ортонормированный базис, называются:
Если унитарный оператор  действует на трехмерном евклидовом пространстве (
действует на трехмерном евклидовом пространстве ( ), то задаваемый изоморфизм имеет вид:
), то задаваемый изоморфизм имеет вид:
Если унитарный оператор  действует на трехмерном евклидовом пространстве (
действует на трехмерном евклидовом пространстве ( ), для матриц Паули
), для матриц Паули  ,
,  соответствует повороту вокруг оси X на:
соответствует повороту вокруг оси X на:
Какое обозначение имеет норма вектора:
Что из ниже перечисленного характерно для смешанного состояния:
Чему равна вероятность получения базисного состояния,  при измерении состояния
при измерении состояния  :
:
Какое название имеет функция 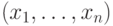 :
:
За какое время квантовый компьютер вычислит значение предиката  (
( - количество шагов):
- количество шагов):
Какой вид будет иметь запись оператора 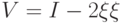 в матричной форме:
в матричной форме:
Если имеются операторы  и
и 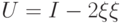 , то:
, то:
Конструктивное описание квантовой схемы формируется:
Если система из  q-битов находится в состоянии
q-битов находится в состоянии 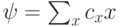 , то вероятность обнаружить систему в состоянии x определяется как:
, то вероятность обнаружить систему в состоянии x определяется как:
Какая из ниже перечисленных формул является справедливой:
Проектор на подпространство, порожденное 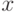 , обозначается, как:
, обозначается, как:
Что из ниже перечисленного является характерным для проекторов на подпространство
Каким условиям удовлетворяют операторы вида 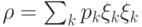 :
:
Состояние, заданное вектором (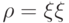 ), называется:
), называется:
Каким образом определяется частичный след оператора  по пространству
по пространству 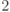 (
(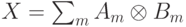 ):
):
Матрицу плотности чистого состояния 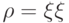 унитарный оператор переводит в матрицу:
унитарный оператор переводит в матрицу:
В случае изометрического вложение  в пространство большей размерности, задаваемое формулой
в пространство большей размерности, задаваемое формулой  , матрица плотности
, матрица плотности  преобразуется:
преобразуется:
Какие из ниже перечисленных условий являются обязательными для того, чтобы линейный оператор  являлся физически реализуемым преобразованием матриц плотности:
являлся физически реализуемым преобразованием матриц плотности:
Выполнение каких действий необходимо для доказательства физической реализации преобразования вида 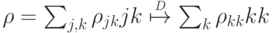 :
:
Преобразование, заключающееся в обнулении внедиагональных элементов, записывается в виде:
Если имеется физически реализуемое преобразование  , причем для любого чистого состояния
, причем для любого чистого состояния  выполняется свойство:
выполняется свойство: 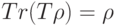 , то для любого оператора
, то для любого оператора  справедливым является равенство (
справедливым является равенство ( - некоторая фиксированная матрица плотности на пространстве
- некоторая фиксированная матрица плотности на пространстве  ):
):
При отображении  в
в  ,
,  - квантовая часть и
- квантовая часть и  - классическая часть системы, результат является диагональным по отношению:
- классическая часть системы, результат является диагональным по отношению:
В детерминированном измерении 
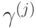 выступает в качестве:
выступает в качестве:
Какой вид имеет оператор, реализуемый квантовой схемой?
Если есть пространство состояний  , причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств:
, причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств:  , тогда всякий оператор вида
, тогда всякий оператор вида 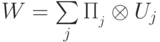 будет называться:
будет называться:
Если к состоянию, описываемому матрицей плотности  , подсоединить прибор с выделенным базисом, то совместное состояние системы и прибора будет описываться матрицей плотности вида:
, подсоединить прибор с выделенным базисом, то совместное состояние системы и прибора будет описываться матрицей плотности вида:
Почему  в операторе
в операторе  можно разложить в сумму проекторов на собственные подпространства следующим образом:
можно разложить в сумму проекторов на собственные подпространства следующим образом: 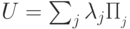 ,
,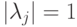 ?
?
Если унитарный оператор  разложить в сумму проекторов на собственные подпространства следующим образом:
разложить в сумму проекторов на собственные подпространства следующим образом: 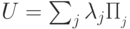 ,
,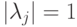 , то
, то 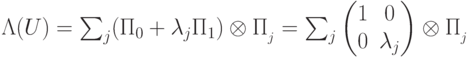 . В этом случае условные вероятности будут равны:
. В этом случае условные вероятности будут равны:
Квантовые условные вероятности 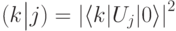 ведут себя как обычные, если...
ведут себя как обычные, если...
Продолжите фразу: условные вероятности для произведения измеряющих "разными приборами" операторов...
Верно ли, что если применить измеряющий оператор к состоянию  , где
, где  , то вероятность наблюдения состояния
, то вероятность наблюдения состояния  можно записать в виде:
можно записать в виде: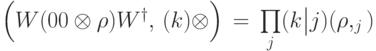 ?
?
Автором "задачи о скрытой группе" является
Какую сложность имеет алгоритм нахождения скрытой группы  :
:
Как называется порядок числа  в мультипликативной группе вычетов
в мультипликативной группе вычетов 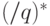
С какой вероятностью должен вычисляться делитель составного числа в подпрограмме для нахождения факторизации числа:
Если получено 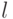 дробей вида
дробей вида  то вероятность того, что наименьшее общее кратное их знаменателей отлично от
то вероятность того, что наименьшее общее кратное их знаменателей отлично от  (равномерно распределенное на множестве
(равномерно распределенное на множестве  случайное число):
случайное число):
Какое свойство характерно для оператора умножения на число 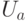
Какое из ниже перечисленных равенств является справедливым (с учетом тождества 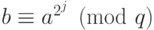 ):
):
Если требуется  обращений к оракулу и каждый вопрос имеет длину
обращений к оракулу и каждый вопрос имеет длину  , то размер квантовой схемы определяется как:
, то размер квантовой схемы определяется как:
Каким условиям должны удовлетворять операторы 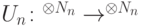 , реализуемые однородной последовательностью квантовых схем полиномиального по
, реализуемые однородной последовательностью квантовых схем полиномиального по  размера, чтобы функция
размера, чтобы функция 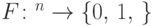 принадлежала классу BQNP:
принадлежала классу BQNP:
Какому условию должно удовлетворять 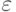 в неравенстве
в неравенстве  , если
, если 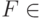
Каждое слагаемое локального гамильтониана ![H=\sum_{j}^{} H_j[S_j]](https://intuit.ru//sites/default/files/tex_cache/60401dd219ac693e3a7cf0806b6f48ee.png) является:
является:
Какому классу принадлежит локальный гамильтониан:
Из каких слагаемых состоит гамильтониан, сопоставляемый схеме, действующие на пространстве 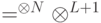 :
:
Какое слагаемое гамильтониана 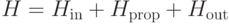 описывает эволюцию системы:
описывает эволюцию системы:
Утверждение о том, что схема, на вход которой подан вектор  , дает ответ 1 с вероятностью не меньше, чем
, дает ответ 1 с вероятностью не меньше, чем 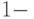 описывается формулой:
описывается формулой:
Кодовое расстояние - это:
Код исправляет  ошибок:
ошибок:
Пусть  - разложение пространства
- разложение пространства  в прямую сумму взаимно ортогональных подпространств. Тогда для любой пары матриц плотности
в прямую сумму взаимно ортогональных подпространств. Тогда для любой пары матриц плотности  ,
, 
Сколько будет базисных операторов для пространства 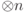 , образованного матрицами Паули?
, образованного матрицами Паули?
Симплектический квантовый код задается условиями:
Какими способами задаются торические коды?
Выберете верные утверждения:
Что из ниже перечисленного называется классической ошибкой?
Если есть пространство состояний  , причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств:
, причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств:  , тогда измеряющим будет называться всяки оператор вида:
, тогда измеряющим будет называться всяки оператор вида:
Чему эквивалентно условие
Сколько ошибок исправляет торический код?
Укажите верные утверждения:
Если на совместное состояние системы и прибора 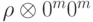 подействовать измеряющим оператором
подействовать измеряющим оператором  , то получим состояние:
, то получим состояние:
Как определяется слагаемое гамильтониана 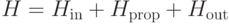 , отвечающее начальному состоянию:
, отвечающее начальному состоянию:
Множество состояний управляющего устройства в наборе 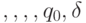 для задания машины Тьюринга - это:
для задания машины Тьюринга - это:
Если имеется действие  , то :
, то :
Предикат, задающий 3-КНФ:
Какая цепочка эквивалентностей является некорректной:
Выберите неверное утверждение:
Выберите неверное утверждение:
В качестве первого сомножителя пространства 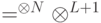 , на котором действует гамильтониан, сопоставляемый схеме, выступает:
, на котором действует гамильтониан, сопоставляемый схеме, выступает:
Преобразование матриц плотности  где
где  , называется:
, называется:
Специальная ортогональная группа на трехмерном евклидовом пространстве обозначается записью:
Что послужило источником интереса к обратимым вычислениям:
Укажите верное утверждение:
Если существует квантовый алгоритм вычисления функции  , работающий за время
, работающий за время 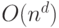 для некоторой константы
для некоторой константы  , то функция
, то функция 
Пространство состояний квантовой системы:
Последовательность кодов называется кодами с локальными проверками, если выполнены следующие условия:
Записи пространства состояний системы из  q-битов
q-битов 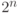 соответствует:
соответствует:
Какая пара операторов будет соответствовать соотношению 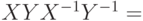 ?
?
Условие 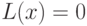 для предиката
для предиката  , принадлежащего классу
, принадлежащего классу 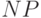 , означает, что:
, означает, что:
Формулировкой китайской теоремы об остатках является:
Если вероятность правильного ответа для каждого экземпляра из  запущенных машин Тьюринга равна
запущенных машин Тьюринга равна 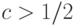 , то вероятность правильного ответа после голосования
, то вероятность правильного ответа после голосования  машин:
машин:
Физически реализуемым является преобразование вида:
Выберите неверное утверждение:
Выберите верное утверждение:
Что из ниже перечисленного называется фазовой ошибкой?
Каким преобразованием задается отбрасывание второй системы, если есть  :
:
Какая из ниже перечисленных формул является верной:
Что из ниже перечисленного верно отражает свойство "множество содержит много элементов":
Выберите верное утверждение:
В наборе 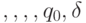 для задания машины Тьюринга множество S является:
для задания машины Тьюринга множество S является:
Время работы машины Тьюринга определяется:
Полный стандартный базис образуют булевы функции:
Выберите верное утверждение:
Выберите верное утверждение:
Предикат  принадлежит классу
принадлежит классу 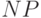 , если он представим в форме:
, если он представим в форме:
Сводимость по Карпу предиката 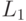 к предикату
к предикату 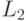 обозначается:
обозначается:
Теорема Кука, Левина утверждает, что:
Справедливым является утверждение:
Условие существования вероятностной машины Тьюринга  и полинома
и полинома 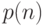 , причем машина
, причем машина  заведомо остановится за время, не превосходящее
заведомо остановится за время, не превосходящее 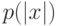 , определяет, что:
, определяет, что:
В соответствии с алгоритмом Евклида, если делить большее число на меньшее, то длина записи меньшего числа уменьшается на константу:
Вероятность получения ответа " - составное" для алгоритма проверки простоты составного числа n равна:
- составное" для алгоритма проверки простоты составного числа n равна:
Выберите верное утверждение:
Какое обозначает запись 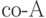 по отношению к классу А:
по отношению к классу А:
Утверждение о том, что для случайных независимых 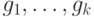 вероятность события
вероятность события 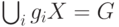 больше 0, содержится в записи :
больше 0, содержится в записи :
Какому классу принадлежит  , если существует такая игра с полиномиальным от длины входного слова числом ходов и полиномиально вычислимым результатом, что
, если существует такая игра с полиномиальным от длины входного слова числом ходов и полиномиально вычислимым результатом, что 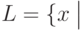 Б имеет выигрышную стратегию
Б имеет выигрышную стратегию  (Б - игрок, имеющих имя "белые"):
(Б - игрок, имеющих имя "белые"):
За какое количество тактов машина Тьюринга с оракулом проверяет, принадлежит ли записанное на оракульной ленте слово языку  :
:
Выберите верные тождества, где  - язык,
- язык, 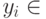 :
:
Множество состояний 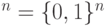 классической системы:
классической системы:
Что из перечисленного является характерным для квантового компьютера:
Обозначением вектора  является:
является:
Левая половина скалярного вектора 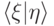 называется:
называется:
Какой вид имеет оператор, реализуемый квантовой схемой:
Перестановок на каком количестве бит является достаточным для реализации функции, заданной булевой схемой в полном базисе:
Из каких функций состоит базис  :
:
Какие из ниже перечисленных формул являются верными:
Если 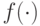 вычислима булевой схемой размера
вычислима булевой схемой размера  , то размер памяти, на которой можно вычислить функцию
, то размер памяти, на которой можно вычислить функцию 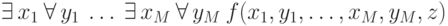 , равен:
, равен:
Условие приближенной реализуемости:
Выберите верное утверждение
Запись  имеет следующий смысл:
имеет следующий смысл:
Если имеется чистое состояние  , то разложение Шмидта имеет вид (
, то разложение Шмидта имеет вид (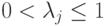 ,
, 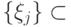 и
и 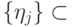 - ортонормированные вектора):
- ортонормированные вектора):
В формуле  , которой должна удовлетворять квантовая схема
, которой должна удовлетворять квантовая схема  , вычисляющая
, вычисляющая  , значение
, значение  :
:
Сколько экземпляров квантовой схемы 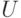 необходимо взять, чтобы уменьшить вероятность неудачи в
необходимо взять, чтобы уменьшить вероятность неудачи в  раз:
раз:
Выберите неверное утверждение
Формулы  достаточно для определения:
достаточно для определения:
Какая из ниже перечисленных формул является определением квантовой вероятности:
Частичный след от оператора  по пространству
по пространству  имеет вид:
имеет вид:
Если на пространстве 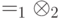 задана матрица плотности вида
задана матрица плотности вида  и имеется два подпространства
и имеется два подпространства 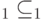 ,
,  , то справедливо равентство:
, то справедливо равентство:
Матрицу плотности чистого состояния 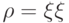 в матрицу
в матрицу  переводит:
переводит:
Выберите неверное утверждение:
Выберите верное утверждение:
Выберите верное утверждение:
Какой вид имеет линейный оператор?
Определите вид оператора  , действующего на пространстве
, действующего на пространстве
Как называется следующая формула: 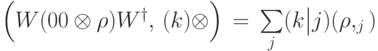 ?
?
Решение универсальной переборной задачи алгоритмом Гровера -
Какова вероятность получить делитель числа  в результате работы процедуры нахождения делителя (
в результате работы процедуры нахождения делителя ( - число различных простых делителей
- число различных простых делителей  ):
):
Условные вероятности для оператора ![\prod\limits_{r=1}^s \Xi(U_a)[r,A]](https://intuit.ru//sites/default/files/tex_cache/58682576919d4b606ee3f6e0c44dddf5.png) определяются, как (
определяются, как (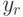 - значение в
- значение в  -ом бите):
-ом бите):
Равномерное распределение на множестве всех собственных чисел можно получить, если взять в качестве начального состояние, задаваемое следующей диагональной матрицей плотности:
Выберите верное утверждение:
В соответствии со свойствами квантовой механики формула 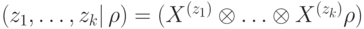 равна:
равна:
Выберите верное утверждение:
Чему равна левая часть формулы 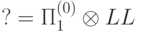
Если  ,
, 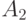 - неотрицательные операторы,
- неотрицательные операторы,  ,
, 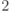 - их нулевые подпространства, причем
- их нулевые подпространства, причем 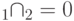 , ненулевые собственные числа
, ненулевые собственные числа  и
и 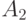 не меньше
не меньше 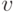 , где
, где 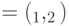 - угол между
- угол между  и
и 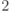 , то справедливым является равенство:
, то справедливым является равенство:
Как накапливаются ошибки при квантовом вычислении?
Следовая норма оператора  равна:
равна:
В чем заключается отличие симплектического кода от классических линейных кодов?
Выберете верные утверждения:
Оператор, переводящий  в
в 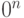 :
:
Если  - множество троек вида
- множество троек вида  описанием схемы - приближенная реализация в стандартном базисе, а
описанием схемы - приближенная реализация в стандартном базисе, а  (
(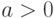 ,
,  - размер описания схемы). Тогда для
- размер описания схемы). Тогда для 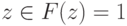 выполняется:
выполняется:
Выберите верное свойство скалярного произведения в гильбертовом пространстве:
Выберете верные утверждения:
Какой функцией является перестановка на двух битах 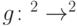 :
:
Выберите верное утверждение:
Если имеется последовательность булевых функций 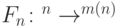 , то однородная последовательность схем, вычисляющих
, то однородная последовательность схем, вычисляющих 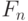 - это:
- это:
Действие унитарного оператора на произвольные матрицы плотности задается формулой:
Машина Тьюринга, переходящая в состояние, определяемое результатом некоторого случайного процесса, называется:
Отличием недетерминированной машины Тьюринга является:
В каком случае заведомо не существует псевдослучайных генераторов:
Порядок числа  в мультипликативной группе вычетов
в мультипликативной группе вычетов 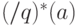 обозначается как:
обозначается как:
Сколько раз для нахождения факторизации числа необходимо применить подпрограмму, которая по любому составному числу вычисляет какой-то его делитель с вероятностью, не меньшей 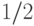 :
:
По какому правилу в квантовой постановке действует оракул, задающий оператор 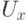 :
:
Каким образом будут распределены классические состояния квантовой системы, находящейся в состоянии 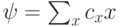 :
:
Выберите верное утверждение:
Условием остановки машины Тьюринга, находящейся в состоянии 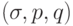 , является:
, является:
Важнейшими ресурсами, требующимися машине Тьюринга для вычислений, является:
Схема является формулой, если:
Строка таблицы вычисления  :
:
Справедливым является утверждение (запись):
Если установлена принадлежность предиката  к классу BPP, существуют полином
к классу BPP, существуют полином 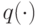 и предикат
и предикат 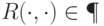 , то выражение
, то выражение 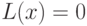 означает, что:
означает, что:
Из утверждения "вероятность того, что объекта с нужными свойствами не существует, меньше 1" следует, что:
Использование генераторов псевдослучайных чисел является основой идеи:
В качестве 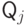 в булевой формуле
в булевой формуле  задаваемой задачей
задаваемой задачей 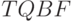 , где
, где 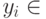 ,
, - некоторая логическая формула, выступает:
- некоторая логическая формула, выступает:
Какой вид имеет элемент Тоффоли:
Выберите верное утверждение:
Возможность точной реализации оператора квантовой схемой связана с использованием:
Каким условиям должна удовлетворять норма  на пространстве операторов:
на пространстве операторов:
Какое условие должно выполняться, чтобы схема  вычисляла
вычисляла  :
:
Выберите верное утверждение:
Полная длина квантовой схемы Z, размера L и точности не должна превышать:
В контексте классической вероятности распределение вероятностей задается:
Каким условиям эквивалентна физическая реализуемость линейного оператора  , записанного в координатном виде
, записанного в координатном виде 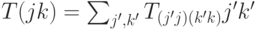 ?
?
В случае одного q-бита обнуление внедиагональных элементов можно получить, если применить оператор 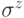 с вероятностью:
с вероятностью:
Как называется оператор вида 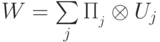 , если в пространстве состояний
, если в пространстве состояний  , причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств:
, причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств:  ?
?
Если применить измеряющий оператор к состоянию  , где
, где  , то вероятность наблюдения состояния
, то вероятность наблюдения состояния  можно записать в виде:
можно записать в виде:
Какому классу принадлежит функция 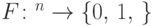 , если существует однородная последовательность квантовых схем полиномиального по
, если существует однородная последовательность квантовых схем полиномиального по  размера, реализующих такие операторы
размера, реализующих такие операторы 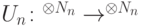 , что
, что 
Какому условию должно удовлетворять 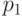 в неравенстве
в неравенстве  , если
, если 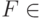
Если  - множество троек вида
- множество троек вида  , где
, где 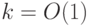 ,
, 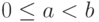 ,
, 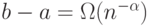 , (
, (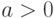 ), то для
), то для 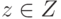 выполняются условия:
выполняются условия:
Как выглядят коммутационные соотношения между матрицами Паули?
Как называются векторы из кодового подпространства являющиеся собственными и обладающие наименьшей энергией?
Как называются коэффициенты 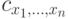 разложения вектора
разложения вектора 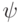 по базису
по базису 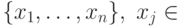 :
:
Автором каких квантовых алгоритмов является П. Шор:
Последовательность перестановок ![U_1[A_1],\dots, U_l[A_l]](https://intuit.ru//sites/default/files/tex_cache/83f6be2593a816115df273c5dce4beff.png) , где
, где 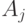 - множества битов,
- множества битов,  ,
,  - некоторое множество перестановок вида
- некоторое множество перестановок вида 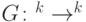 является:
является:
Какая запись является верной:
Какой размер имеет схема, которой в полном базисе реализуется функция 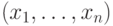 :
:
Можно ли в операторе  разложить
разложить  в сумму проекторов на собственные подпространства следующим образом:
в сумму проекторов на собственные подпространства следующим образом: 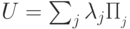 ,
,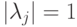 ?
?
В играх Артура - Мерлина в качестве Артура выступает:
Какой из операторов можно считать аналогом полупрозрачного зеркала?
Запись 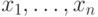 , где
, где 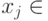 обозначает:
обозначает:
Если распределение вероятностей имеет вид 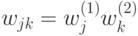 , имеется совместное распределение на множестве
, имеется совместное распределение на множестве 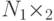 и событие не зависит от исхода во втором множестве
и событие не зависит от исхода во втором множестве 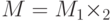 , то вероятность такого события выражается как:
, то вероятность такого события выражается как:
Для формы 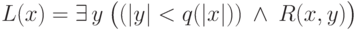 справедливо:
справедливо:
Выберите верное утверждение:
Какой вид имеет измеряющий оператор?
Для существующей недетерминированной машины Тьюринга, полинома 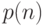 и предиката L условие
и предиката L условие 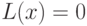 означает:
означает:
Условием полиномиальной сводимости предиката 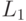 к предикату
к предикату 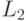 является:
является:
Выберите верное утверждение:
При двойном проведении алгоритма проверки простоты числа вероятность ошибки оказывается:
Выберите верное утверждение:
Унитарный оператор, сопоставляемый перестановке 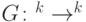 , имеет вид:
, имеет вид:
Решение проблемы выбора базиса в квантовых схемах связано с:
Чему соответствуют физическое состояние в квантовой механике:
Выберите верное утверждение:
Выберите верное утверждение:
Что будет являться произведением измеряющих операторов?
Если 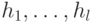 - независимые случайные равномерно распределенные элементы абелевой группы
- независимые случайные равномерно распределенные элементы абелевой группы  , то вероятность, с которой они порождают всю группу
, то вероятность, с которой они порождают всю группу  , определяется:
, определяется:
Класс, входящий в иерархию классов, определяемых играми Артура - Мерлина, обозначается как:
В контексте квантовой постановки нерешаемость задачи для любого предиката 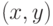 на квантовой схеме, означает, что:
на квантовой схеме, означает, что:
Чему равна суммарная длина  и
и  в формуле
в формуле  , которой должна удовлетворять квантовая схема
, которой должна удовлетворять квантовая схема  , вычисляющая
, вычисляющая  :
:
Выберите верное утверждение:
Что из перечисленного является характерным для тензорного произведения двух пространств  и
и 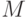 , в которых фиксированы базисы
, в которых фиксированы базисы 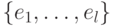 и
и 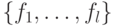
Выберите верное утверждение:
Какая из ниже перечисленных формул является верной:
Если подпространство  ортогонально подпространству
ортогонально подпространству 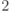 , то для любой матрицы плотности
, то для любой матрицы плотности  выполняется равенство:
выполняется равенство:
Однозначно определенная совокупность инструкций по преобразованию исходных данных в результат - это:
Функция  является функцией полиномиального роста, если для некоторой константы
является функцией полиномиального роста, если для некоторой константы  при достаточно больших
при достаточно больших  выполняется неравенство:
выполняется неравенство:
Предикатом 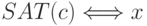 задается:
задается:
Возможность действовать на бесконечном множестве описывается:
Классическим объектом, соответствующим унитарному оператору является:
Если  и
и 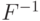 вычислимы булевыми схемами размеров
вычислимы булевыми схемами размеров 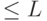 , то
, то  реализуется обратимой схемой размера:
реализуется обратимой схемой размера:
Каково действие унитарного оператора  в трехмерном евклидовом пространстве:
в трехмерном евклидовом пространстве:
Наибольшее собственное число оператора 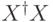 определяется как:
определяется как:
Обозначение оператора, реализуемого универсальной квантовой схемой, имеет вид:
Какая из ниже перечисленных формул для квантовой вероятности является верной:
Укажите верное утверждение:
Зная, что ![\Prob\left[\left|\frac{\sum\nolimits_{r=1}^{s}y_r}{s}-\PP(1\big|k)\right| >\delta\right]<2e^{-c\delta^{2}s}](https://intuit.ru//sites/default/files/tex_cache/9009c53c494d327bbbeb05931b097821.png) , где
, где  - константа, за сколько испытаний можно добиться вероятности ошибки
- константа, за сколько испытаний можно добиться вероятности ошибки 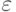 при фиксированном
при фиксированном 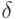 :
:
Какого типа код Хэмминга 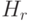 ?
?
В задаче о скрытой подгруппе в  имеется "скрытая подгруппа"
имеется "скрытая подгруппа"  , порядок которой
, порядок которой 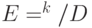 не превосходит:
не превосходит:
За какое количество шагов классический компьютер вычислит значение предиката  (
( - количество битов в записи y):
- количество битов в записи y):
Сколько кодовых q-битов используют коды со сколь угодно большим кодовым расстоянием?
Состояние перехода вероятностной машины Тьюринга определяется:
Условием алгоритма проверки простоты числа  , определяющим что
, определяющим что  - составное, где
- составное, где  - случайное среди чисел от 1 до
- случайное среди чисел от 1 до  ,
, 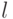 - нечетное, является:
- нечетное, является:
Количество состояний системы, где 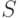 - память,
- память, 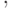 - соответственно множество состояний управляющего устройства и алфавит рассматриваемой машины Тьюринга, определяется по формуле:
- соответственно множество состояний управляющего устройства и алфавит рассматриваемой машины Тьюринга, определяется по формуле:
Выражение 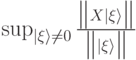 определяет:
определяет:
Какой полиномиальный размер имеет булева функция для умножения вычетов:
Чему равно кодовое расстояние для симплектического кода  ?
?
Как получить условные вероятности для произведения измеряющих "разными приборами" операторов?
Алгоритм Евклида основан на рекурсивном использовании равенства:
Чему равна вероятность того, что случайный сдвиг  не покрывает (не содержит) некоторый фиксированный элемент, где
не покрывает (не содержит) некоторый фиксированный элемент, где  - некоторая группа, а
- некоторая группа, а  - подмножество
- подмножество  :
:
Какому размеру должны удовлетворять булевы схемы, вычисляющие  и
и 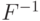 , чтобы
, чтобы  реализовалась обратимой схемой размера
реализовалась обратимой схемой размера 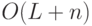 :
:
Коэффициенты разложения по выделенному базису классических состояний называются:
Если имеется  , а
, а  , то детерминированное измерение будет иметь вид:
, то детерминированное измерение будет иметь вид:
При сравнении вероятностных распределений в 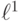 - норме,если
- норме,если 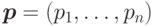 ,
,  - два распределения, то мерой их различия считаем
- два распределения, то мерой их различия считаем
Для любого классического вероятностного алгоритма, делающего не более  обращений к оракулу (
обращений к оракулу ( ), существует подгруппа
), существует подгруппа  и соответствующая функция
и соответствующая функция  , для которой вероятность ошибки алгоритма:
, для которой вероятность ошибки алгоритма:
Выберите верное утверждение:
Для доказательства физической реализации преобразования вида 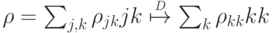 на завершающем шаге необходимым является:
на завершающем шаге необходимым является:
При доказательстве утверждения "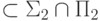 " используется:
" используется:
По какой причине копирование произвольного квантового состояния 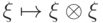 физически нереализуемо:
физически нереализуемо:
Какая из ниже перечисленных формул является верной:
Вероятность обнаружить систему в конкретном базисном состоянии определяется, как:

 для квантового состояния, задаваемого матрицей плотности
для квантового состояния, задаваемого матрицей плотности  и подпространства
и подпространства  :
: случайных сдвигов не покрывают фиксированный элемент, где
случайных сдвигов не покрывают фиксированный элемент, где  - некоторая группа, а
- некоторая группа, а  - подмножество
- подмножество  :
: принадлежит классу NP, если есть частично определенная функция
принадлежит классу NP, если есть частично определенная функция  от двух переменных, такая что:
от двух переменных, такая что: - разложение числа на взаимно простые множители, то существует взаимно однозначное соответствие между остатками от деления на
- разложение числа на взаимно простые множители, то существует взаимно однозначное соответствие между остатками от деления на  и парами остатков от деления на
и парами остатков от деления на  и на
и на 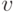 " - утверждает:
" - утверждает: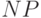 -полный предикат можно вычислить за время
-полный предикат можно вычислить за время 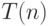 , то любой предикат из
, то любой предикат из 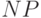 для некоторого числа
для некоторого числа  можно вычислить за время:
можно вычислить за время: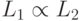 ,
, 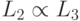 , то
, то 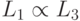 является достаточным доказательством утверждения:
является достаточным доказательством утверждения:![W=U_l[A_l]\cdot\ldots\cdot U_1[A_1]](https://intuit.ru//sites/default/files/tex_cache/526cd679d7bedf77b6a7aab913526691.png) в расширенном смысле:
в расширенном смысле: , то реализовать его можно обратимым способом с использованием памяти:
, то реализовать его можно обратимым способом с использованием памяти: действует на трехмерном евклидовом пространстве (
действует на трехмерном евклидовом пространстве ( ), то задаваемый изоморфизм имеет вид:
), то задаваемый изоморфизм имеет вид: действует на трехмерном евклидовом пространстве (
действует на трехмерном евклидовом пространстве ( ), для матриц Паули
), для матриц Паули  ,
,  соответствует повороту вокруг оси X на:
соответствует повороту вокруг оси X на: q-битов находится в состоянии
q-битов находится в состоянии 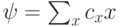 , то вероятность обнаружить систему в состоянии x определяется как:
, то вероятность обнаружить систему в состоянии x определяется как: в пространство большей размерности, задаваемое формулой
в пространство большей размерности, задаваемое формулой  , матрица плотности
, матрица плотности  преобразуется:
преобразуется: являлся физически реализуемым преобразованием матриц плотности:
являлся физически реализуемым преобразованием матриц плотности: , причем для любого чистого состояния
, причем для любого чистого состояния  выполняется свойство:
выполняется свойство: 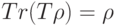 , то для любого оператора
, то для любого оператора  справедливым является равенство (
справедливым является равенство ( - некоторая фиксированная матрица плотности на пространстве
- некоторая фиксированная матрица плотности на пространстве  ):
): в
в  ,
,  - квантовая часть и
- квантовая часть и  - классическая часть системы, результат является диагональным по отношению:
- классическая часть системы, результат является диагональным по отношению: , причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств:
, причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств:  , тогда всякий оператор вида
, тогда всякий оператор вида 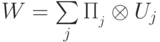 будет называться:
будет называться: , подсоединить прибор с выделенным базисом, то совместное состояние системы и прибора будет описываться матрицей плотности вида:
, подсоединить прибор с выделенным базисом, то совместное состояние системы и прибора будет описываться матрицей плотности вида: в операторе
в операторе  можно разложить в сумму проекторов на собственные подпространства следующим образом:
можно разложить в сумму проекторов на собственные подпространства следующим образом: 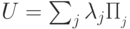 ,
,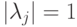 ?
? разложить в сумму проекторов на собственные подпространства следующим образом:
разложить в сумму проекторов на собственные подпространства следующим образом: 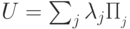 ,
,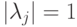 , то
, то 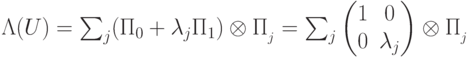 . В этом случае условные вероятности будут равны:
. В этом случае условные вероятности будут равны: , где
, где  , то вероятность наблюдения состояния
, то вероятность наблюдения состояния  можно записать в виде:
можно записать в виде: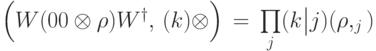 ?
?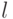 дробей вида
дробей вида  то вероятность того, что наименьшее общее кратное их знаменателей отлично от
то вероятность того, что наименьшее общее кратное их знаменателей отлично от  (равномерно распределенное на множестве
(равномерно распределенное на множестве  случайное число):
случайное число): обращений к оракулу и каждый вопрос имеет длину
обращений к оракулу и каждый вопрос имеет длину  , то размер квантовой схемы определяется как:
, то размер квантовой схемы определяется как: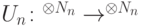 , реализуемые однородной последовательностью квантовых схем полиномиального по
, реализуемые однородной последовательностью квантовых схем полиномиального по  размера, чтобы функция
размера, чтобы функция 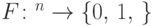 принадлежала классу BQNP:
принадлежала классу BQNP: , дает ответ 1 с вероятностью не меньше, чем
, дает ответ 1 с вероятностью не меньше, чем 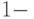 описывается формулой:
описывается формулой: - разложение пространства
- разложение пространства  в прямую сумму взаимно ортогональных подпространств. Тогда для любой пары матриц плотности
в прямую сумму взаимно ортогональных подпространств. Тогда для любой пары матриц плотности  ,
, 
 , причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств:
, причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств:  , тогда измеряющим будет называться всяки оператор вида:
, тогда измеряющим будет называться всяки оператор вида: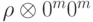 подействовать измеряющим оператором
подействовать измеряющим оператором  , то получим состояние:
, то получим состояние: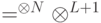 , на котором действует гамильтониан, сопоставляемый схеме, выступает:
, на котором действует гамильтониан, сопоставляемый схеме, выступает: , работающий за время
, работающий за время 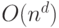 для некоторой константы
для некоторой константы  , то функция
, то функция 
 запущенных машин Тьюринга равна
запущенных машин Тьюринга равна 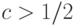 , то вероятность правильного ответа после голосования
, то вероятность правильного ответа после голосования  машин:
машин: и полинома
и полинома 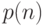 , причем машина
, причем машина  заведомо остановится за время, не превосходящее
заведомо остановится за время, не превосходящее 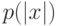 , определяет, что:
, определяет, что: - составное" для алгоритма проверки простоты составного числа n равна:
- составное" для алгоритма проверки простоты составного числа n равна: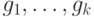 вероятность события
вероятность события 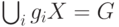 больше 0, содержится в записи :
больше 0, содержится в записи : , если существует такая игра с полиномиальным от длины входного слова числом ходов и полиномиально вычислимым результатом, что
, если существует такая игра с полиномиальным от длины входного слова числом ходов и полиномиально вычислимым результатом, что 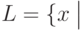 Б имеет выигрышную стратегию
Б имеет выигрышную стратегию  (Б - игрок, имеющих имя "белые"):
(Б - игрок, имеющих имя "белые"): :
: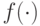 вычислима булевой схемой размера
вычислима булевой схемой размера  , то размер памяти, на которой можно вычислить функцию
, то размер памяти, на которой можно вычислить функцию 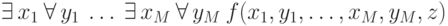 , равен:
, равен: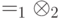 задана матрица плотности вида
задана матрица плотности вида  и имеется два подпространства
и имеется два подпространства 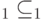 ,
,  , то справедливо равентство:
, то справедливо равентство: в результате работы процедуры нахождения делителя (
в результате работы процедуры нахождения делителя ( - число различных простых делителей
- число различных простых делителей  ):
): ,
, 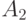 - неотрицательные операторы,
- неотрицательные операторы,  ,
, 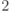 - их нулевые подпространства, причем
- их нулевые подпространства, причем 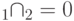 , ненулевые собственные числа
, ненулевые собственные числа  и
и 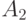 не меньше
не меньше 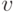 , где
, где 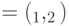 - угол между
- угол между  и
и 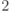 , то справедливым является равенство:
, то справедливым является равенство: - множество троек вида
- множество троек вида  описанием схемы - приближенная реализация в стандартном базисе, а
описанием схемы - приближенная реализация в стандартном базисе, а  (
(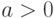 ,
,  - размер описания схемы). Тогда для
- размер описания схемы). Тогда для 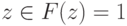 выполняется:
выполняется: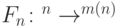 , то однородная последовательность схем, вычисляющих
, то однородная последовательность схем, вычисляющих 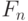 - это:
- это: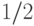 :
: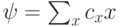 :
: к классу BPP, существуют полином
к классу BPP, существуют полином 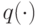 и предикат
и предикат 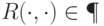 , то выражение
, то выражение 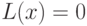 означает, что:
означает, что: , записанного в координатном виде
, записанного в координатном виде 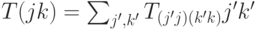 ?
?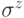 с вероятностью:
с вероятностью: 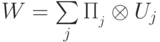 , если в пространстве состояний
, если в пространстве состояний  , причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств:
, причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств:  ?
? , где
, где  , то вероятность наблюдения состояния
, то вероятность наблюдения состояния  можно записать в виде:
можно записать в виде: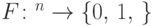 , если существует однородная последовательность квантовых схем полиномиального по
, если существует однородная последовательность квантовых схем полиномиального по  размера, реализующих такие операторы
размера, реализующих такие операторы 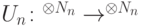 , что
, что 
![U_1[A_1],\dots, U_l[A_l]](https://intuit.ru//sites/default/files/tex_cache/83f6be2593a816115df273c5dce4beff.png) , где
, где 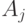 - множества битов,
- множества битов,  ,
,  - некоторое множество перестановок вида
- некоторое множество перестановок вида 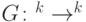 является:
является: разложить
разложить  в сумму проекторов на собственные подпространства следующим образом:
в сумму проекторов на собственные подпространства следующим образом: 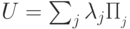 ,
,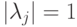 ?
?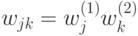 , имеется совместное распределение на множестве
, имеется совместное распределение на множестве 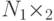 и событие не зависит от исхода во втором множестве
и событие не зависит от исхода во втором множестве 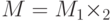 , то вероятность такого события выражается как:
, то вероятность такого события выражается как: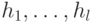 - независимые случайные равномерно распределенные элементы абелевой группы
- независимые случайные равномерно распределенные элементы абелевой группы  , то вероятность, с которой они порождают всю группу
, то вероятность, с которой они порождают всю группу  , определяется:
, определяется: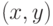 на квантовой схеме, означает, что:
на квантовой схеме, означает, что: и
и  в формуле
в формуле  , которой должна удовлетворять квантовая схема
, которой должна удовлетворять квантовая схема  , вычисляющая
, вычисляющая  :
: и
и 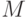 , в которых фиксированы базисы
, в которых фиксированы базисы 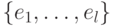 и
и 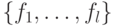
 ортогонально подпространству
ортогонально подпространству 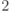 , то для любой матрицы плотности
, то для любой матрицы плотности  выполняется равенство:
выполняется равенство: является функцией полиномиального роста, если для некоторой константы
является функцией полиномиального роста, если для некоторой константы  при достаточно больших
при достаточно больших  выполняется неравенство:
выполняется неравенство:![\Prob\left[\left|\frac{\sum\nolimits_{r=1}^{s}y_r}{s}-\PP(1\big|k)\right| >\delta\right]<2e^{-c\delta^{2}s}](https://intuit.ru//sites/default/files/tex_cache/9009c53c494d327bbbeb05931b097821.png) , где
, где  - константа, за сколько испытаний можно добиться вероятности ошибки
- константа, за сколько испытаний можно добиться вероятности ошибки 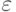 при фиксированном
при фиксированном 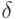 :
: (
( - количество битов в записи y):
- количество битов в записи y): , определяющим что
, определяющим что  - составное, где
- составное, где  - случайное среди чисел от 1 до
- случайное среди чисел от 1 до  ,
, 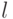 - нечетное, является:
- нечетное, является: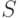 - память,
- память, 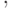 - соответственно множество состояний управляющего устройства и алфавит рассматриваемой машины Тьюринга, определяется по формуле:
- соответственно множество состояний управляющего устройства и алфавит рассматриваемой машины Тьюринга, определяется по формуле: не покрывает (не содержит) некоторый фиксированный элемент, где
не покрывает (не содержит) некоторый фиксированный элемент, где  - некоторая группа, а
- некоторая группа, а  - подмножество
- подмножество  :
: и
и 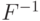 , чтобы
, чтобы  реализовалась обратимой схемой размера
реализовалась обратимой схемой размера 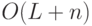 :
: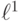 - норме,если
- норме,если 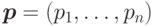 ,
,  - два распределения, то мерой их различия считаем
- два распределения, то мерой их различия считаем обращений к оракулу (
обращений к оракулу ( ), существует подгруппа
), существует подгруппа  и соответствующая функция
и соответствующая функция  , для которой вероятность ошибки алгоритма:
, для которой вероятность ошибки алгоритма: на завершающем шаге необходимым является:
на завершающем шаге необходимым является: