Элементарному преобразованию в квантовом случае соответствует определение:
(Отметьте один правильный вариант ответа.)
Варианты ответа
тензорное произведение произвольного унитарного оператора, действующего на части сомножителей 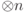 , где
, где  мало (
мало (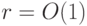 ), и тождественного оператора, действующего на остальных сомножителях(Верный ответ)
), и тождественного оператора, действующего на остальных сомножителях(Верный ответ)
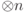 , где
, где  мало (
мало (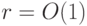 ), и тождественного оператора, действующего на остальных сомножителях(Верный ответ)
), и тождественного оператора, действующего на остальных сомножителях(Верный ответ)
функция из  в
в 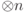 , которая зависит от небольшого числа битов и изменяет также небольшое число битов
, которая зависит от небольшого числа битов и изменяет также небольшое число битов
 в
в 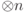 , которая зависит от небольшого числа битов и изменяет также небольшое число битов
, которая зависит от небольшого числа битов и изменяет также небольшое число битов
функция из  в
в  , которая зависит от небольшого числа битов и изменяет также небольшое число битов
, которая зависит от небольшого числа битов и изменяет также небольшое число битов
 в
в  , которая зависит от небольшого числа битов и изменяет также небольшое число битов
, которая зависит от небольшого числа битов и изменяет также небольшое число битов

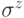 с вероятностью:
с вероятностью:  q-битов
q-битов 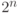 соответствует:
соответствует: и
и 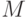 , в которых фиксированы базисы
, в которых фиксированы базисы 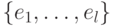 и
и 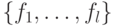 :
: в пространство большей размерности, задаваемое формулой
в пространство большей размерности, задаваемое формулой  , матрица плотности
, матрица плотности  преобразуется:
преобразуется: действует на трехмерном евклидовом пространстве (
действует на трехмерном евклидовом пространстве ( ), для матриц Паули
), для матриц Паули  ,
,  соответствует повороту вокруг оси
соответствует повороту вокруг оси  разложить в сумму проекторов на собственные подпространства следующим образом:
разложить в сумму проекторов на собственные подпространства следующим образом: 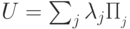 ,
,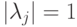 , то
, то 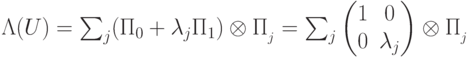 . В этом случае условные вероятности будут равны:
. В этом случае условные вероятности будут равны: