Классические и квантовые вычисления

<<- Назад к вопросам

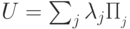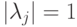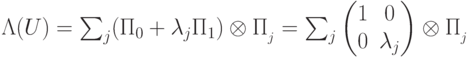Если унитарный оператор разложить в сумму проекторов на собственные подпространства следующим образом: $U=\sum_{j} \lambda_j\Pi_{\calL_j}$ , $|\lambda_j|=1$ , то $\Lambda(U)=\sum_{j} (\Pi_0+\lambda_j\Pi_1)\otimes\Pi_{\calL_j}= \sum_{j}^{} \begin{pmatrix} 1&0\\ 0&\lambda_j \end{pmatrix} \otimes\Pi_{\calL_j}$ . В этом случае условные вероятности будут равны:

(Отметьте один правильный вариант ответа.)

Варианты ответа

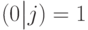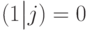$\PP(0\big|j) =1$ и $\PP(1\big|j) =0$ (Верный ответ)

нет верного ответа

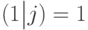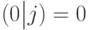
$\PP(1\big|j) =1$ и $\PP(0\big|j) =0$

Похожие вопросы

Почему

в операторе $\Lambda(U)=\Pi_0\otimes I + \Pi_1\otimes U$ можно разложить в сумму проекторов на собственные подпространства следующим образом: $U=\sum_{j} \lambda_j\Pi_{\calL_j}$ , $|\lambda_j|=1$ ?

Можно ли в операторе $\Lambda(U)=\Pi_0\otimes I + \Pi_1\otimes U$ разложить

в сумму проекторов на собственные подпространства следующим образом: $U=\sum_{j} \lambda_j\Pi_{\calL_j}$ , $|\lambda_j|=1$ ?

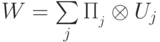Как называется оператор вида $W=\sum\limits_{j}^{} \Pi_{\calL_j}\otimes U_j$ , если в пространстве состояний $\calN\otimes\calK$ , причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств: $\calN\double=\bigoplus\limits_j \calL_j$ ?

Если есть пространство состояний $\calN\otimes\calK$ , причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств: $\calN\double=\bigoplus\limits_j \calL_j$ , тогда всякий оператор вида $W=\sum\limits_{j}^{} \Pi_{\calL_j}\otimes U_j$ будет называться:

Преобразование матриц плотности $\begin{equation}\rho\ \mapsto\ \sum_{j}^{}\PP(\rho,\calL_j)\left(\gamma^{(j)},j\right), \end{equation}$ где $\gamma^{(j)}=\PP(\rho,\calL_j)^{-1}\times\Pi_{\calL_j} \rho\Pi_{\calL_j}$ , называется:

Верно ли, что если применить измеряющий оператор к состоянию $\ket0\bra0\otimes\rho$ , где $\rho\double\in\LL(\calN)$ , то вероятность наблюдения состояния

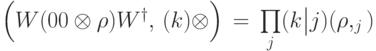можно записать в виде: $\PP\Bigl(W(\ket0\bra0\otimes\rho)W^\dagger,\,\CC(\ket{k})\otimes\calN\Bigr) \,=\, \prod\limits_{j} \PP(k\big| j) \PP(\rho, \calL_j)$ ?

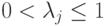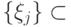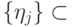Если имеется чистое состояние $\ket{\psi}\in\calN\otimes\calF$ , то разложение Шмидта имеет вид ( $0<\lambda_j\le 1$ , $\{\ket{\xi_j}\}\subset\calN$ и $\{\ket{\eta_j}\}\subset\calF$ - ортонормированные вектора):

Если есть пространство состояний $\calN\otimes\calK$ , причем первый сомножитель разложен в прямую сумму попарно ортогональных подпространств: $\calN\double=\bigoplus\limits_j \calL_j$ , тогда измеряющим будет называться всяки оператор вида:

Каким образом определяется частичный след оператора

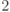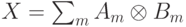по пространству $\calN_2$ ( $X=\sum_{m}^{} A_m\otimes B_m$ ):

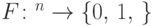Какому классу принадлежит функция $F\colon \cb^n\to \{0,\,1,\,\}$ , если существует однородная последовательность квантовых схем полиномиального по

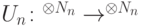размера, реализующих такие операторы $U_n\colon \BB^{\otimes N_n}\to \BB^{\otimes N_n}$ , что $F_n(x)=1 & \Longrightarrow & \exists\, \ket\xi\: \PP\Bigl(U_n\ket\xi\otimes\ket{x}\otimes\ket{0^{N_n-n-m_n}},\calM\Bigr) \geq p_1,\\ F_n(x)=0 & \Longrightarrow & \forall\, \ket\xi\: \PP\Bigl(U_n\ket\xi\otimes\ket{x}\otimes\ket{0^{N_n-n-m_n}},\calM\Bigr) \leq p_0.$

Классические и квантовые вычисления

Если унитарный оператор разложить в сумму проекторов на собственные подпространства следующим образом: ,, то . В этом случае условные вероятности будут равны: