Чему равна вероятность получения базисного состояния,  при измерении состояния
при измерении состояния  :
:
(Отметьте один правильный вариант ответа.)
Варианты ответа
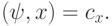
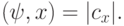
 (Верный ответ)
(Верный ответ)

 при измерении состояния
при измерении состояния  :
: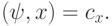
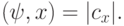
 (Верный ответ)
(Верный ответ)
 для квантового состояния, задаваемого матрицей плотности
для квантового состояния, задаваемого матрицей плотности  и подпространства
и подпространства  :
: , причем для любого чистого состояния
, причем для любого чистого состояния  выполняется свойство:
выполняется свойство: 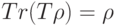 , то для любого оператора
, то для любого оператора  справедливым является равенство (
справедливым является равенство ( - некоторая фиксированная матрица плотности на пространстве
- некоторая фиксированная матрица плотности на пространстве  ):
): , где
, где  , то вероятность наблюдения состояния
, то вероятность наблюдения состояния  можно записать в виде:
можно записать в виде: и
и  в формуле
в формуле  , которой должна удовлетворять квантовая схема
, которой должна удовлетворять квантовая схема  , вычисляющая
, вычисляющая  :
: случайных сдвигов не покрывают фиксированный элемент, где
случайных сдвигов не покрывают фиксированный элемент, где  - некоторая группа, а
- некоторая группа, а  - подмножество
- подмножество  :
: , где
, где  , то вероятность наблюдения состояния
, то вероятность наблюдения состояния  можно записать в виде:
можно записать в виде: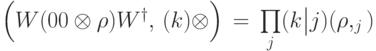 ?
? не покрывает (не содержит) некоторый фиксированный элемент, где
не покрывает (не содержит) некоторый фиксированный элемент, где  - некоторая группа, а
- некоторая группа, а  - подмножество
- подмножество  :
: ,
, 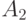 - неотрицательные операторы,
- неотрицательные операторы,  ,
, 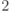 - их нулевые подпространства, причем
- их нулевые подпространства, причем 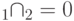 , ненулевые собственные числа
, ненулевые собственные числа  и
и 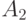 не меньше
не меньше 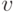 , где
, где 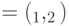 - угол между
- угол между  и
и  , то справедливым является равенство:
, то справедливым является равенство: