Каким условиям должны удовлетворять операторы 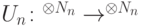 , реализуемые однородной последовательностью квантовых схем полиномиального по
, реализуемые однородной последовательностью квантовых схем полиномиального по  размера, чтобы функция
размера, чтобы функция 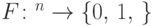 принадлежала классу BQNP:
принадлежала классу BQNP:
(Отметьте один правильный вариант ответа.)
Варианты ответа
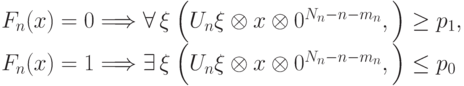

 (Верный ответ)
(Верный ответ)


 в пространство большей размерности, задаваемое формулой
в пространство большей размерности, задаваемое формулой  , матрица плотности
, матрица плотности  преобразуется:
преобразуется: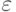 в неравенстве
в неравенстве 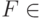
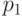 в неравенстве
в неравенстве  , работающий за время
, работающий за время 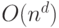 для некоторой константы
для некоторой константы  , то функция
, то функция  , где
, где  , то вероятность наблюдения состояния
, то вероятность наблюдения состояния  можно записать в виде:
можно записать в виде: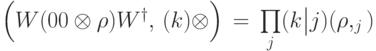 ?
? в операторе
в операторе  можно разложить в сумму проекторов на собственные подпространства следующим образом:
можно разложить в сумму проекторов на собственные подпространства следующим образом: 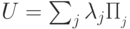 ,
,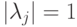 ?
? , причем для любого чистого состояния
, причем для любого чистого состояния 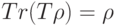 , то для любого оператора
, то для любого оператора  справедливым является равенство (
справедливым является равенство ( - некоторая фиксированная матрица плотности на пространстве
- некоторая фиксированная матрица плотности на пространстве  ):
):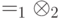 задана матрица плотности вида
задана матрица плотности вида  и имеется два подпространства
и имеется два подпространства 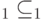 ,
,  , то справедливо равентство:
, то справедливо равентство: