Если на совместное состояние системы и прибора 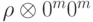 подействовать измеряющим оператором
подействовать измеряющим оператором  , то получим состояние:
, то получим состояние:
(Отметьте один правильный вариант ответа.)
Варианты ответа
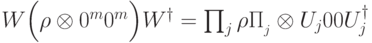
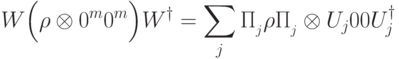 (Верный ответ)
(Верный ответ)
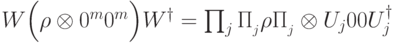

 , то разложение Шмидта имеет вид (
, то разложение Шмидта имеет вид (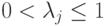 ,
, 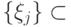 и
и 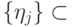 - ортонормированные вектора):
- ортонормированные вектора):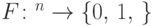 , если существует однородная последовательность квантовых схем полиномиального по
, если существует однородная последовательность квантовых схем полиномиального по  размера, реализующих такие операторы
размера, реализующих такие операторы 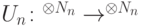 , что
, что 
 , где
, где  , то вероятность наблюдения состояния
, то вероятность наблюдения состояния  можно записать в виде:
можно записать в виде: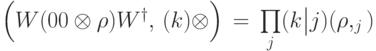 ?
? - множество троек вида
- множество троек вида  , где
, где 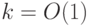 ,
, 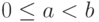 ,
, 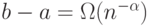 , (
, (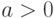 ), то для
), то для 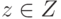 выполняются условия:
выполняются условия: , подсоединить прибор с выделенным базисом, то совместное состояние системы и прибора будет описываться матрицей плотности вида:
, подсоединить прибор с выделенным базисом, то совместное состояние системы и прибора будет описываться матрицей плотности вида: в операторе
в операторе  можно разложить в сумму проекторов на собственные подпространства следующим образом:
можно разложить в сумму проекторов на собственные подпространства следующим образом: 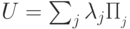 ,
,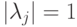 ?
?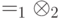 задана матрица плотности вида
задана матрица плотности вида  и имеется два подпространства
и имеется два подпространства 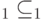 ,
,  , то справедливо равентство:
, то справедливо равентство: в пространство большей размерности, задаваемое формулой
в пространство большей размерности, задаваемое формулой  , матрица плотности
, матрица плотности  преобразуется:
преобразуется: ,
, 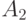 - неотрицательные операторы,
- неотрицательные операторы,  ,
, 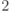 - их нулевые подпространства, причем
- их нулевые подпространства, причем 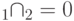 , ненулевые собственные числа
, ненулевые собственные числа 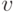 , где
, где 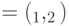 - угол между
- угол между