Производство двух видов продукции приносит прибыль в расчете на единицу, соответственно, 6; 5.
Для производства продукции используются ресурсы трех видов в следующих количествах (первое число относится к первому виду продукции, второе ко второму).
Первый ресурс: 1 и 6.
Второй ресурс 3 и 1
Третий ресурс 4 и 7.
Ресурсы имеются в количествах, соответственно: 54; 6 и 42.
Найти наибольшую прибыль.
С базы на склад в среднем раз в  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением 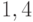 ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 4 | 5 | 1 | 2 | 110 |
| II | 7 | 1 | 8 | 6 | 40 |
| III | 6 | 3 | 3 | 7 | 70 |
| IV | 4 | 2 | 1 | 3 | 50 |
| Наличие | 90 | 40 | 50 | 90 | 270 |
Найти оптимальный план перевозок и определить его стоимость.
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 2 | 2 | 4 | 1 | 0 | 0 | 30 |
| 0 | 8 | 1 | 1 | 0 | 1 | 0 | 45 |
| 0 | 1 | 4 | 1 | 0 | 0 | 1 | 120 |
| 1 | -8 | -4 | -4 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 2 | 2 | 4 | 1 | 0 | 0 | 20 |
| 0 | 6 | 1 | 1 | 0 | 1 | 0 | 60 |
| 0 | 2 | 4 | 1 | 0 | 0 | 1 | 140 |
| 1 | -6 | -8 | -4 | 0 | 0 | 0 | 0 |
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 4 | 9 | 5 | 7 | 20 |
| II | 1 | 3 | 5 | 2 | 40 |
| III | 4 | 7 | 3 | 5 | 30 |
| IV | 6 | 4 | 3 | 5 | 20 |
| Наличие | 40 | 20 | 10 | 40 | 110 |
Создать исходный план перевозок методом северо-западного угла и определить его стоимость.
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 2 | 3 | 4 | 5 | 60 |
| II | 1 | 2 | 4 | 6 | 30 |
| III | 3 | 1 | 5 | 1 | 30 |
| IV | 4 | 1 | 2 | 4 | 30 |
| Наличие | 10 | 70 | 50 | 20 | 150 |
Создать исходный план перевозок методом северо-западного угла и определить его стоимость.
Производство двух видов продукции приносит прибыль в расчете на единицу, соответственно, 5; 4.
Для производства продукции используются ресурсы трех видов в следующих количествах (первое число относится к первому виду продукции, второе ко второму).
Первый ресурс: 1 и 6.
Второй ресурс 3 и 1
Третий ресурс 4 и 7.
Ресурсы имеются в количествах, соответственно: 54; 6 и 42.
Найти программу производства, приносящую наибольшую прибыль.
С базы на склад в среднем раз в 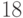 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в 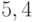 ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  день. Известно, что к началу первого дня остаток на складе составлял
день. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
С базы на склад в среднем раз в  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
С базы на склад в среднем раз в  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в 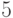 ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  день. Известно, что к началу первого дня остаток на складе составлял
день. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
С базы на склад в среднем раз в 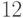 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в 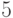 ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
С базы на склад в среднем раз в  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве 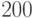 ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
С базы на склад в среднем раз в  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением 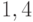 ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет 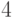 дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 8 | 6 | 4 | 6 | 110 |
| II | 2 | 7 | 2 | 3 | 40 |
| III | 5 | 7 | 8 | 3 | 70 |
| IV | 8 | 5 | 2 | 3 | 50 |
| Наличие | 90 | 40 | 50 | 90 | 270 |
Создать исходный план перевозок методом северо-западного угла и определить его стоимость.
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 3 | 7 | 4 | 6 | 100 |
| II | 2 | 4 | 3 | 3 | 40 |
| III | 3 | 5 | 6 | 3 | 60 |
| IV | 5 | 5 | 2 | 6 | 50 |
| Наличие | 80 | 40 | 40 | 90 | 250 |
Найти оптимальный план перевозок и определить его стоимость.
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 2 | 3 | 4 | 5 | 100 |
| II | 1 | 2 | 4 | 6 | 40 |
| III | 3 | 1 | 5 | 1 | 60 |
| IV | 4 | 1 | 2 | 4 | 50 |
| Наличие | 80 | 40 | 40 | 90 | 250 |
Создать исходный план перевозок методом северо-западного угла и определить его стоимость.
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 8 | 6 | 4 | 6 | 70 |
| II | 2 | 7 | 2 | 3 | 30 |
| III | 5 | 7 | 8 | 3 | 40 |
| IV | 8 | 5 | 2 | 3 | 60 |
| Наличие | 80 | 10 | 50 | 60 | 200 |
Найти оптимальный план перевозок и определить его стоимость.
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 4 | 8 | 6 | 7 | 20 |
| II | 1 | 3 | 6 | 2 | 40 |
| III | 4 | 7 | 6 | 5 | 30 |
| IV | 6 | 4 | 3 | 5 | 20 |
| Наличие | 40 | 20 | 10 | 40 | 110 |
Создать исходный план перевозок методом северо-западного угла и определить его стоимость.
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 4 | 8 | 6 | 7 | 20 |
| II | 1 | 3 | 6 | 2 | 40 |
| III | 4 | 7 | 6 | 5 | 30 |
| IV | 6 | 4 | 3 | 5 | 20 |
| Наличие | 40 | 20 | 10 | 40 | 110 |
Найти оптимальный план перевозок и определить его стоимость.
Производство двух видов продукции приносит прибыль в расчете на единицу, соответственно, 6; 5.
Для производства продукции используются ресурсы трех видов в следующих количествах (первое число относится к первому виду продукции, второе ко второму).
Первый ресурс: 1 и 6.
Второй ресурс 3 и 1
Третий ресурс 4 и 7.
Ресурсы имеются в количествах, соответственно: 54; 6 и 42.
Найти программу производства, приносящую наибольшую прибыль.
Производство двух видов продукции приносит прибыль в расчете на единицу, соответственно, 2; 7.
Для производства продукции используются ресурсы трех видов в следующих количествах (первое число относится к первому виду продукции, второе ко второму).
Первый ресурс: 1 и 6.
Второй ресурс: 3 и 1
Третий ресурс: 4 и 7.
Ресурсы имеются в количествах, соответственно: 54; 6 и 42.
Найти наибольшую прибыль.
Найти при каких значениях переменных достигает максимума целевая функция:
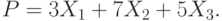
При следующих ограничениях:
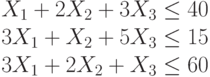
Функция определена только при неотрицательных значениях переменных.
Найти значение максимума целевой функции:
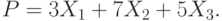
При следующих ограничениях:

Функция определена только при неотрицательных значениях переменных.
Найти при каких значениях фиктивных переменных, вводимых в симплекс методе, достигает максимума целевая функция:
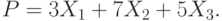
При следующих ограничениях:

Функция определена только при неотрицательных значениях переменных.
Найти при каких значениях переменных достигает максимума целевая функция:
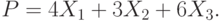
При следующих ограничениях:

Функция определена только при неотрицательных значениях переменных.
Найти значение максимума целевой функции:
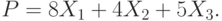
При следующих ограничениях:
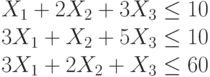
Функция определена только при неотрицательных значениях переменных.
Найти при каких значениях фиктивных переменных, вводимых в симплекс методе, достигает максимума целевая функция:
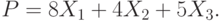
При следующих ограничениях:

Функция определена только при неотрицательных значениях переменных.
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 3 | 1 | 1 | 0 | 10 |
| 0 | 4 | 8 | 0 | 1 | 96 |
| 1 | -4 | -8 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 7 | 1 | 1 | 0 | 10 |
| 0 | 6 | 6 | 0 | 1 | 72 |
| 1 | -4 | -9 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 4 | 1 | 3 | 1 | 0 | 0 | 10 |
| 0 | 6 | 4,5 | 2 | 0 | 1 | 0 | 81 |
| 0 | 1 | 8 | 5 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 7 | 2 | 2 | 1 | 0 | 0 | 10 |
| 0 | 6 | 12 | 6 | 0 | 1 | 0 | 72 |
| 0 | 7 | 16 | 7 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 4 | 9 | 3 | 1 | 0 | 0 | 27 |
| 0 | 6 | 9 | 2 | 0 | 1 | 0 | 81 |
| 0 | 1 | 16 | 5 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 7 | 1 | 1 | 0 | 10 |
| 0 | 4 | 2 | 0 | 1 | 40 |
| 1 | -2 | -8 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 6 | 2 | 4 | 1 | 0 | 0 | 20 |
| 0 | 6 | 6 | 1 | 0 | 1 | 0 | 80 |
| 0 | 2 | 4 | 1 | 0 | 0 | 1 | 160 |
| 1 | -4 | -8 | -4 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 6 | 4 | 1 | 0 | 10 |
| 0 | 4 | 8 | 0 | 1 | 40 |
| 1 | -4 | -8 | 0 | 0 | 0 |
С базы на склад в среднем раз в  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве 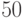 ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением 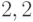 ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 6 | 2 | 4 | 1 | 0 | 0 | 20 |
| 0 | 6 | 6 | 1 | 0 | 1 | 0 | 80 |
| 0 | 2 | 4 | 1 | 0 | 0 | 1 | 160 |
| 1 | -4 | -8 | -4 | 0 | 0 | 0 | 0 |
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 4 | 5 | 1 | 2 | 110 |
| II | 7 | 1 | 8 | 6 | 40 |
| III | 6 | 3 | 3 | 7 | 70 |
| IV | 4 | 2 | 1 | 3 | 50 |
| Наличие | 90 | 40 | 50 | 90 | 270 |
Создать исходный план перевозок методом северо-западного угла и определить его стоимость.
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для второго столбца (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 50 |
| II | | | | 130 |
| III | | | | 20 |
| Наличие | 40 | 70 | 90 | 200 |
Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 10 |
| II | | | | 20 |
| III | | | | 30 |
| Наличие | 15 | 30 | 15 | 60 |
Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 10 |
| II | | | | 20 |
| III | | | | 30 |
| Наличие | 15 | 30 | 15 | 90 |
Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 35 |
| II | | | | 135 |
| III | | | | 25 |
| Наличие | 60 | 60 | 75 | 195 |
Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Найти оптимальный объем партии с точки зрения минимума расходов на приобретение товаров, если цена товара зависит от объема партии  как
как 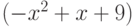 а стоимость хранения как
а стоимость хранения как 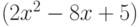 .Ответ округлить до одного знака после запятой.
.Ответ округлить до одного знака после запятой.
Дана матрица левой части системы линейных алгебраических уравнений: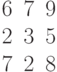 Дан столбец свободных членов:
Дан столбец свободных членов: Найти значение главного определителя системы. Ответ — целое число.
Найти значение главного определителя системы. Ответ — целое число.
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 25 | 20 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 30 |
| II | | | 20 |
| Наличие | 40 | 10 | |
Решить многопродуктовую транспортную задачу.В ответе указать расходы на доставку продукта 2 (целое число).
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 |
|---|
| 0 | 4 | 5 | 7 | | |
| 1 | | | 5 | 5 | |
| 2 | | | 7 | 3 | 6 |
| 3 | | | | 6 | 4 |
| 4 | | | | 1 | 2 |
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 6 | 4 | 2 | 8 | 9 | 12 | 3 | 7 | 3 | 6 |
Найти оценку средней суточной потребности. Ответ -- целое число.
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 5 | 40 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 10 |
| II | | | 20 |
| Наличие | 15 | 15 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 30 |
| Наличие | 50 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать общее количество груза экспедируемого в направлении A-I (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для первого столбца (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 9 | 2 | 3 | 3 |
| II | 3 | 3 | 4 | 5 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 40 |
| II | | | | | 35 |
| III | | | | | 70 |
| IV | | | | | 35 |
| V | | | | | 60 |
| Наличие | 20 | 95 | 50 | 75 | 240 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика B к потребителю III (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 35 |
| II | | | | 135 |
| III | | | | 25 |
| Наличие | 60 | 60 | 75 | 195 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика C к получателю II (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 50 |
| II | | | | 130 |
| III | | | | 20 |
| Наличие | 40 | 70 | 90 | 200 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика A к получателю III (целое число).
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 5 | 40 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 10 |
| II | | | 20 |
| Наличие | 15 | 15 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 30 |
| Наличие | 50 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать расходы на доставку продукта 2 (целое число).
Дана матрица левой части системы линейных алгебраических уравнений: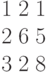 Дан столбец свободных членов:
Дан столбец свободных членов: Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Найти цену, при которой спрос равен предложению, если спрос на товар зависит от цены  как
как  , а предложение как
, а предложение как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.
Найти величину спроса, при котором он равен предложению, если спрос на товар зависит от цены  как
как  , а предложение как
, а предложение как  . Ответ округлить до одного знака после запятой.
. Ответ округлить до одного знака после запятой.
Найти величину предложения, при котором оно равно спросу, если спрос на товар зависит от цены  как
как  , а предложение как
, а предложение как  . Ответ округлить до одного знака после запятой.
. Ответ округлить до одного знака после запятой.
Найти цену, при которой спрос максимален, если спрос на товар зависит от цены  как
как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.
Найти максимальный уровень спроса, если спрос на товар зависит от цены  как
как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.
Найти максимальный уровень спроса, если спрос на товар зависит от цены  как
как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.
Дана матрица левой части системы линейных алгебраических уравнений: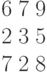 Дан столбец свободных членов:
Дан столбец свободных членов: Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число.
Дана матрица левой части системы линейных алгебраических уравнений: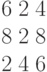 Дан столбец свободных членов:
Дан столбец свободных членов: Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число.
Дана матрица левой части системы линейных алгебраических уравнений: Дан столбец свободных членов:
Дан столбец свободных членов: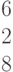 Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число.
Дана матрица левой части системы линейных алгебраических уравнений: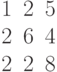 Дан столбец свободных членов:
Дан столбец свободных членов: Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число.
Дана матрица левой части системы линейных алгебраических уравнений: Дан столбец свободных членов:
Дан столбец свободных членов: Найти значение главного определителя системы. Ответ -- целое число.
Найти значение главного определителя системы. Ответ -- целое число.
Дана матрица левой части системы линейных алгебраических уравнений: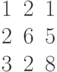 Дан столбец свободных членов:
Дан столбец свободных членов: Найти значение главного определителя системы. Ответ -- целое число.
Найти значение главного определителя системы. Ответ -- целое число.
Дана матрица левой части системы линейных алгебраических уравнений: Дан столбец свободных членов:
Дан столбец свободных членов: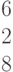 Найти значение главного определителя системы. Ответ -- целое число.
Найти значение главного определителя системы. Ответ -- целое число.
Дана матрица левой части системы линейных алгебраических уравнений: Дан столбец свободных членов:
Дан столбец свободных членов: Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 15 | 4 | 8 | 2 | 7 | 9 | 11 | 6 | 12 | 5 |
Найти оценку дисперсии суточной потребности. Ответ округлить до двух знаков после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 15 | 4 | 8 | 2 | 7 | 9 | 11 | 6 | 12 | 5 |
Найти оценку среднего квадратичного отклонения суточной потребности. Ответ округлить до двух знаков после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 6 | 4 | 2 | 8 | 9 | 12 | 3 | 7 | 3 | 6 |
Найти погрешность оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 9 | 5 | 2 | 7 | 9 | 12 | 5 | 3 | 8 | 4 |
Найти нижнюю границу доверительного интервала
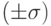
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 15 | 4 | 8 | 2 | 7 | 9 | 11 | 6 | 12 | 5 |
Найти верхнюю границу доверительного интервала
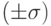
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 15 | 4 | 8 | 2 | 7 | 9 | 11 | 6 | 12 | 5 |
Найти нижнюю границу доверительного интервала

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 15 | 4 | 8 | 2 | 7 | 9 | 11 | 6 | 12 | 5 |
Найти верхнюю границу доверительного интервала

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 80 |
| II | | | | | 55 |
| III | | | | | 110 |
| IV | | | | | 115 |
| V | | | | | 50 |
| Наличие | 60 | 155 | 55 | 140 | 410 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика A к потребителю I (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 9 | 2 | 3 | 3 |
| II | 3 | 3 | 4 | 5 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 40 |
| II | | | | | 35 |
| III | | | | | 70 |
| IV | | | | | 35 |
| V | | | | | 60 |
| Наличие | 20 | 95 | 50 | 75 | 240 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика B к потребителю I (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 80 |
| II | | | | | 55 |
| III | | | | | 110 |
| IV | | | | | 115 |
| V | | | | | 50 |
| Наличие | 60 | 155 | 55 | 140 | 410 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика B к потребителю II (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 80 |
| II | | | | | 55 |
| III | | | | | 110 |
| IV | | | | | 115 |
| V | | | | | 50 |
| Наличие | 60 | 155 | 55 | 140 | 410 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика C к потребителю III (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 90 |
| II | | | | | 45 |
| III | | | | | 130 |
| IV | | | | | 130 |
| V | | | | | 80 |
| Наличие | 50 | 175 | 100 | 150 | 475 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика C к потребителю IV (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 80 |
| II | | | | | 55 |
| III | | | | | 110 |
| IV | | | | | 115 |
| V | | | | | 50 |
| Наличие | 60 | 155 | 55 | 140 | 410 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика D к потребителю IV (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 90 |
| II | | | | | 45 |
| III | | | | | 130 |
| IV | | | | | 130 |
| V | | | | | 80 |
| Наличие | 50 | 175 | 100 | 150 | 475 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика D к потребителю V (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 9 | 2 | 3 | 3 |
| II | 3 | 3 | 4 | 5 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для первой строки (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для второй строки (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 9 | 2 | 3 | 3 |
| II | 3 | 3 | 4 | 5 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для третьей строки (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 9 | 2 | 3 | 3 |
| II | 3 | 3 | 4 | 5 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для четвертой строки (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 9 | 2 | 3 | 3 |
| II | 3 | 3 | 4 | 5 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для пятой строки (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для первого столбца (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 9 | 2 | 3 | 3 |
| II | 3 | 3 | 4 | 5 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для второго столбца (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 9 | 2 | 3 | 3 |
| II | 3 | 3 | 4 | 5 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для третьего столбца (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 20 |
| II | | | | 75 |
| III | | | | 60 |
| Наличие | 35 | 80 | 40 | 155 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика A к получателю I (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 20 |
| II | | | | 75 |
| III | | | | 60 |
| Наличие | 35 | 80 | 40 | 155 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика A к получателю II (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 35 |
| II | | | | 135 |
| III | | | | 25 |
| Наличие | 60 | 60 | 75 | 195 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика A к получателю III (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 20 |
| II | | | | 75 |
| III | | | | 60 |
| Наличие | 35 | 80 | 40 | 155 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика B к получателю I (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 20 |
| II | | | | 75 |
| III | | | | 60 |
| Наличие | 35 | 80 | 40 | 155 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика B к получателю II (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 35 |
| II | | | | 135 |
| III | | | | 25 |
| Наличие | 60 | 60 | 75 | 195 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика B к получателю III (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 50 |
| II | | | | 130 |
| III | | | | 20 |
| Наличие | 40 | 70 | 90 | 200 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика C к получателю II (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 50 |
| II | | | | 130 |
| III | | | | 20 |
| Наличие | 40 | 70 | 90 | 200 |
Решить транспортную задачу. В ответе указать минимальные расходы на перевозку (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 50 |
| II | | | | 130 |
| III | | | | 20 |
| Наличие | 40 | 70 | 90 | 200 |
Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 50 |
| II | | | | 130 |
| III | | | | 20 |
| Наличие | 40 | 70 | 90 | 200 |
Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 40 |
| II | | | | 120 |
| III | | | | 10 |
| Наличие | 30 | 60 | 80 | 170 |
Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 35 |
| II | | | | 100 |
| III | | | | 25 |
| Наличие | 60 | 60 | 40 | 160 |
Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 10 |
| II | | | | 65 |
| III | | | | 50 |
| Наличие | 35 | 60 | 30 | 125 |
Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 50 |
| Наличие | 40 | 30 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 35 |
| Наличие | 55 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать общее количество груза экспедируемого в направлении B-I (целое число).
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 25 | 20 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 30 |
| II | | | 20 |
| Наличие | 40 | 10 | |
Решить многопродуктовую транспортную задачу.В ответе указать общее количество груза экспедируемого в направлении A-II (целое число).
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 50 |
| Наличие | 40 | 30 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 35 |
| Наличие | 55 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать общее количество груза экспедируемого в направлении B-II (целое число).
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 50 |
| Наличие | 40 | 30 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 35 |
| Наличие | 55 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать расходы на доставку продукта 1 (целое число).
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 50 |
| Наличие | 40 | 30 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 35 |
| Наличие | 55 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать расходы на доставку продукта 2 (целое число).
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 25 | 20 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 30 |
| II | | | 20 |
| Наличие | 40 | 10 | |
Решить многопродуктовую транспортную задачу.В ответе указать расходы на доставку продукта 3 (целое число).
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 50 |
| Наличие | 40 | 30 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 35 |
| Наличие | 55 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать общие расходы на доставку всех трех продуктов (целое число).
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 |
|---|
| 0 | 4 | 5 | 7 | |
| 1 | | | 5 | 5 |
| 2 | | | 7 | 3 |
| 3 | | | | 6 |
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 |
|---|
| 0 | 2 | 6 | 7 | | |
| 1 | | 4 | 3 | 3 | |
| 2 | | | 2 | 2 | 1 |
| 3 | | | | 9 | 9 |
| 4 | | | | | 1 |
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 | 6 |
|---|
| 0 | 4 | 5 | 7 | | | |
| 1 | | | 5 | 5 | | |
| 2 | | | 7 | 3 | 6 | |
| 3 | | | | 6 | 4 | |
| 4 | | | | 1 | 2 | 5 |
| 5 | | | | | | 7 |
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|
| 0 | 4 | 5 | 7 | | | | |
| 1 | | | 5 | 5 | | | |
| 2 | | | 7 | 3 | 6 | | |
| 3 | | | | 6 | 4 | | |
| 4 | | | | 1 | 2 | 5 | 8 |
| 5 | | | | | | 7 | 2 |
| 6 | | | | | | | 5 |
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 0 | 4 | 5 | 7 | | | | | |
| 1 | | | 5 | 5 | | | | |
| 2 | | | 7 | 3 | 6 | | | |
| 3 | | | | 6 | 4 | | | |
| 4 | | | | 1 | 2 | 5 | 8 | |
| 5 | | | | | | 7 | 2 | 3 |
| 6 | | | | | | | 5 | 7 |
| 7 | | | | | | | | 9 |
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|
| 0 | 2 | 6 | 7 | | | | | | |
| 1 | | 4 | 3 | 3 | | | | | |
| 2 | | | 2 | 2 | 1 | | | | |
| 3 | | | | 9 | 9 | | | | |
| 4 | | | | | 3 | 3 | 4 | | |
| 5 | | | | | | 8 | 7 | 7 | |
| 6 | | | | | | | 1 | 5 | 9 |
| 7 | | | | | | | | 3 | 5 |
| 8 | | | | | | | | | 3 |
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|
| 0 | 4 | 5 | 7 | | | | | | | |
| 1 | | | 5 | 5 | | | | | | |
| 2 | | | 7 | 3 | 6 | | | | | |
| 3 | | | | 6 | 4 | | | | | |
| 4 | | | | 1 | 2 | 5 | 8 | | | |
| 5 | | | | | | 7 | 2 | 3 | | |
| 6 | | | | | | | 5 | 7 | 4 | |
| 7 | | | | | | | | 9 | 3 | |
| 8 | | | | | | | | | 7 | 4 |
| 9 | | | | | | | | | | 6 |
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 9 | 5 | 2 | 7 | 9 | 12 | 5 | 3 | 8 | 4 |
Найти оценку среднего квадратичного отклонения суточной потребности. Ответ округлить до двух знаков после запятой.
Задана таблица транспортных тарифов.
| A | B | C | D |
| I | 9 | 2 | 3 | 3 |
| II | 5 | 7 | 2 | 6 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
| I | | | | | 40 |
| II | | | | | 35 |
| III | | | | | 70 |
| IV | | | | | 35 |
| V | | | | | 60 |
| Наличие | 20 | 95 | 50 | 75 | 240 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика A к потребителю I (целое число).
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 50 |
| Наличие | 40 | 30 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 35 |
| Наличие | 55 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать расходы на доставку продукта 2 (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 35 |
| II | | | | 135 |
| III | | | | 25 |
| Наличие | 60 | 60 | 75 | 195 |
Решить транспортную задачу. В ответе указать минимальные расходы на перевозку (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 10 |
| II | | | | 65 |
| III | | | | 50 |
| Наличие | 35 | 60 | 30 | 125 |
Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 6 | 4 | 2 | 8 | 9 | 12 | 3 | 7 | 3 | 6 |
Найти оценку дисперсии суточной потребности. Ответ округлить до одного знака после запятой.
Найти максимальный уровень спроса, если спрос на товар зависит от цены  как
как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.
Дана матрица левой части системы линейных алгебраических уравнений: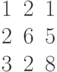 Дан столбец свободных членов:
Дан столбец свободных членов: Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число.
Дана матрица левой части системы линейных алгебраических уравнений: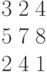 Дан столбец свободных членов:
Дан столбец свободных членов: Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число.
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 40 |
| II | | | | 120 |
| III | | | | 10 |
| Наличие | 30 | 60 | 80 | 170 |
Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 50 |
| Наличие | 40 | 30 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 35 |
| Наличие | 55 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать общее количество груза экспедируемого в направлении A-II (целое число).
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 15 | 4 | 8 | 2 | 7 | 9 | 11 | 6 | 12 | 5 |
Найти погрешность оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 80 |
| II | | | | | 55 |
| III | | | | | 110 |
| IV | | | | | 115 |
| V | | | | | 50 |
| Наличие | 60 | 155 | 55 | 140 | 410 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика B к потребителю I (целое число).
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 2 | 2 | 1 | 0 | 30 |
| 0 | 8 | 6 | 0 | 1 | 80 |
| 1 | -2 | -6 | 0 | 0 | 0 |
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 20 |
| II | | | | 75 |
| III | | | | 60 |
| Наличие | 35 | 80 | 40 | 155 |
Решить транспортную задачу. В ответе указать минимальные расходы на перевозку (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 35 |
| II | | | | 100 |
| III | | | | 25 |
| Наличие | 60 | 60 | 40 | 160 |
Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|
| 0 | 2 | 6 | 7 | | | | |
| 1 | | 4 | 3 | 3 | | | |
| 2 | | | 2 | 2 | 1 | | |
| 3 | | | | 9 | 9 | | |
| 4 | | | | | 3 | 3 | 4 |
| 5 | | | | | | 8 | 7 |
| 6 | | | | | | | 1 |
С базы на склад в среднем раз в  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
Задана таблица транспортных тарифов.
| A | B | C | D |
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
| I | | | | | 90 |
| II | | | | | 45 |
| III | | | | | 130 |
| IV | | | | | 130 |
| V | | | | | 80 |
| Наличие | 50 | 175 | 100 | 150 | 475 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика C к потребителю III (целое число).
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 3 | 7 | 4 | 6 | 60 |
| II | 2 | 4 | 3 | 3 | 30 |
| III | 3 | 5 | 6 | 3 | 30 |
| IV | 5 | 5 | 2 | 6 | 30 |
| Наличие | 10 | 70 | 50 | 20 | 150 |
Найти оптимальный план перевозок и определить его стоимость.
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 35 |
| II | | | | 135 |
| III | | | | 25 |
| Наличие | 60 | 60 | 75 | 195 |
Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 | 6 |
|---|
| 0 | 2 | 6 | 7 | | | |
| 1 | | 4 | 3 | 3 | | |
| 2 | | | 2 | 2 | 1 | |
| 3 | | | | 9 | 9 | |
| 4 | | | | | 3 | 3 |
| 5 | | | | | | 8 |
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 6 | 4 | 2 | 8 | 9 | 12 | 3 | 7 | 3 | 6 |
Найти оценку среднего квадратичного отклонения суточной потребности. Ответ округлить до двух знаков после запятой.
Найти величину предложения, при котором оно равно спросу, если спрос на товар зависит от цены  как
как  , а предложение как
, а предложение как  . Ответ округлить до одного знака после запятой.
. Ответ округлить до одного знака после запятой.
Дана матрица левой части системы линейных алгебраических уравнений: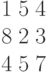 Дан столбец свободных членов:
Дан столбец свободных членов: Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число.
Дана матрица левой части системы линейных алгебраических уравнений: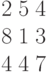 Дан столбец свободных членов:
Дан столбец свободных членов: Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число.
Дана матрица левой части системы линейных алгебраических уравнений: Дан столбец свободных членов:
Дан столбец свободных членов: Найти значение главного определителя системы. Ответ — целое число.
Найти значение главного определителя системы. Ответ — целое число.
Дана матрица левой части системы линейных алгебраических уравнений: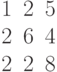 Дан столбец свободных членов:
Дан столбец свободных членов: Найти значение главного определителя системы. Ответ -- целое число.
Найти значение главного определителя системы. Ответ -- целое число.
Дана матрица левой части системы линейных алгебраических уравнений: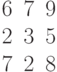 Дан столбец свободных членов:
Дан столбец свободных членов: Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 15 | 4 | 8 | 2 | 7 | 9 | 11 | 6 | 12 | 5 |
Найти оценку средней суточной потребности. Ответ округлить до одного знака после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 9 | 5 | 2 | 7 | 9 | 12 | 5 | 3 | 8 | 4 |
Найти оценку дисперсии суточной потребности. Ответ округлить до двух знаков после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 6 | 4 | 2 | 8 | 9 | 12 | 3 | 7 | 3 | 6 |
Найти оценку среднего квадратичного отклонения суточной потребности. Ответ округлить до двух знаков после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 9 | 5 | 2 | 7 | 9 | 12 | 5 | 3 | 8 | 4 |
Найти верхнюю границу доверительного интервала
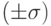
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 6 | 4 | 2 | 8 | 9 | 12 | 3 | 7 | 3 | 6 |
Найти нижнюю границу доверительного интервала

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
С базы на склад в среднем раз в 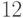 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в 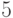 ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
С базы на склад в среднем раз в  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением 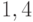 ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 9 | 2 | 3 | 3 |
| II | 3 | 3 | 4 | 5 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 40 |
| II | | | | | 35 |
| III | | | | | 70 |
| IV | | | | | 35 |
| V | | | | | 60 |
| Наличие | 20 | 95 | 50 | 75 | 240 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика B к потребителю II (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 90 |
| II | | | | | 45 |
| III | | | | | 130 |
| IV | | | | | 130 |
| V | | | | | 80 |
| Наличие | 50 | 175 | 100 | 150 | 475 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика C к потребителю III (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 9 | 2 | 3 | 3 |
| II | 3 | 3 | 4 | 5 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 40 |
| II | | | | | 35 |
| III | | | | | 70 |
| IV | | | | | 35 |
| V | | | | | 60 |
| Наличие | 20 | 95 | 50 | 75 | 240 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика C к потребителю IV (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 9 | 2 | 3 | 3 |
| II | 3 | 3 | 4 | 5 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 40 |
| II | | | | | 35 |
| III | | | | | 70 |
| IV | | | | | 35 |
| V | | | | | 60 |
| Наличие | 20 | 95 | 50 | 75 | 240 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика D к потребителю IV (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 80 |
| II | | | | | 55 |
| III | | | | | 110 |
| IV | | | | | 115 |
| V | | | | | 50 |
| Наличие | 60 | 155 | 55 | 140 | 410 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика D к потребителю V (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для первой строки (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для второй строки (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для третьей строки (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для четвертой строки (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 9 | 2 | 3 | 3 |
| II | 3 | 3 | 4 | 5 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для первого столбца (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для второго столбца (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 35 |
| II | | | | 135 |
| III | | | | 25 |
| Наличие | 60 | 60 | 75 | 195 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика A к получателю I (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 50 |
| II | | | | 130 |
| III | | | | 20 |
| Наличие | 40 | 70 | 90 | 200 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика A к получателю II (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 35 |
| II | | | | 135 |
| III | | | | 25 |
| Наличие | 60 | 60 | 75 | 195 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика B к получателю I (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 25 |
| II | | | | 125 |
| III | | | | 15 |
| Наличие | 50 | 50 | 65 | 165 |
Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 25 |
| II | | | | 90 |
| III | | | | 15 |
| Наличие | 50 | 50 | 30 | 130 |
Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 25 |
| II | | | | 125 |
| III | | | | 15 |
| Наличие | 50 | 50 | 65 | 165 |
Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 10 |
| II | | | | 35 |
| III | | | | 5 |
| Наличие | 25 | 5 | 20 | 50 |
Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 5 | 40 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 10 |
| II | | | 20 |
| Наличие | 15 | 15 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 30 |
| Наличие | 50 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать общее количество груза экспедируемого в направлении B-I (целое число).
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 5 | 40 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 10 |
| II | | | 20 |
| Наличие | 15 | 15 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 30 |
| Наличие | 50 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать общее количество груза экспедируемого в направлении A-II (целое число).
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 25 | 20 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 30 |
| II | | | 20 |
| Наличие | 40 | 10 | |
Решить многопродуктовую транспортную задачу.В ответе указать общее количество груза экспедируемого в направлении B-II (целое число).
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 50 |
| Наличие | 40 | 30 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 35 |
| Наличие | 55 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать общее количество груза экспедируемого в направлении A-I (целое число).
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 4 | 8 | 6 | 7 | 100 |
| II | 1 | 3 | 6 | 2 | 40 |
| III | 4 | 7 | 6 | 5 | 60 |
| IV | 6 | 4 | 3 | 5 | 50 |
| Наличие | 80 | 40 | 40 | 90 | 250 |
Найти оптимальный план перевозок и определить его стоимость.
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 8 | 6 | 4 | 6 | 70 |
| II | 2 | 7 | 2 | 3 | 30 |
| III | 5 | 7 | 8 | 3 | 40 |
| IV | 8 | 5 | 2 | 3 | 60 |
| Наличие | 80 | 10 | 50 | 60 | 200 |
Создать исходный план перевозок методом северо-западного угла и определить его стоимость.
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 4 | 9 | 5 | 7 | 20 |
| II | 1 | 3 | 5 | 2 | 40 |
| III | 4 | 7 | 3 | 5 | 30 |
| IV | 6 | 4 | 3 | 5 | 20 |
| Наличие | 40 | 20 | 10 | 40 | 110 |
Найти оптимальный план перевозок и определить его стоимость.
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 2 | 3 | 4 | 5 | 60 |
| II | 1 | 2 | 4 | 6 | 30 |
| III | 3 | 1 | 5 | 1 | 30 |
| IV | 4 | 1 | 2 | 4 | 30 |
| Наличие | 10 | 70 | 50 | 20 | 150 |
Найти оптимальный план перевозок и определить его стоимость.
Найти значение максимума целевой функции:
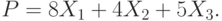
При следующих ограничениях:
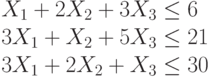
Функция определена только при неотрицательных значениях переменных.
Найти при каких значениях фиктивных переменных, вводимых в симплекс методе, достигает максимума целевая функция:
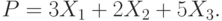
При следующих ограничениях:

Функция определена только при неотрицательных значениях переменных.
Найти значение максимума целевой функции:
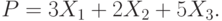
При следующих ограничениях:
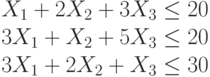
Функция определена только при неотрицательных значениях переменных.
Найти при каких значениях фиктивных переменных, вводимых в симплекс методе, достигает максимума целевая функция:
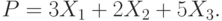
При следующих ограничениях:
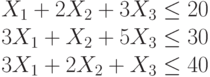
Функция определена только при неотрицательных значениях переменных.
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 4 | 1 | 1 | 0 | 5 |
| 0 | 2 | 9 | 0 | 1 | 45 |
| 1 | -4 | -5 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 4 | 1 | 1 | 0 | 10 |
| 0 | 6 | 5 | 0 | 1 | 96 |
| 1 | -1 | -7 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 7 | 1 | 2 | 1 | 0 | 0 | 10 |
| 0 | 6 | 6 | 6 | 0 | 1 | 0 | 72 |
| 0 | 7 | 8 | 7 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 3 | 4 | 4 | 1 | 0 | 0 | 10 |
| 0 | 2 | 12 | 6 | 0 | 1 | 0 | 72 |
| 0 | 5 | 35 | 1 | 0 | 0 | 1 | 140 |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 3 | 5 | 4 | 1 | 0 | 0 | 25 |
| 0 | 2 | 12 | 6 | 0 | 1 | 0 | 72 |
| 0 | 5 | 35 | 1 | 0 | 0 | 1 | 280 |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 5 | 2 | 1 | 0 | 20 |
| 0 | 3 | 1 | 0 | 1 | 35 |
| 1 | -4 | -6 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 2 | 2 | 4 | 1 | 0 | 0 | 20 |
| 0 | 6 | 1 | 1 | 0 | 1 | 0 | 60 |
| 0 | 2 | 4 | 1 | 0 | 0 | 1 | 140 |
| 1 | -6 | -8 | -4 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 8 | 2 | 1 | 0 | 25 |
| 0 | 4 | 8 | 0 | 1 | 65 |
| 1 | -6 | -8 | 0 | 0 | 0 |
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 |
|---|
| 0 | 5 | 3 | 4 | |
| 1 | | 2 | 2 | 7 |
| 2 | | | 4 | 6 |
| 3 | | | | 3 |
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|
| 0 | 5 | 3 | 4 | | | | | | | |
| 1 | | 2 | 2 | 7 | | | | | | |
| 3 | | | | 3 | 5 | | | | | |
| 4 | | | | | 3 | 7 | 2 | | | |
| 5 | | | | | | 9 | 3 | 2 | | |
| 6 | | | | | | | 4 | 4 | 3 | |
| 7 | | | | | | | | 6 | 2 | |
| 8 | | | | | | | | | 6 | 5 |
| 9 | | | | | | | | | | 2 |
С базы на склад в среднем раз в  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве 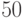 ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
С базы на склад в среднем раз в  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в 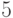 ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением 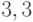 ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  день. Известно, что к началу первого дня остаток на складе составлял
день. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 35 |
| II | | | | 135 |
| III | | | | 25 |
| Наличие | 60 | 60 | 75 | 195 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика B к получателю II (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 90 |
| II | | | | | 45 |
| III | | | | | 130 |
| IV | | | | | 130 |
| V | | | | | 80 |
| Наличие | 50 | 175 | 100 | 150 | 475 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика B к потребителю I (целое число).
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 15 | 4 | 8 | 2 | 7 | 9 | 11 | 6 | 12 | 5 |
Найти оценку среднего квадратичного отклонения суточной потребности. Ответ округлить до двух знаков после запятой.
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 |
|---|
| 0 | 2 | 6 | 7 | |
| 1 | | 4 | 3 | 3 |
| 2 | | | 2 | 2 |
| 3 | | | | 9 |
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|
| 0 | 5 | 3 | 4 | | | | |
| 1 | | 2 | 2 | 7 | | | |
| 2 | | | 4 | 6 | 2 | | |
| 3 | | | | 3 | 5 | | |
| 4 | | | | | 3 | 7 | 2 |
| 5 | | | | | | 9 | 3 |
| 6 | | | | | | | 4 |
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 4 | 9 | 5 | 7 | 100 |
| II | 1 | 3 | 5 | 2 | 40 |
| III | 4 | 7 | 3 | 5 | 60 |
| IV | 6 | 4 | 3 | 5 | 50 |
| Наличие | 80 | 40 | 40 | 90 | 250 |
Найти оптимальный план перевозок и определить его стоимость.
Найти при каких значениях переменных достигает максимума целевая функция:
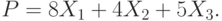
При следующих ограничениях:
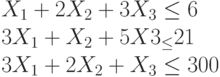
Функция определена только при неотрицательных значениях переменных.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 9 | 5 | 2 | 7 | 9 | 12 | 5 | 3 | 8 | 4 |
Найти оценку среднего квадратичного отклонения суточной потребности. Ответ округлить до двух знаков после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 6 | 4 | 2 | 8 | 9 | 12 | 3 | 7 | 3 | 6 |
Найти верхнюю границу доверительного интервала

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 8 | 5 | 1 | 0 | 20 |
| 0 | 2 | 3 | 0 | 1 | 50 |
| 1 | -4 | -6 | 0 | 0 | 0 |
Найти цену, при которой спрос максимален, если спрос на товар зависит от цены  как
как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 5 | 40 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 10 |
| II | | | 20 |
| Наличие | 15 | 15 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 30 |
| Наличие | 50 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать расходы на доставку продукта 3 (целое число).
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 6 | 4 | 2 | 8 | 9 | 12 | 3 | 7 | 3 | 6 |
Найти нижнюю границу доверительного интервала
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
Найти максимальный уровень спроса, если спрос на товар зависит от цены  как
как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.
Найти цену, при которой спрос равен предложению, если спрос на товар зависит от цены  как
как  , а предложение как
, а предложение как  . Ответ округлить до одного знака после запятой.
. Ответ округлить до одного знака после запятой.
Найти цену, при которой спрос максимален, если спрос на товар зависит от цены  как
как  . Ответ округлить до одного знака после запятой.
. Ответ округлить до одного знака после запятой.
Найти максимальный уровень спроса, если спрос на товар зависит от цены  как
как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.
Дана матрица левой части системы линейных алгебраических уравнений: Дан столбец свободных членов:
Дан столбец свободных членов: Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число.
Дана матрица левой части системы линейных алгебраических уравнений: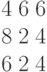 Дан столбец свободных членов:
Дан столбец свободных членов: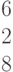 Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 9 | 5 | 2 | 7 | 9 | 12 | 5 | 3 | 8 | 4 |
Найти погрешность оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 15 | 4 | 8 | 2 | 7 | 9 | 11 | 6 | 12 | 5 |
Найти нижнюю границу доверительного интервала
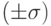
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 6 | 4 | 2 | 8 | 9 | 12 | 3 | 7 | 3 | 6 |
Найти верхнюю границу доверительного интервала
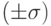
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 9 | 5 | 2 | 7 | 9 | 12 | 5 | 3 | 8 | 4 |
Найти нижнюю границу доверительного интервала

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
С базы на склад в среднем раз в 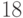 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве 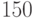 ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в 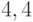 ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением 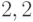 ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 90 |
| II | | | | | 45 |
| III | | | | | 130 |
| IV | | | | | 130 |
| V | | | | | 80 |
| Наличие | 50 | 175 | 100 | 150 | 475 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика B к потребителю II (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 90 |
| II | | | | | 45 |
| III | | | | | 130 |
| IV | | | | | 130 |
| V | | | | | 80 |
| Наличие | 50 | 175 | 100 | 150 | 475 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика B к потребителю III (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 80 |
| II | | | | | 55 |
| III | | | | | 110 |
| IV | | | | | 115 |
| V | | | | | 50 |
| Наличие | 60 | 155 | 55 | 140 | 410 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика C к потребителю IV (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 90 |
| II | | | | | 45 |
| III | | | | | 130 |
| IV | | | | | 130 |
| V | | | | | 80 |
| Наличие | 50 | 175 | 100 | 150 | 475 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика D к потребителю IV (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для третьей строки (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для третьего столбца (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 35 |
| II | | | | 135 |
| III | | | | 25 |
| Наличие | 60 | 60 | 75 | 195 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика A к получателю II (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 20 |
| II | | | | 75 |
| III | | | | 60 |
| Наличие | 35 | 80 | 40 | 155 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика A к получателю III (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 20 |
| II | | | | 75 |
| III | | | | 60 |
| Наличие | 35 | 80 | 40 | 155 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика C к получателю II (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 20 |
| II | | | | 30 |
| III | | | | 40 |
| Наличие | 25 | 40 | 25 | 90 |
Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 25 |
| II | | | | 90 |
| III | | | | 15 |
| Наличие | 50 | 50 | 30 | 130 |
Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 5 | 40 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 10 |
| II | | | 20 |
| Наличие | 15 | 15 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 30 |
| Наличие | 50 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать общее количество груза экспедируемого в направлении B-II (целое число).
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 2 | 3 | 4 | 5 | 100 |
| II | 1 | 2 | 4 | 6 | 40 |
| III | 3 | 1 | 5 | 1 | 60 |
| IV | 4 | 1 | 2 | 4 | 50 |
| Наличие | 80 | 40 | 40 | 90 | 250 |
Найти оптимальный план перевозок и определить его стоимость.
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 3 | 7 | 4 | 6 | 60 |
| II | 2 | 4 | 3 | 3 | 30 |
| III | 3 | 5 | 6 | 3 | 30 |
| IV | 5 | 5 | 2 | 6 | 30 |
| Наличие | 10 | 70 | 50 | 20 | 150 |
Создать исходный план перевозок методом северо-западного угла и определить его стоимость.
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 4 | 5 | 1 | 2 | 70 |
| II | 7 | 1 | 8 | 6 | 30 |
| III | 6 | 3 | 3 | 7 | 40 |
| IV | 4 | 2 | 1 | 3 | 60 |
| Наличие | 80 | 10 | 50 | 60 | 200 |
Найти оптимальный план перевозок и определить его стоимость.
Найти при каких значениях переменных достигает максимума целевая функция:
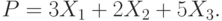
При следующих ограничениях:

Функция определена только при неотрицательных значениях переменных.
Найти при каких значениях переменных достигает максимума целевая функция:
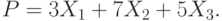
При следующих ограничениях:
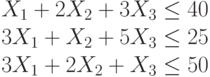
Функция определена только при неотрицательных значениях переменных.
Найти значение максимума целевой функции:
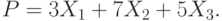
При следующих ограничениях:
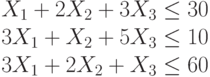
Функция определена только при неотрицательных значениях переменных.
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 0 | 5 | 3 | 4 | | | | | |
| 1 | | 2 | 2 | 7 | | | | |
| 2 | | | 4 | 6 | 2 | | | |
| 3 | | | | 3 | 5 | | | |
| 4 | | | | | 3 | 7 | 2 | |
| 5 | | | | | | 9 | 3 | 2 |
| 6 | | | | | | | 4 | 4 |
| 7 | | | | | | | | 6 |
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 5 | 40 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 10 |
| II | | | 20 |
| Наличие | 15 | 15 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 30 |
| Наличие | 50 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать общие расходы на доставку всех трех продуктов (целое число).
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 8 | 6 | 4 | 6 | 110 |
| II | 2 | 7 | 2 | 3 | 40 |
| III | 5 | 7 | 8 | 3 | 70 |
| IV | 8 | 5 | 2 | 3 | 50 |
| Наличие | 90 | 40 | 50 | 90 | 270 |
Найти оптимальный план перевозок и определить его стоимость.
С базы на склад в среднем раз в 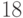 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве 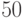 ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в 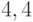 ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  день. Известно, что к началу первого дня остаток на складе составлял
день. Известно, что к началу первого дня остаток на складе составлял 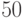 ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 5 | 40 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 10 |
| II | | | 20 |
| Наличие | 15 | 15 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 30 |
| Наличие | 50 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать расходы на доставку продукта 2 (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 50 |
| II | | | | 130 |
| III | | | | 20 |
| Наличие | 40 | 70 | 90 | 200 |
Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для третьего столбца (целое число).
Дана матрица левой части системы линейных алгебраических уравнений: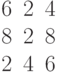 Дан столбец свободных членов:
Дан столбец свободных членов: Найти значение главного определителя системы. Ответ -- целое число.
Найти значение главного определителя системы. Ответ -- целое число.
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 25 | 20 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 30 |
| II | | | 20 |
| Наличие | 40 | 10 | |
Решить многопродуктовую транспортную задачу.В ответе указать расходы на доставку продукта 1 (целое число).
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 50 |
| Наличие | 40 | 30 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 35 |
| Наличие | 55 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать расходы на доставку продукта 3 (целое число).
С базы на склад в среднем раз в 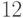 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в 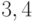 ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 9 | 5 | 2 | 7 | 9 | 12 | 5 | 3 | 8 | 4 |
Найти верхнюю границу доверительного интервала

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
Найти величину спроса, при котором он равен предложению, если спрос на товар зависит от цены  как
как  , а предложение как
, а предложение как  . Ответ округлить до одного знака после запятой.
. Ответ округлить до одного знака после запятой.
Дана матрица левой части системы линейных алгебраических уравнений: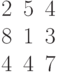 Дан столбец свободных членов:
Дан столбец свободных членов: Найти значение главного определителя системы. Ответ -- целое число.
Найти значение главного определителя системы. Ответ -- целое число.
Даны данные за 10 дней о потребности в материальном ресурсе.
 | 9 | 5 | 2 | 7 | 9 | 12 | 5 | 3 | 8 | 4 |
Найти оценку средней суточной потребности. Ответ округлить до одного знака после запятой.
С базы на склад в среднем раз в  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве 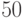 ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением 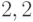 ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
С базы на склад в среднем раз в  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в 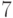 ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 90 |
| II | | | | | 45 |
| III | | | | | 130 |
| IV | | | | | 130 |
| V | | | | | 80 |
| Наличие | 50 | 175 | 100 | 150 | 475 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика A к потребителю I (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 80 |
| II | | | | | 55 |
| III | | | | | 110 |
| IV | | | | | 115 |
| V | | | | | 50 |
| Наличие | 60 | 155 | 55 | 140 | 410 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика B к потребителю III (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 9 | 2 | 3 | 3 |
| II | 3 | 3 | 4 | 5 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 40 |
| II | | | | | 35 |
| III | | | | | 70 |
| IV | | | | | 35 |
| V | | | | | 60 |
| Наличие | 20 | 95 | 50 | 75 | 240 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика D к потребителю V (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 9 | 2 | 3 | 3 |
| II | 3 | 3 | 4 | 5 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для второй строки (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для четвертой строки (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 50 |
| II | | | | 130 |
| III | | | | 20 |
| Наличие | 40 | 70 | 90 | 200 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика B к получателю II (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 20 |
| II | | | | 75 |
| III | | | | 60 |
| Наличие | 35 | 80 | 40 | 155 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика B к получателю III (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 20 |
| II | | | | 75 |
| III | | | | 60 |
| Наличие | 35 | 80 | 40 | 155 |
Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 5 | 40 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 10 |
| II | | | 20 |
| Наличие | 15 | 15 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 35 |
| II | | | 30 |
| Наличие | 50 | 15 | |
Решить многопродуктовую транспортную задачу.В ответе указать расходы на доставку продукта 1 (целое число).
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 3 | 7 | 4 | 6 | 100 |
| II | 2 | 4 | 3 | 3 | 40 |
| III | 3 | 5 | 6 | 3 | 60 |
| IV | 5 | 5 | 2 | 6 | 50 |
| Наличие | 80 | 40 | 40 | 90 | 250 |
Создать исходный план перевозок методом северо-западного угла и определить его стоимость.
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 4 | 5 | 1 | 2 | 70 |
| II | 7 | 1 | 8 | 6 | 30 |
| III | 6 | 3 | 3 | 7 | 40 |
| IV | 4 | 2 | 1 | 3 | 60 |
| Наличие | 80 | 10 | 50 | 60 | 200 |
Создать исходный план перевозок методом северо-западного угла и определить его стоимость.
Производство двух видов продукции приносит прибыль в расчете на единицу, соответственно, 2; 7.
Для производства продукции используются ресурсы трех видов в следующих количествах (первое число относится к первому виду продукции, второе ко второму).
Первый ресурс: 1 и 6.
Второй ресурс: 3 и 1
Третий ресурс: 4 и 7.
Ресурсы имеются в количествах, соответственно: 54; 6 и 42.
Найти программу производства, приносящую наибольшую прибыль.
Производство двух видов продукции приносит прибыль в расчете на единицу, соответственно, 5; 4.
Для производства продукции используются ресурсы трех видов в следующих количествах (первое число относится к первому виду продукции, второе ко второму).
Первый ресурс: 1 и 6.
Второй ресурс 3 и 1
Третий ресурс 4 и 7.
Ресурсы имеются в количествах, соответственно: 54; 6 и 42.
Найти наибольшую прибыль.
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 3 | 1 | 1 | 0 | 5 |
| 0 | 6 | 5 | 0 | 1 | 45 |
| 1 | -3 | -7 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 4 | 5 | 3 | 1 | 0 | 0 | 10 |
| 0 | 6 | 9 | 2 | 0 | 1 | 0 | 81 |
| 0 | 1 | 16 | 5 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 2 | 2 | 4 | 1 | 0 | 0 | 30 |
| 0 | 8 | 1 | 1 | 0 | 1 | 0 | 45 |
| 0 | 1 | 4 | 1 | 0 | 0 | 1 | 120 |
| 1 | -8 | -4 | -4 | 0 | 0 | 0 | 0 |
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 50 |
| II | | | | 130 |
| III | | | | 20 |
| Наличие | 40 | 70 | 90 | 200 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика B к получателю I (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 7 | 3 | 5 | 2 |
| II | 4 | 1 | 6 | 4 |
| III | 5 | 8 | 3 | 5 |
| IV | 8 | 7 | 6 | 2 |
| V | 5 | 3 | 1 | 4 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для пятой строки (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для первой строки (целое число).
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для пятой строки (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 20 |
| II | | | | 30 |
| III | | | | 40 |
| Наличие | 25 | 40 | 25 | 90 |
Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 20 |
| II | | | | 75 |
| III | | | | 60 |
| Наличие | 35 | 80 | 40 | 155 |
Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 4 | 1 | 1 | 0 | 10 |
| 0 | 2 | 6 | 0 | 1 | 72 |
| 1 | -3 | -6 | 0 | 0 | 0 |
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 7 | 3 | 2 | 1 | 0 | 0 | 15 |
| 0 | 6 | 12 | 6 | 0 | 1 | 0 | 72 |
| 0 | 7 | 16 | 7 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 | 6 |
|---|
| 0 | 5 | 3 | 4 | | | |
| 1 | | 2 | 2 | 7 | | |
| 2 | | | 4 | 6 | 2 | |
| 3 | | | | 3 | 5 | |
| 4 | | | | | 3 | 7 |
| 5 | | | | | | 9 |
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|
| 0 | 5 | 3 | 4 | | | | | | |
| 1 | | 2 | 2 | 7 | | | | | |
| 2 | | | 4 | 6 | 2 | | | | |
| 3 | | | | 3 | 5 | | | | |
| 4 | | | | | 3 | 7 | 2 | | |
| 5 | | | | | | 9 | 3 | 2 | |
| 6 | | | | | | | 4 | 4 | 3 |
| 7 | | | | | | | | 6 | 2 |
| 8 | | | | | | | | | 6 |
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|
| 0 | 2 | 6 | 7 | | | | | | | |
| 1 | | 4 | 3 | 3 | | | | | | |
| 2 | | | 2 | 2 | 1 | | | | | |
| 3 | | | | 9 | 9 | | | | | |
| 4 | | | | | 3 | 3 | 4 | | | |
| 5 | | | | | | 8 | 7 | 7 | | |
| 6 | | | | | | | 1 | 5 | 9 | |
| 7 | | | | | | | | 3 | 5 | |
| 8 | | | | | | | | | 3 | 9 |
| 9 | | | | | | | | | | 3 |
Дана матрица левой части системы линейных алгебраических уравнений: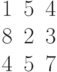 Дан столбец свободных членов:
Дан столбец свободных членов: Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Найти при каких значениях фиктивных переменных, вводимых в симплекс методе, достигает максимума целевая функция:
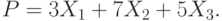
При следующих ограничениях:
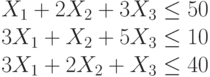
Функция определена только при неотрицательных значениях переменных.
Найти величину предложения, при котором оно равно спросу, если спрос на товар зависит от цены  как
как 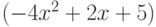 , а предложение как
, а предложение как 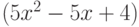 . Ответ округлить до одного знака после запятой.
. Ответ округлить до одного знака после запятой.
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 50 |
| II | | | | 130 |
| III | | | | 20 |
| Наличие | 40 | 70 | 90 | 200 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика A к получателю I (целое число).
Дана матрица левой части системы линейных алгебраических уравнений: Дан столбец свободных членов:
Дан столбец свободных членов: Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 9 | 2 | 3 | 3 |
| II | 3 | 3 | 4 | 5 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 40 |
| II | | | | | 35 |
| III | | | | | 70 |
| IV | | | | | 35 |
| V | | | | | 60 |
| Наличие | 20 | 95 | 50 | 75 | 240 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика A к потребителю I (целое число).
Найти значение максимума целевой функции:
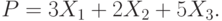
При следующих ограничениях:

Функция определена только при неотрицательных значениях переменных.
Найти при каких значениях переменных достигает максимума целевая функция:
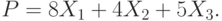
При следующих ограничениях:
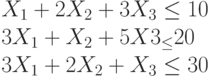
Функция определена только при неотрицательных значениях переменных.
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 0 | 2 | 6 | 7 | | | | | |
| 1 | | 4 | 3 | 3 | | | | |
| 2 | | | 2 | 2 | 1 | | | |
| 3 | | | | 9 | 9 | | | |
| 4 | | | | | 3 | 3 | 4 | |
| 5 | | | | | | 8 | 7 | 7 |
| 6 | | | | | | | 1 | 5 |
| 7 | | | | | | | | 3 |
С базы на склад в среднем раз в  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
Задана таблица транспортных тарифов.
| A | B | C | D |
| I | 5 | 8 | 6 | 1 |
| II | 2 | 5 | 3 | 1 |
| III | 3 | 4 | 4 | 2 |
| IV | 6 | 1 | 5 | 5 |
| V | 2 | 2 | 2 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
| I | | | | | 80 |
| II | | | | | 55 |
| III | | | | | 110 |
| IV | | | | | 115 |
| V | | | | | 50 |
| Наличие | 60 | 155 | 55 | 140 | 410 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика C к потребителю III (целое число).
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 25 | 20 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 30 |
| II | | | 20 |
| Наличие | 40 | 10 | |
Решить многопродуктовую транспортную задачу.В ответе указать расходы на доставку продукта 2 (целое число).
Найти величину спроса, при котором он равен предложению, если спрос на товар зависит от цены  как
как  , а предложение как
, а предложение как  . Ответ округлить до одного знака после запятой.
. Ответ округлить до одного знака после запятой.
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 25 | 20 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 30 |
| II | | | 20 |
| Наличие | 40 | 10 | |
Решить многопродуктовую транспортную задачу.В ответе указать общее количество груза экспедируемого в направлении A-I (целое число).
Найти максимальный уровень спроса, если спрос на товар зависит от цены  как
как  . Ответ ввести в виде целого числа.
. Ответ ввести в виде целого числа.
С базы на склад в среднем раз в  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве 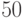 ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 50 |
| II | | | | 130 |
| III | | | | 20 |
| Наличие | 40 | 70 | 90 | 200 |
Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика B к получателю III (целое число).
Задана таблица транспортных тарифов.
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | Потребность |
|---|
| I | | | | 10 |
| II | | | | 35 |
| III | | | | 5 |
| Наличие | 25 | 5 | 20 | 50 |
Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 4 | 9 | 5 | 7 | 100 |
| II | 1 | 3 | 5 | 2 | 40 |
| III | 4 | 7 | 3 | 5 | 60 |
| IV | 6 | 4 | 3 | 5 | 50 |
| Наличие | 80 | 40 | 40 | 90 | 250 |
Создать исходный план перевозок методом северо-западного угла и определить его стоимость.
Найти при каких значениях фиктивных переменных, вводимых в симплекс методе, достигает максимума целевая функция:
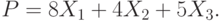
При следующих ограничениях:
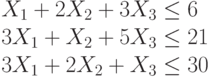
Функция определена только при неотрицательных значениях переменных.
Задана транспортная таблица.
| Потребители | Поставщики | Потребность |
|---|
| I | II | III | IV |
|---|
| I | 4 | 8 | 6 | 7 | 100 |
| II | 1 | 3 | 6 | 2 | 40 |
| III | 4 | 7 | 6 | 5 | 60 |
| IV | 6 | 4 | 3 | 5 | 50 |
| Наличие | 80 | 40 | 40 | 90 | 250 |
Создать исходный план перевозок методом северо-западного угла и определить его стоимость.
Найти цену, при которой спрос равен предложению, если спрос на товар зависит от цены  как
как  , а предложение как
, а предложение как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 3 | 1 | 4 | 1 | 0 | 0 | 10 |
| 0 | 2 | 4 | 6 | 0 | 1 | 0 | 72 |
| 0 | 5 | 7 | 1 | 0 | 0 | 1 | 140 |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 |
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|
| 0 | 4 | 5 | 7 | | | | | | |
| 1 | | | 5 | 5 | | | | | |
| 2 | | | 7 | 3 | 6 | | | | |
| 3 | | | | 6 | 4 | | | | |
| 4 | | | | 1 | 2 | 5 | 8 | | |
| 5 | | | | | | 7 | 2 | 3 | |
| 6 | | | | | | | 5 | 7 | 4 |
| 7 | | | | | | | | 9 | 3 |
| 8 | | | | | | | | | 7 |
Дана матрица левой части системы линейных алгебраических уравнений: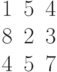 Дан столбец свободных членов:
Дан столбец свободных членов: Найти значение главного определителя системы. Ответ — целое число.
Найти значение главного определителя системы. Ответ — целое число.
Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).
| Состояние | 1 | 2 | 3 | 4 | 5 |
|---|
| 0 | 5 | 3 | 4 | | |
| 1 | | 2 | 2 | 7 | |
| 2 | | | 4 | 6 | 2 |
| 3 | | | | 3 | 5 |
| 4 | | | | | 3 |
С базы на склад в среднем раз в  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве 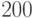 ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
Задана таблица транспортных тарифов.
| A | B | C | D |
|---|
| I | 9 | 2 | 3 | 3 |
| II | 3 | 3 | 4 | 5 |
| III | 5 | 7 | 2 | 6 |
| IV | 7 | 5 | 1 | 3 |
| V | 2 | 4 | 4 | 3 |
Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.
| A | B | C | D | Потребность |
|---|
| I | | | | | 40 |
| II | | | | | 35 |
| III | | | | | 70 |
| IV | | | | | 35 |
| V | | | | | 60 |
| Наличие | 20 | 95 | 50 | 75 | 240 |
Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика A к потребителю I (целое число).
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 25 | 20 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 30 |
| II | | | 20 |
| Наличие | 40 | 10 | |
Решить многопродуктовую транспортную задачу.В ответе указать общее количество груза экспедируемого в направлении B-I (целое число).
Имеются три поставщика  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
Есть данные о наличии и потребности в трех видах продукции.
| Продукт 1 |
| A | B | Потребность |
|---|
| I | | | 20 |
| II | | | 40 |
| Наличие | 10 | 50 | |
| Продукт 2 |
| A | B | Потребность |
|---|
| I | | | 15 |
| II | | | 30 |
| Наличие | 25 | 20 | |
| Продукт 3 |
| A | B | Потребность |
|---|
| I | | | 30 |
| II | | | 20 |
| Наличие | 40 | 10 | |
Решить многопродуктовую транспортную задачу.В ответе указать общие расходы на доставку всех трех продуктов (целое число).
 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением 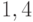 ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа: 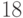 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в 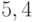 ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  день. Известно, что к началу первого дня остаток на складе составлял
день. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в 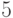 ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  день. Известно, что к началу первого дня остаток на складе составлял
день. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа: 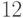 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в 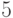 ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве 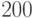 ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением 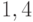 ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет 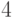 дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа: 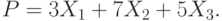
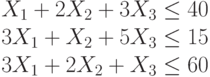
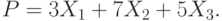

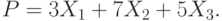

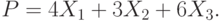

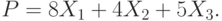
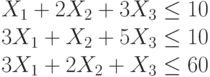
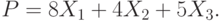

 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве 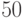 ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением 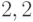 ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа: 







 как
как 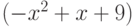 а стоимость хранения как
а стоимость хранения как 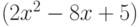 .Ответ округлить до одного знака после запятой.
.Ответ округлить до одного знака после запятой.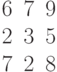 Дан столбец свободных членов:
Дан столбец свободных членов: Найти значение главного определителя системы. Ответ — целое число.
Найти значение главного определителя системы. Ответ — целое число. и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.









 и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.



 и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.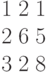 Дан столбец свободных членов:
Дан столбец свободных членов: Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой. как
как  а стоимость хранения как
а стоимость хранения как  .
.





 как
как  , а стоимость хранения как
, а стоимость хранения как  .
.





 как
как  , а предложение как
, а предложение как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.





 как
как  , а предложение как
, а предложение как  . Ответ округлить до одного знака после запятой.
. Ответ округлить до одного знака после запятой.





 как
как  , а предложение как
, а предложение как  . Ответ округлить до одного знака после запятой.
. Ответ округлить до одного знака после запятой.





 как
как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.


 как
как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.


 как
как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.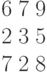 Дан столбец свободных членов:
Дан столбец свободных членов: Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число.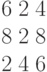 Дан столбец свободных членов:
Дан столбец свободных членов: Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число. Дан столбец свободных членов:
Дан столбец свободных членов: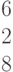 Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число.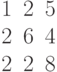 Дан столбец свободных членов:
Дан столбец свободных членов: Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число. Дан столбец свободных членов:
Дан столбец свободных членов: Найти значение главного определителя системы. Ответ -- целое число.
Найти значение главного определителя системы. Ответ -- целое число.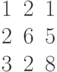 Дан столбец свободных членов:
Дан столбец свободных членов: Найти значение главного определителя системы. Ответ -- целое число.
Найти значение главного определителя системы. Ответ -- целое число. Дан столбец свободных членов:
Дан столбец свободных членов: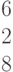 Найти значение главного определителя системы. Ответ -- целое число.
Найти значение главного определителя системы. Ответ -- целое число. Дан столбец свободных членов:
Дан столбец свободных членов: Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.


























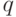
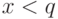 (руб./ед.)
(руб./ед.)
 (руб./ед.)
(руб./ед.)



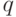
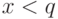 (руб./ед.)
(руб./ед.)
 (руб./ед.)
(руб./ед.)
































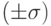 для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

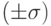 для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

 для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

 для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
 - ремонтных комплектов составляет
- ремонтных комплектов составляет 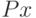 . Аналогично, вероятность того, что в течение дня потребуется
. Аналогично, вероятность того, что в течение дня потребуется  - ремонтных комплектов составляет
- ремонтных комплектов составляет  . При этом, величины
. При этом, величины  и
и  являются случайными с математическими ожиданиями:
являются случайными с математическими ожиданиями:  и
и  и средними квадратичными отклонениями:
и средними квадратичными отклонениями: 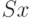 и
и  . Учтите, что при сложении и умножении случайных величин полученная случайная величина имеет среднее квадратичное отклонение, определяемое формулой:
. Учтите, что при сложении и умножении случайных величин полученная случайная величина имеет среднее квадратичное отклонение, определяемое формулой: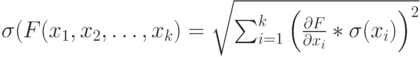 Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за
Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за  дней.
дней.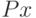




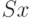

 комплектов.
комплектов.
 - ремонтных комплектов составляет
- ремонтных комплектов составляет 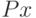 . Аналогично, вероятность того, что в течение дня потребуется
. Аналогично, вероятность того, что в течение дня потребуется  - ремонтных комплектов составляет
- ремонтных комплектов составляет  . При этом, величины
. При этом, величины  и
и  являются случайными с математическими ожиданиями:
являются случайными с математическими ожиданиями:  и
и  и средними квадратичными отклонениями:
и средними квадратичными отклонениями: 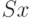 и
и  . Учтите, что при сложении и умножении случайных величин полученная случайная величина имеет среднее квадратичное отклонение, определяемое формулой:
. Учтите, что при сложении и умножении случайных величин полученная случайная величина имеет среднее квадратичное отклонение, определяемое формулой: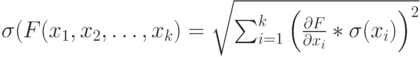 Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за
Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за  дней.
дней.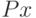




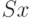

 комплектов.
комплектов.
 и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение среднего
статистические веса.В ответе указать значение среднего  .Ответ округлить до двух знаков после запятой.
.Ответ округлить до двух знаков после запятой.
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение суммы весов.Ответ округлить до двух знаков после запятой.
статистические веса.В ответе указать значение суммы весов.Ответ округлить до двух знаков после запятой.
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение среднего
статистические веса.В ответе указать значение среднего  .Ответ округлить до двух знаков после запятой.
.Ответ округлить до двух знаков после запятой.
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение среднего квадрата
статистические веса.В ответе указать значение среднего квадрата  .Ответ округлить до двух знаков после запятой.
.Ответ округлить до двух знаков после запятой.
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение среднего
статистические веса.В ответе указать значение среднего  .Ответ округлить до двух знаков после запятой.
.Ответ округлить до двух знаков после запятой.
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение среднего произведения
статистические веса.В ответе указать значение среднего произведения 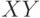 .Ответ округлить до двух знаков после запятой.
.Ответ округлить до двух знаков после запятой.
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение
статистические веса.В ответе указать значение  .Ответ округлить до одного знака после запятой.
.Ответ округлить до одного знака после запятой.
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение
статистические веса.В ответе указать значение  .Ответ округлить до двух знаков после запятой.
.Ответ округлить до двух знаков после запятой.
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение остаточного среднего квадратичного отклонения определяемого по формуле:
статистические веса.В ответе указать значение остаточного среднего квадратичного отклонения определяемого по формуле: ![\sigma_{ост}=\frac{\sum_{i=1}^n[(y_i-kx_i-b)^2w_i]}{\sum_[i=1}^nw_i}](https://intuit.ru//sites/default/files/tex_cache/56b4a0ebe2e9a6b88e0dda66e55672a7.png) .Ответ округлить до трех знаков после запятой.
.Ответ округлить до трех знаков после запятой.
 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.













 и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где 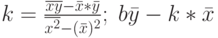 . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение остаточного среднего квадратичного отклонения определяемого по формуле:
статистические веса.В ответе указать значение остаточного среднего квадратичного отклонения определяемого по формуле: ![\sigma_{ост}=\frac{\sum_{i=1}^n[(y_i-kx_i-b)^2w_i]}{\sum_[i=1}^nw_i}](https://intuit.ru//sites/default/files/tex_cache/56b4a0ebe2e9a6b88e0dda66e55672a7.png) .Ответ округлить до трех знаков после запятой.
.Ответ округлить до трех знаков после запятой.
 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение среднего
статистические веса.В ответе указать значение среднего  .Ответ округлить до трех знаков после запятой.
.Ответ округлить до трех знаков после запятой.





 как
как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.


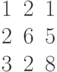 Дан столбец свободных членов:
Дан столбец свободных членов: Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число. наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение
статистические веса.В ответе указать значение  .Ответ округлить до двух знаков после запятой.
.Ответ округлить до двух знаков после запятой.
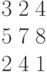 Дан столбец свободных членов:
Дан столбец свободных членов: Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число. и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.
 как
как  , а стоимость хранения как
, а стоимость хранения как  .
.





 - ремонтных комплектов составляет
- ремонтных комплектов составляет 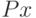 . Аналогично, вероятность того, что в течение дня потребуется
. Аналогично, вероятность того, что в течение дня потребуется  - ремонтных комплектов составляет
- ремонтных комплектов составляет  . При этом, величины
. При этом, величины  и
и  являются случайными с математическими ожиданиями:
являются случайными с математическими ожиданиями:  и
и  и средними квадратичными отклонениями:
и средними квадратичными отклонениями: 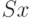 и
и  . Учтите, что при сложении и умножении случайных величин полученная случайная величина имеет среднее квадратичное отклонение, определяемое формулой:
. Учтите, что при сложении и умножении случайных величин полученная случайная величина имеет среднее квадратичное отклонение, определяемое формулой: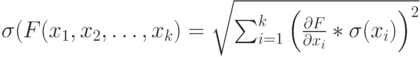 Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за
Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за  дней.
дней.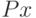




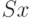

 комплектов.
комплектов.
 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа: 








 как
как  , а предложение как
, а предложение как  . Ответ округлить до одного знака после запятой.
. Ответ округлить до одного знака после запятой.





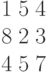 Дан столбец свободных членов:
Дан столбец свободных членов: Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число.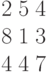 Дан столбец свободных членов:
Дан столбец свободных членов: Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число. Дан столбец свободных членов:
Дан столбец свободных членов: Найти значение главного определителя системы. Ответ — целое число.
Найти значение главного определителя системы. Ответ — целое число.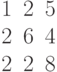 Дан столбец свободных членов:
Дан столбец свободных членов: Найти значение главного определителя системы. Ответ -- целое число.
Найти значение главного определителя системы. Ответ -- целое число.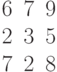 Дан столбец свободных членов:
Дан столбец свободных членов: Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.







































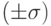 для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

 для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
 - ремонтных комплектов составляет
- ремонтных комплектов составляет 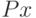 . Аналогично, вероятность того, что в течение дня потребуется
. Аналогично, вероятность того, что в течение дня потребуется  - ремонтных комплектов составляет
- ремонтных комплектов составляет  . При этом, величины
. При этом, величины  и
и  являются случайными с математическими ожиданиями:
являются случайными с математическими ожиданиями:  и
и  и средними квадратичными отклонениями:
и средними квадратичными отклонениями: 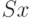 и
и  . Учтите, что при сложении и умножении случайных величин полученная случайная величина имеет среднее квадратичное отклонение, определяемое формулой:
. Учтите, что при сложении и умножении случайных величин полученная случайная величина имеет среднее квадратичное отклонение, определяемое формулой: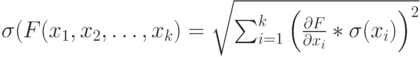 Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за
Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за  дней.
дней.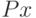




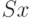

 комплектов.
комплектов.
 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в 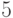 ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением 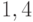 ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.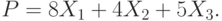
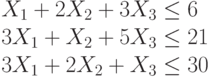
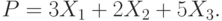

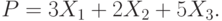
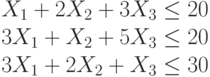
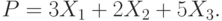
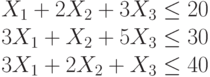
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение среднего X.Ответ округлить до одного знака после запятой.
статистические веса.В ответе указать значение среднего X.Ответ округлить до одного знака после запятой.
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение суммы весов.Ответ округлить до трех знаков после запятой.
статистические веса.В ответе указать значение суммы весов.Ответ округлить до трех знаков после запятой.
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение среднего произведения
статистические веса.В ответе указать значение среднего произведения  .Ответ округлить до двух знаков после запятой.
.Ответ округлить до двух знаков после запятой.
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение
статистические веса.В ответе указать значение  .Ответ записать с точностью до двух знаков после запятой.
.Ответ записать с точностью до двух знаков после запятой.
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение остаточного среднего квадратичного отклонения определяемого по формуле:
статистические веса.В ответе указать значение остаточного среднего квадратичного отклонения определяемого по формуле: ![\sigma_{ост}=\frac{\sum_{i=1}^n[(y_i-kx_i-b)^2w_i]}{\sum_[i=1}^nw_i}](https://intuit.ru//sites/default/files/tex_cache/56b4a0ebe2e9a6b88e0dda66e55672a7.png) .Ответ округлить до двух знаков после запятой.
.Ответ округлить до двух знаков после запятой.
 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением 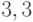 ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  день. Известно, что к началу первого дня остаток на складе составлял
день. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа: 
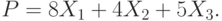
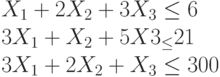


 для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
 как
как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.


 и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение среднего квадрата
статистические веса.В ответе указать значение среднего квадрата  .Ответ округлить до двух знаков после запятой.
.Ответ округлить до двух знаков после запятой.





 для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
 как
как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.


 как
как  , а предложение как
, а предложение как  . Ответ округлить до одного знака после запятой.
. Ответ округлить до одного знака после запятой.





 как
как  . Ответ округлить до одного знака после запятой.
. Ответ округлить до одного знака после запятой.


 как
как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.


 Дан столбец свободных членов:
Дан столбец свободных членов: Найти сумму корней системы. Ответ -- целое число.
Найти сумму корней системы. Ответ -- целое число.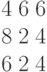 Дан столбец свободных членов:
Дан столбец свободных членов: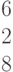 Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.










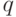
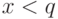 (руб./ед.)
(руб./ед.)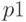
 (руб./ед.)
(руб./ед.)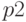


















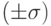 для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

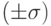 для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

 для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
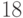 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве 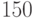 ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в 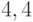 ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением 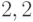 ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.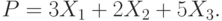

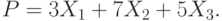
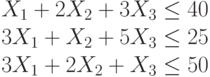
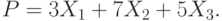
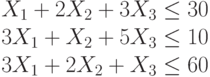
 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.








 и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




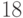 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве 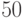 ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в 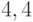 ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  день. Известно, что к началу первого дня остаток на складе составлял
день. Известно, что к началу первого дня остаток на складе составлял 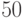 ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.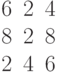 Дан столбец свободных членов:
Дан столбец свободных членов: Найти значение главного определителя системы. Ответ -- целое число.
Найти значение главного определителя системы. Ответ -- целое число. и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.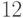 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в 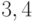 ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа: 
 для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.
 как
как  а стоимость хранения как
а стоимость хранения как  .
.





 как
как  , а стоимость хранения как
, а стоимость хранения как  .
.





 как
как  , а предложение как
, а предложение как  . Ответ округлить до одного знака после запятой.
. Ответ округлить до одного знака после запятой.





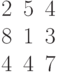 Дан столбец свободных членов:
Дан столбец свободных членов: Найти значение главного определителя системы. Ответ -- целое число.
Найти значение главного определителя системы. Ответ -- целое число.














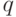
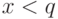 (руб./ед.)
(руб./ед.)
 (руб./ед.)
(руб./ед.)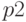

 - ремонтных комплектов составляет
- ремонтных комплектов составляет 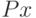 . Аналогично, вероятность того, что в течение дня потребуется
. Аналогично, вероятность того, что в течение дня потребуется  - ремонтных комплектов составляет
- ремонтных комплектов составляет  . При этом, величины
. При этом, величины  и
и  являются случайными с математическими ожиданиями:
являются случайными с математическими ожиданиями:  и
и  и средними квадратичными отклонениями:
и средними квадратичными отклонениями: 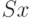 и
и  . Учтите, что при сложении и умножении случайных величин полученная случайная величина имеет среднее квадратичное отклонение, определяемое формулой:
. Учтите, что при сложении и умножении случайных величин полученная случайная величина имеет среднее квадратичное отклонение, определяемое формулой: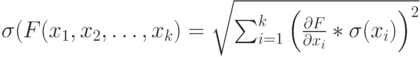 Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за
Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за  дней.
дней.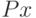




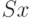

 комплектов.
комплектов.
 - ремонтных комплектов составляет
- ремонтных комплектов составляет 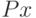 . Аналогично, вероятность того, что в течение дня потребуется
. Аналогично, вероятность того, что в течение дня потребуется  - ремонтных комплектов составляет
- ремонтных комплектов составляет  . При этом, величины
. При этом, величины  и
и  являются случайными с математическими ожиданиями:
являются случайными с математическими ожиданиями:  и
и  и средними квадратичными отклонениями:
и средними квадратичными отклонениями: 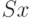 и
и  . Учтите, что при сложении и умножении случайных величин полученная случайная величина имеет среднее квадратичное отклонение, определяемое формулой:
. Учтите, что при сложении и умножении случайных величин полученная случайная величина имеет среднее квадратичное отклонение, определяемое формулой: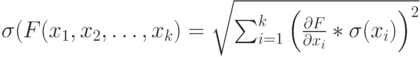 Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за
Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за  дней.
дней.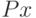




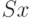

 комплектов.
комплектов.
 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве 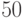 ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением 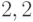 ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:  дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:  и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение суммы весов.Ответ округлить до двух знаков после запятой.
статистические веса.В ответе указать значение суммы весов.Ответ округлить до двух знаков после запятой.
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение среднего квадрата
статистические веса.В ответе указать значение среднего квадрата  .Ответ округлить до двух знаков после запятой.
.Ответ округлить до двух знаков после запятой.
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение среднего произведения
статистические веса.В ответе указать значение среднего произведения 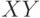 .Ответ округлить до двух знаков после запятой.
.Ответ округлить до двух знаков после запятой.
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение
статистические веса.В ответе указать значение  .Ответ записать с точностью до двух знаков после запятой.
.Ответ записать с точностью до двух знаков после запятой.







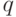
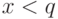 (руб./ед.)
(руб./ед.)
 (руб./ед.)
(руб./ед.)




 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где 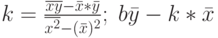 . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение остаточного среднего квадратичного отклонения определяемого по формуле:
статистические веса.В ответе указать значение остаточного среднего квадратичного отклонения определяемого по формуле: ![\sigma_{ост}=\frac{\sum_{i=1}^n[(y_i-kx_i-b)^2w_i]}{\sum_[i=1}^nw_i}](https://intuit.ru//sites/default/files/tex_cache/56b4a0ebe2e9a6b88e0dda66e55672a7.png) .Ответ округлить до двух знаков после запятой.
.Ответ округлить до двух знаков после запятой.
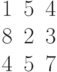 Дан столбец свободных членов:
Дан столбец свободных членов: Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.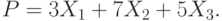
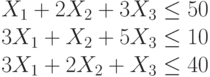
 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 как
как 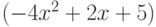 , а предложение как
, а предложение как 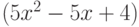 . Ответ округлить до одного знака после запятой.
. Ответ округлить до одного знака после запятой. Дан столбец свободных членов:
Дан столбец свободных членов: Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.
Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.







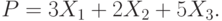

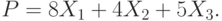
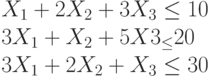
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение
статистические веса.В ответе указать значение  .Ответ округлить до двух знаков после запятой.
.Ответ округлить до двух знаков после запятой.
 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение остаточного среднего квадратичного отклонения определяемого по формуле:
статистические веса.В ответе указать значение остаточного среднего квадратичного отклонения определяемого по формуле: ![\sigma_{ост}=\frac{\sum_{i=1}^n[(y_i-kx_i-b)^2w_i]}{\sum_[i=1}^nw_i}](https://intuit.ru//sites/default/files/tex_cache/56b4a0ebe2e9a6b88e0dda66e55672a7.png) .Ответ округлить до двух знаков после запятой.
.Ответ округлить до двух знаков после запятой.
 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:  наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где 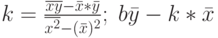 . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение остаточного среднего квадратичного отклонения определяемого по формуле:
статистические веса.В ответе указать значение остаточного среднего квадратичного отклонения определяемого по формуле: ![\sigma_{ост}=\frac{\sum_{i=1}^n[(y_i-kx_i-b)^2w_i]}{\sum_[i=1}^nw_i}](https://intuit.ru//sites/default/files/tex_cache/56b4a0ebe2e9a6b88e0dda66e55672a7.png) .Ответ округлить до двух знаков после запятой.
.Ответ округлить до двух знаков после запятой.
 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. как
как  , а предложение как
, а предложение как  . Ответ округлить до одного знака после запятой.
. Ответ округлить до одного знака после запятой.





 и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. как
как  . Ответ ввести в виде целого числа.
. Ответ ввести в виде целого числа.


 дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа: 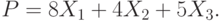
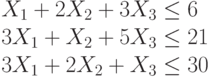
 как
как  , а предложение как
, а предложение как  . Ответ округлить до двух знаков после запятой.
. Ответ округлить до двух знаков после запятой.








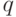
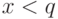 (руб./ед.)
(руб./ед.)
 (руб./ед.)
(руб./ед.)




 наборов (
наборов ( ) значений двух переменных:
) значений двух переменных:  (уровень сервисного обслуживания) и
(уровень сервисного обслуживания) и  (уровень целевого параметра - экономический эффект). Величина
(уровень целевого параметра - экономический эффект). Величина  - это оценочное значение, полученное с погрешностью
- это оценочное значение, полученное с погрешностью  .
.


 , где
, где  . Для вычисления средних значений используются формулы:
. Для вычисления средних значений используются формулы: Здесь
Здесь  статистические веса.В ответе указать значение среднего
статистические веса.В ответе указать значение среднего  .Ответ округлить до одного знака после запятой.
.Ответ округлить до одного знака после запятой.
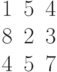 Дан столбец свободных членов:
Дан столбец свободных членов: Найти значение главного определителя системы. Ответ — целое число.
Найти значение главного определителя системы. Ответ — целое число. дней поставляют апельсины в количестве
дней поставляют апельсины в количестве  ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в
ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в  ящиков апельсинов в день, со средним квадратичным отклонением
ящиков апельсинов в день, со средним квадратичным отклонением  ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет
ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет  дня. Известно, что к началу первого дня остаток на складе составлял
дня. Известно, что к началу первого дня остаток на складе составлял  ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:
ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа: 



 , где
, где  -цена. Предложение зависит от цены
-цена. Предложение зависит от цены  следующим образом:
следующим образом:  . При изменении баланса спроса и предложения цена изменяется в соответствии с законом:
. При изменении баланса спроса и предложения цена изменяется в соответствии с законом:  . Решение этого дифференциально уравнения имеет вид:
. Решение этого дифференциально уравнения имеет вид:  ; где
; где  - цена до изменения баланса спроса и предложения.
- цена до изменения баланса спроса и предложения.




 и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов. и три потребителя
и три потребителя  . Задана матрица транспортных тарифов.
. Задана матрица транспортных тарифов.