База ответов ИНТУИТ

Математический анализ - 1

<<- Назад к вопросам

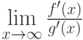Пусть f и g - бесконечно малые на бесконечности функции, для которых существует предел \lim\limits_{x \to \infty} {\frac {f'(x)} {g'(x)}}. Тогда существует предел

(Отметьте один правильный вариант ответа.)
Варианты ответа
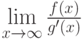
\lim\limits_{x \to \infty} {\frac {f(x)} {g'(x)}}
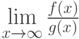\lim\limits_{x \to \infty} {\frac {f(x)} {g(x)}}(Верный ответ)
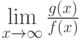
\lim\limits_{x \to \infty} {\frac {g(x)} {f(x)}}
\lim\limits_{x \to \infty} {\frac {g(x)} {f'(x)}}
Похожие вопросы
Пусть f и g - бесконечно большие на бесконечности функции, для которых существует предел \lim\limits_{x \to \infty} {\frac {f'(x)} {g'(x)}}. Тогда существует предел
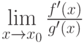Пусть f и g - бесконечно малые в точке x_0 функции, для которых существует предел \lim\limits_{x \to x_0} {\frac {f'(x)} {g'(x)}}. Тогда существует предел
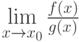
Пусть f и g - бесконечно большие в точке x_0 функции, для которых существует предел \lim\limits_{x \to x_0} {\frac {f'(x)} {g'(x)}}. Тогда существует предел
Пусть выполнены условия теоремы 6 (правило Лопиталя) для бесконечно больших функций f и g на бесконечности. Тогда предел \lim\limits_{x \to \infty} {\frac {f(x)} {g(x)}}
Пусть выполнены условия теоремы 4 (правило Лопиталя) для бесконечно малых функций f и g. Тогда предел \lim\limits_{x \to x_0} {\frac {f(x)} {g(x)}}
Пусть выполнены условия теоремы 5 (правило Лопиталя) для бесконечно больших функций f и g. Тогда предел \lim\limits_{x \to x_0} {\frac {f(x)} {g(x)}}
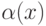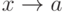Пусть f(x) определена в некоторой окрестности точки a и \lim\limits_{x \to a} {f(x)} = A + \alpha (x). Тогда (\alpha (x) - б.м.ф. при x \to a). Тогда предел функции f(x)
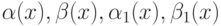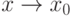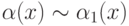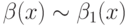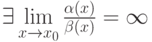Пусть \alpha (x), \beta (x), \alpha_1 (x), \beta_1 (x) - бесконечно малые при x \to x_0 функции, причём \alpha (x) \sim \alpha_1 (x) и \beta (x) \sim \beta_1 (x). Если \exists \lim\limits_{x \to x_0} {\frac {\alpha (x)} {\beta (x)}} = \infty, то
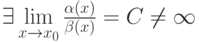Пусть \alpha (x), \beta (x), \alpha_1 (x), \beta_1 (x) - бесконечно малые при x \to x_0 функции, причём \alpha (x) \sim \alpha_1 (x) и \beta (x) \sim \beta_1 (x). Если \exists \lim\limits_{x \to x_0} {\frac {\alpha (x)} {\beta (x)}} = C \neq \infty, то
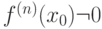Пусть для функции f(x) в окрестности точки x_0 существует производная n-го порядка и f^{(n)}(x_0) \neg 0 - первая отличная от нуля производная. Тогда 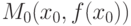M_0(x_0,f(x_0)) является точкой перегиба графика функции, если