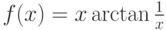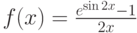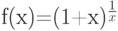Если функция  непрерывна в точке
непрерывна в точке  , а функция
, а функция  непрерывна в точке
непрерывна в точке  , то сложная функция
, то сложная функция ![y = f[\varphi (x)]](https://intuit.ru//sites/default/files/tex_cache/ead719ea19850ef1759fce07ef02772d.png)
(Отметьте один правильный вариант ответа.)
Варианты ответа
непрерывна в точке  (Верный ответ)
(Верный ответ)
 (Верный ответ)
(Верный ответ)
разрывна в точке 

![\exists \lim\limits_{x \to x_0} {f[\varphi (x)]} \neq f[\varphi (x)]](https://intuit.ru//sites/default/files/tex_cache/7b0ae68f8e232aa373e31f9a0742fcf9.png)

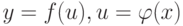 в точках
в точках 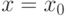 соответственно , чтобы сложная функция
соответственно , чтобы сложная функция  , но
, но  при переходе через точку
при переходе через точку  задана параметрически:
задана параметрически: 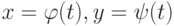 . Каким условиям должна удовлетворять функция
. Каким условиям должна удовлетворять функция 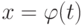 на интервале
на интервале 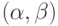 для того, чтобы существовала производная
для того, чтобы существовала производная 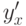 :
: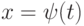 на интервале
на интервале ![\left[x\right]](https://intuit.ru//sites/default/files/tex_cache/fed5f6dcdaa57752ef9a484febad21d3.png) - целая часть от
- целая часть от  .
. 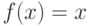 если
если  и
и 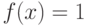 , если
, если 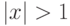
 так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение  .
.