Пусть задан ряд 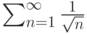 . Тогда
. Тогда
(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
предел последовательности частичных сумм ряда не существует
предел 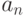 при
при 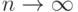 равен нулю(Верный ответ)
равен нулю(Верный ответ)
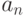 при
при 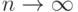 равен нулю(Верный ответ)
равен нулю(Верный ответ)
ряд расходится(Верный ответ)
последовательность частичных сумм ряда сходится
сумма ряда конечна

 . Тогда он
. Тогда он  . Тогда он
. Тогда он ![\sum_{n=1}^\infty (-1)^{n+1} \frac{1}{\sqrt[3]{n}}](https://intuit.ru//sites/default/files/tex_cache/8372d05679431edaccd76ee8b5f79056.png) . Тогда он
. Тогда он 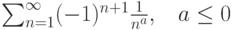 . Тогда он
. Тогда он  . Тогда он
. Тогда он 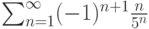 . Тогда он
. Тогда он  . Тогда он
. Тогда он 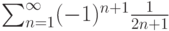 . Тогда он
. Тогда он 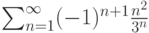 . Тогда он
. Тогда он 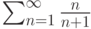 . Тогда
. Тогда