Математический анализ. Ряды - ответы
Количество вопросов - 152
Пусть задан ряд  . Тогда он
. Тогда он
Пусть функция  - аналитическая в точке
- аналитическая в точке  . Тогда
. Тогда
Пусть ряд 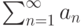 с положительными членами расходится. Какие условия должны выполняться:
с положительными членами расходится. Какие условия должны выполняться:
Пусть задана неотрицательная  при
при  , числовой ряд
, числовой ряд 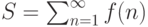 и несобственный интеграл
и несобственный интеграл  .Отметьте верные утверждения:
.Отметьте верные утверждения:
Отметьте верные утверждения:
Отметьте верные утверждения:
Пусть задан ряд  . Тогда он
. Тогда он
Отметьте все сходящиеся ряды:
Пусть задан ряд с неотрицательными членами. Отметьте верные утверждения:
Функциональный ряд  сходится равномерно к сумме ряда
сходится равномерно к сумме ряда  -функциональная последовательность частичных сумм ряда, если
-функциональная последовательность частичных сумм ряда, если
Пусть задан ряд 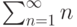 . Тогда
. Тогда
Рассмотрим интеграл 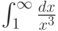 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Рассмотрим несобственные интегралы 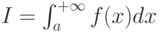 и
и 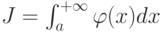 от неотрицательных функций, для которых существует конечный предел
от неотрицательных функций, для которых существует конечный предел 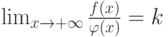 Отметьте верные утверждения:
Отметьте верные утверждения:
Отметьте верные утверждения:
Отметьте верные утверждения:
Пусть задан степенной ряд 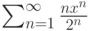 . Найдите радиус сходимости ряда.
. Найдите радиус сходимости ряда.
Отметьте верные утверждения:
Какие условия являются необходимыми для сходимости ряд Тейлора бесконечно дифференцируемой функции  к этой функции:
к этой функции:
Отметьте верные утверждения:
Какой должна быть функция сравнения 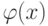 при исследовании на сходимость интеграла
при исследовании на сходимость интеграла 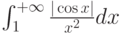 :
:
Пусть задан ряд 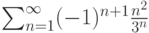 . Тогда он
. Тогда он
Какие условия на функции 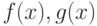 (признак Дирихле) при
(признак Дирихле) при  должны выполняться для сходимости интеграла
должны выполняться для сходимости интеграла 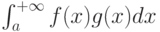 :
:
Пусть заданы ряды (1) 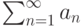 и (2)
и (2) 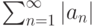 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Несобственный интеграл 1 рода сходится, если предел функции 
Пусть задан ряд 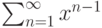 . Тогда
. Тогда
Отметьте все расходящиеся интегралы:
Отметьте верные утверждения:
Отметьте верные утверждения:
Число 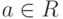 не является пределом последовательности
не является пределом последовательности  ,если
,если
Отметьте верные утверждения:
Пусть задан ряд 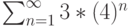 . Тогда
. Тогда
Пусть задан ряд 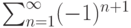 . Тогда
. Тогда
Отметьте верные утверждения:
Отметьте верные утверждения:
Пусть задан ряд с неотрицательными членами. Отметьте верные утверждения:
Пусть ряд 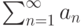 с положительными членами сходится. Какие условия должны выполняться:
с положительными членами сходится. Какие условия должны выполняться:
Пусть ряд 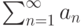 с положительными членами расходится. Какие условия должны выполняться:
с положительными членами расходится. Какие условия должны выполняться:
Несобственный интеграл 1 рода сходится, если предел функции 
Рассмотрим интеграл 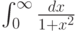 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Отметьте верные утверждения:
Рассмотрим несобственные интегралы 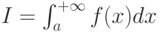 и
и 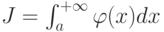 для функций, связанных неравенством
для функций, связанных неравенством  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Какой должна быть функция сравнения 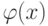 при исследовании на сходимость интеграла
при исследовании на сходимость интеграла 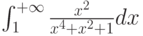 :
:
Какие условия на функции 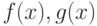 (признак Дирихле) при
(признак Дирихле) при  должны выполняться для сходимости интеграла
должны выполняться для сходимости интеграла 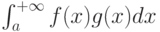 :
:
Пусть задана  , числовой ряд
, числовой ряд 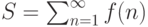 и несобственный интеграл
и несобственный интеграл  . Какие условия на функцию
. Какие условия на функцию  должны выполняться для равносильности сходимости ряда и интеграла.:
должны выполняться для равносильности сходимости ряда и интеграла.:
Отметьте все сходящиеся интегралы:
Пусть задан ряд  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Пусть неотрицательный ряд 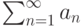 сходится. Какие условия являются признаками сходимости:
сходится. Какие условия являются признаками сходимости:
Отметьте верные утверждения:
Пусть заданы ряды (1) 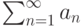 и (2)
и (2) 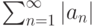 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Пусть задан ряд 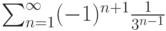 . Тогда он
. Тогда он
Пусть задан ряд ![\sum_{n=1}^\infty (-1)^{n+1} \frac{1}{\sqrt[3]{n}}](https://intuit.ru//sites/default/files/tex_cache/8372d05679431edaccd76ee8b5f79056.png) . Тогда он
. Тогда он
Пусть задан ряд 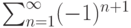 . Тогда он
. Тогда он
Отметьте верные утверждения:
Функциональная последовательность  не сходится равномерно к своей предельной функции, если
не сходится равномерно к своей предельной функции, если
Какие условия входят в список достаточных для равномерной сходимости функциональной последовательности  :
:
Пусть задан ряд 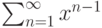 . Тогда он сходится равномерно на множестве
. Тогда он сходится равномерно на множестве
Какие условия входят в признак Вейерштрасса равномерной сходимости функционального ряда:
Отметьте верные утверждения:
Отметьте условия, входящие в число достаточных для дифференцирования функционального ряда:
Пусть задан степенной ряд 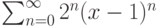 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Пусть задан степенной ряд 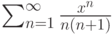 . Найдите радиус сходимости ряда.
. Найдите радиус сходимости ряда.
Какие условия являются достаточными для сходимости ряд Тейлора бесконечно дифференцируемой функции  к этой функции:
к этой функции:
Пусть задана функция 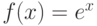 . Тогда
. Тогда
Пусть задана функция 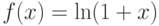 . Тогда
. Тогда
Пусть задана функция  . Тогда
. Тогда
Отметьте верные утверждения:
Рассмотрим несобственные интегралы 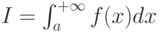 и
и 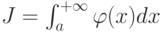 от неотрицательных функций, для которых существует конечный предел
от неотрицательных функций, для которых существует конечный предел 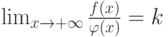 Отметьте верные утверждения:
Отметьте верные утверждения:
Какие условия входят в признак Вейерштрасса равномерной сходимости функционального ряда:
Пусть неотрицательный ряд 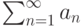 сходится. Какие условия являются признаками сходимости:
сходится. Какие условия являются признаками сходимости:
Пусть задан ряд  . Тогда он
. Тогда он
Пусть задан ряд 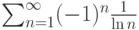 . Тогда он
. Тогда он
Рассмотрим интеграл 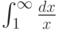 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Пусть ряд 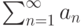 с положительными членами сходится. Какие условия должны выполняться:
с положительными членами сходится. Какие условия должны выполняться:
Отметьте условия, входящие в число достаточных для дифференцирования функционального ряда:
Пусть задан степенной ряд 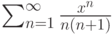 . Отметьте верные утверждения:
. Отметьте верные утверждения:
Вычислите интеграл  . Ответ разделите на
. Ответ разделите на  .
.
Пусть 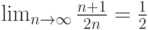 . Определить номер, начиная с которого выполняется неравенство
. Определить номер, начиная с которого выполняется неравенство 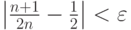 , если
, если 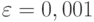 .
.
Вычислить сумму ряда  .
.
Вычислить сумму ряда 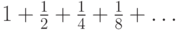 .
.
Вычислите интеграл  . Ответ умножьте на
. Ответ умножьте на 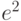 .
.
Найдите сумму ряда  и вычислите её значение в точке
и вычислите её значение в точке  .
.
Вычислить сумму ряда  .
.
Какие условия входят в список достаточных для равномерной сходимости функциональной последовательности  :
:
Вычислите интеграл 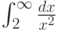 .
.
Пусть задан ряд  . Тогда он
. Тогда он
Отметьте верные утверждения:
Пусть функция  - аналитическая в точке
- аналитическая в точке  . Тогда
. Тогда
Отметьте верные утверждения:
Отметьте верные утверждения:
Найдите сумму ряда  и вычислите её значение в точке
и вычислите её значение в точке 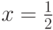 .
.
Пусть задана  , числовой ряд
, числовой ряд 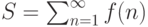 и несобственный интеграл
и несобственный интеграл  . Какие условия на функцию
. Какие условия на функцию  должны выполняться для равносильности сходимости ряда и интеграла.:
должны выполняться для равносильности сходимости ряда и интеграла.:
Отметьте все расходящиеся ряды:
Какой должна быть функция сравнения 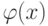 при исследовании на сходимость интеграла
при исследовании на сходимость интеграла 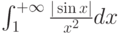 :
:
Отметьте верные утверждения:
Пусть задан ряд 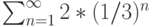 . Тогда
. Тогда
Пусть задан степенной ряд  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Рассмотрим интеграл  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Пусть 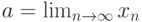 . Тогда вне каждой окрестности
. Тогда вне каждой окрестности 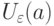 -
-
Пусть числовая последовательность 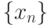 сходится. Отметьте верные утверждения:
сходится. Отметьте верные утверждения:
Вычислить предел последовательности 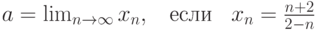 , если.
, если.
Вычислить сумму ряда 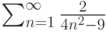 .
.
Отметьте верные утверждения:
Отметьте верные утверждения:
Пусть задан ряд с неотрицательными членами. Отметьте верные утверждения:
Рассмотрим несобственные интегралы 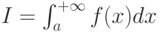 и
и 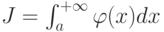 для функций, связанных неравенством
для функций, связанных неравенством  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Какой должна быть функция сравнения 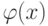 при исследовании на сходимость интеграла
при исследовании на сходимость интеграла 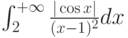 :
:
Рассмотрим несобственные интегралы 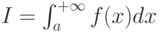 и
и 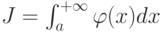 от неотрицательных функций, для которых существует конечный предел
от неотрицательных функций, для которых существует конечный предел 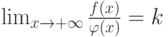 Отметьте верные утверждения:
Отметьте верные утверждения:
Какой должна быть функция сравнения 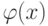 при исследовании на сходимость интеграла
при исследовании на сходимость интеграла 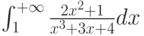 :
:
Пусть задан ряд  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Пусть задан ряд 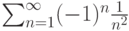 . Тогда он
. Тогда он
Пусть задан ряд  . Тогда он
. Тогда он
Функциональная последовательность  сходится равномерно к своей предельной функции, если
сходится равномерно к своей предельной функции, если
Найдите сумму ряда 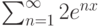 , вычислите её значение в точке
, вычислите её значение в точке 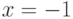 и ответ умножьте на
и ответ умножьте на  .
.
Отметьте условия, входящие в число достаточных для дифференцирования функционального ряда:
Пусть задана функция  . Тогда
. Тогда
Пусть 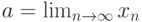 . Тогда внутри каждой окрестности
. Тогда внутри каждой окрестности 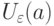 -
-
Пусть неотрицательный ряд 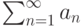 расходится. Какие условия являются признаками расходимости:
расходится. Какие условия являются признаками расходимости:
Пусть задан степенной ряд  . Найдите радиус сходимости ряда.
. Найдите радиус сходимости ряда.
Пусть задана функция  . Тогда
. Тогда
Какие условия на функции 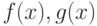 (признак Дирихле) при
(признак Дирихле) при  должны выполняться для сходимости интеграла
должны выполняться для сходимости интеграла 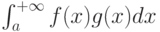 :
:
Пусть задан ряд  . Тогда он
. Тогда он
Какой должна быть функция сравнения 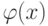 при исследовании на сходимость интеграла
при исследовании на сходимость интеграла ![\int_1^{+\infty} \frac{dx}{\sqrt[3]{x^2+1}}](https://intuit.ru//sites/default/files/tex_cache/ab398964f038db99fc8d0db8cbd35f42.png) :
:
Пусть задан ряд 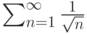 . Тогда
. Тогда
Пусть задан ряд 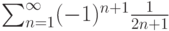 . Тогда он
. Тогда он
Пусть задан ряд  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Отметьте верные утверждения:
Отметьте верные утверждения:
Пусть  . Определить номер, начиная с которого выполняется неравенство
. Определить номер, начиная с которого выполняется неравенство  , если
, если 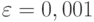 .
.
Пусть ряд 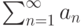 с положительными членами сходится. Какие условия должны выполняться:
с положительными членами сходится. Какие условия должны выполняться:
Пусть задан ряд 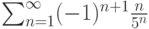 . Тогда он
. Тогда он
Пусть задан ряд 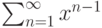 . Тогда
. Тогда
Какие условия являются критерием того, что функциональный ряд не является равномерно сходящимся:
Отметьте верные утверждения:
Отметьте верные утверждения:
Вычислите интеграл 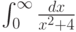 . Ответ разделите на
. Ответ разделите на  .
.
Пусть ряд 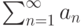 с положительными членами расходится. Какие условия должны выполняться:
с положительными членами расходится. Какие условия должны выполняться:
Пусть задан ряд 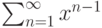 . Тогда
. Тогда
Пусть задана неотрицательная  при
при  , числовой ряд
, числовой ряд 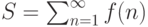 и несобственный интеграл
и несобственный интеграл  .Отметьте верные утверждения:
.Отметьте верные утверждения:
Пусть задан ряд 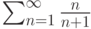 . Тогда
. Тогда
Отметьте верные утверждения:
Рассмотрим несобственные интегралы 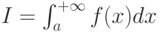 и
и 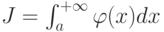 для функций, связанных неравенством
для функций, связанных неравенством  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Вычислите интеграл 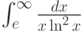 .
.
Найдите сумму ряда 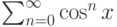 и вычислите её значение в точке
и вычислите её значение в точке  .
.
Отметьте верные утверждения:
Пусть задана функция  . Тогда
. Тогда
Пусть задан ряд 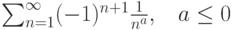 . Тогда он
. Тогда он
Какие условия являются критерием Коши равномерной сходимости ряда:
Пусть задан ряд  . Тогда он
. Тогда он
Вычислить сумму ряда  .
.
Пусть задан ряд  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Число 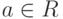 является пределом последовательности
является пределом последовательности 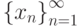 ,если
,если
Вычислить предел последовательности 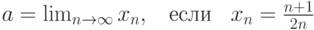 , если.
, если.

 при
при  , числовой ряд
, числовой ряд 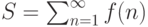 и несобственный интеграл
и несобственный интеграл  .Отметьте верные утверждения:
.Отметьте верные утверждения: сходится равномерно к сумме ряда
сходится равномерно к сумме ряда  -функциональная последовательность частичных сумм ряда, если
-функциональная последовательность частичных сумм ряда, если 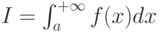 и
и 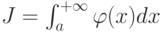 от неотрицательных функций, для которых существует конечный предел
от неотрицательных функций, для которых существует конечный предел 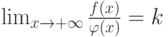 Отметьте верные утверждения:
Отметьте верные утверждения: к этой функции:
к этой функции: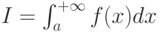 и
и 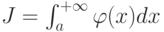 для функций, связанных неравенством
для функций, связанных неравенством  . Отметьте верные утверждения:
. Отметьте верные утверждения: , числовой ряд
, числовой ряд 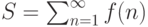 и несобственный интеграл
и несобственный интеграл  . Какие условия на функцию
. Какие условия на функцию  должны выполняться для равносильности сходимости ряда и интеграла.:
должны выполняться для равносильности сходимости ряда и интеграла.: :
: к этой функции:
к этой функции: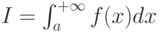 и
и 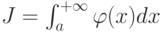 от неотрицательных функций, для которых существует конечный предел
от неотрицательных функций, для которых существует конечный предел 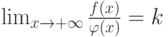 Отметьте верные утверждения:
Отметьте верные утверждения: :
: , числовой ряд
, числовой ряд 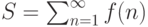 и несобственный интеграл
и несобственный интеграл  . Какие условия на функцию
. Какие условия на функцию  должны выполняться для равносильности сходимости ряда и интеграла.:
должны выполняться для равносильности сходимости ряда и интеграла.: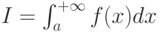 и
и 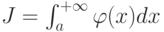 для функций, связанных неравенством
для функций, связанных неравенством  . Отметьте верные утверждения:
. Отметьте верные утверждения: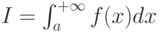 и
и 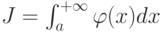 от неотрицательных функций, для которых существует конечный предел
от неотрицательных функций, для которых существует конечный предел 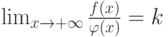 Отметьте верные утверждения:
Отметьте верные утверждения: при
при  , числовой ряд
, числовой ряд 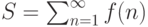 и несобственный интеграл
и несобственный интеграл  .Отметьте верные утверждения:
.Отметьте верные утверждения: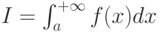 и
и 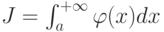 для функций, связанных неравенством
для функций, связанных неравенством  . Отметьте верные утверждения:
. Отметьте верные утверждения: