Вектор показателей 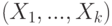 требуется наилучшим образом описать вектором общих факторов
требуется наилучшим образом описать вектором общих факторов 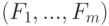 размерности
размерности  . Новые показатели
. Новые показатели 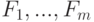 должны удовлетворять следующему условию
должны удовлетворять следующему условию
(Отметьте один правильный вариант ответа.)
Варианты ответа
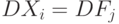 , при
, при 
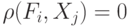 при
при 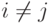
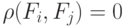 при
при 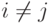 (Верный ответ)
(Верный ответ)

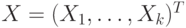 представлен в виде
представлен в виде 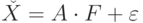 ,где F- вектор общих факторов размерности
,где F- вектор общих факторов размерности 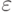 - вектор случайных погрешностей размерности k, А - матрица нагрузок размерности
- вектор случайных погрешностей размерности k, А - матрица нагрузок размерности 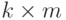 . Элементы
. Элементы 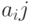 ,
,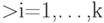
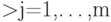 матрицы А - это
матрицы А - это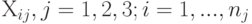 описываются моделью следующего вида
описываются моделью следующего вида  , где
, где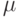 -неизвестное общее среднее,
-неизвестное общее среднее, 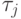 -отклонение от среднего, вызванное изменением уровня факторной переменной,
-отклонение от среднего, вызванное изменением уровня факторной переменной, 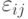 - погрешности с нулевым математическим ожиданием.Контраст
- погрешности с нулевым математическим ожиданием.Контраст 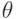 параметров
параметров 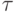 в этой модели задан следующим образом
в этой модели задан следующим образом 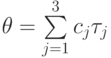 , где
, где  .Определенный таким образом контраст характеризует
.Определенный таким образом контраст характеризует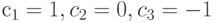 .Определенный таким образом контраст характеризует
.Определенный таким образом контраст характеризует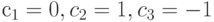 .Определенный таким образом контраст характеризует
.Определенный таким образом контраст характеризует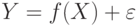 , в которой
, в которой  и
и  – наблюдаемые случайные величины, а
– наблюдаемые случайные величины, а  - ненаблюдаемая случайная помеха с нулевым математическим ожиданием. Предполагается, что случайные величины X и
- ненаблюдаемая случайная помеха с нулевым математическим ожиданием. Предполагается, что случайные величины X и 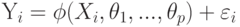 ,
, 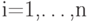 , где
, где 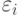 - ненаблюдаемые центрированные погрешности, имеющие плотность распределения
- ненаблюдаемые центрированные погрешности, имеющие плотность распределения 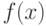 . Для оценивания неизвестных параметров
. Для оценивания неизвестных параметров 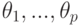 применен ранговый метод. Величины дисперсий
применен ранговый метод. Величины дисперсий 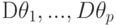 , полученных R-оценок, зависят от
, полученных R-оценок, зависят от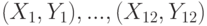 вычислен выборочный коэффициент корреляции
вычислен выборочный коэффициент корреляции 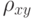 . Какое распределение имеет статистика
. Какое распределение имеет статистика 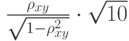 в том случае, когда случайные величины
в том случае, когда случайные величины 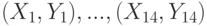 вычислен выборочный коэффициент корреляции
вычислен выборочный коэффициент корреляции 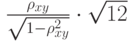 в том случае, когда случайные величины
в том случае, когда случайные величины