Чему равна сумма квадратов и произведение всех комплексных корней многочлена: 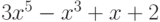 ?
?
(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа



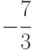

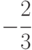 (Верный ответ)
(Верный ответ)


 (Верный ответ)
(Верный ответ)
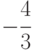

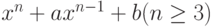 ?
? из единицы?
из единицы?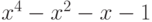 ?
?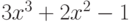 ?
? в правом ортонормированном базисе
в правом ортонормированном базисе  , если
, если 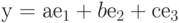 (а, b, с — заданные числа); у — фиксированный вектор линейного пространства
(а, b, с — заданные числа); у — фиксированный вектор линейного пространства 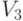 ,
,  из
из ![\widehat А х = [х , у], где [х , у]](https://intuit.ru//sites/default/files/tex_cache/bb53811acdf9d1592baa14383e89273e.png) — векторное произведение вектора
— векторное произведение вектора  ?
?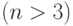 , у которых сумма первых трех элементов равна нулю?
, у которых сумма первых трех элементов равна нулю?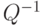 от ортонормированного базиса
от ортонормированного базиса 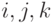 в пространстве
в пространстве 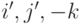 , где векторы
, где векторы  получаются соответственно из векторов
получаются соответственно из векторов  и
и  поворотом их на угол
поворотом их на угол  в плоскости этих векторов?
в плоскости этих векторов?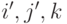 , где векторы
, где векторы 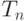 , сумма элементов которых равна нулю, которое изоморфно пространству
, сумма элементов которых равна нулю, которое изоморфно пространству 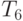 ?
?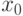 многочлена
многочлена  , где
, где  ,
, 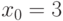 ?
?