Какие условия являются достаточными для того, чтобы предел сложной функции ![y = f[\varphi (x)]](https://intuit.ru//sites/default/files/tex_cache/ead719ea19850ef1759fce07ef02772d.png) существовал:
существовал:
(Отметьте один правильный вариант ответа.)
Варианты ответа
существует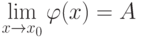 и
и 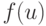 непрерывна в точке
непрерывна в точке 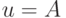 (Верный ответ)
(Верный ответ)
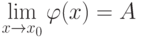 и
и 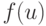 непрерывна в точке
непрерывна в точке 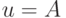 (Верный ответ)
(Верный ответ)
существует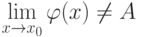 и
и 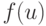 непрерывна в точке
непрерывна в точке 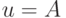
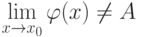 и
и 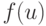 непрерывна в точке
непрерывна в точке 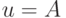
существует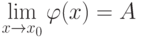 и
и 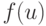 разрывна в точке
разрывна в точке 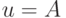
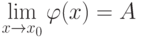 и
и 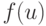 разрывна в точке
разрывна в точке 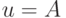

![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) функции
функции  должны выполняться, чтобы
должны выполняться, чтобы 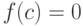 для некоторой точки
для некоторой точки  :
: непрерывна в точке
непрерывна в точке  , а функция
, а функция  непрерывна в точке
непрерывна в точке  , то сложная функция
, то сложная функция 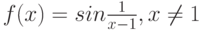 является достаточным для того, чтобы функция
является достаточным для того, чтобы функция 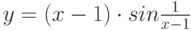 являлась бесконечно малой при
являлась бесконечно малой при 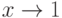 (
(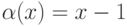 - б.м.ф. при
- б.м.ф. при  является достаточным для того, чтобы функция
является достаточным для того, чтобы функция 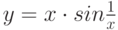 являлась бесконечно малой при
являлась бесконечно малой при  (
( - б.м.ф. при
- б.м.ф. при 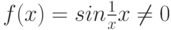 является достаточным для того, чтобы функция
является достаточным для того, чтобы функция  являлась бесконечно малой при
являлась бесконечно малой при 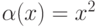 - б.м.ф. при
- б.м.ф. при 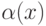 - б.м.ф. при
- б.м.ф. при 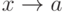 , а функция
, а функция  имеет в точке
имеет в точке  конечный предел, отличный от нуля, то предел частного
конечный предел, отличный от нуля, то предел частного 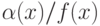
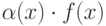
 . Тогда (
. Тогда ( такова, что интервал
такова, что интервал 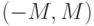 при любом
при любом 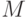 содержит только конечное число членов последовательности, то ее предел
содержит только конечное число членов последовательности, то ее предел  равен
равен 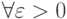 неравенство
неравенство  выполняется лишь для конечного числа членов последовательности, то её предел
выполняется лишь для конечного числа членов последовательности, то её предел