Введение в математический анализ - ответы
Количество вопросов - 258
Если общий член последовательности  определяется формулой
определяется формулой 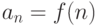 , то
, то  равен
равен
Пусть 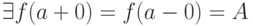 , тогда
, тогда
Пусть  . Тогда
. Тогда
По определению,  , если
, если
Предел функции 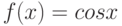 на бесконечности
на бесконечности
Функция 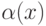 называется бесконечно большой функцией при
называется бесконечно большой функцией при  , стремящемся к
, стремящемся к  , если
, если 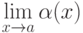 равен
равен
Если 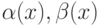 - бесконечно малые функции при
- бесконечно малые функции при 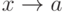 , то
, то 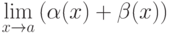
Число  является
является
По определению (Коши),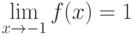 , если
, если 
Пусть  определена в некоторой окрестности точки
определена в некоторой окрестности точки  и
и  . Тогда (
. Тогда (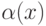 - б.м.ф. при
- б.м.ф. при 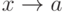 ). Тогда предел функции
). Тогда предел функции 
Пусть функции 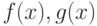 определены в некоторой окрестности точки
определены в некоторой окрестности точки  и
и 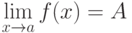 . Тогда
. Тогда
Какие из перечисленных функций непрерывны в точке  :
:
Какие из перечисленных ниже множеств являются ограниченными сверху множествами:
Последовательность  , где
, где 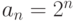 является
является
Для какого множества из непрерывности функции на нём следует её равномерная непрерывность:
Если все частичные пределы последовательности одинаковы и равны  , то
, то
Чему эквивалентна функция 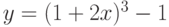 при
при 
Если последовательность  имеет конечный предел, то эта последовательность
имеет конечный предел, то эта последовательность
Последовательность  называется бесконечно малой, если
называется бесконечно малой, если  равен
равен
Последовательность  монотонно возрастает, а
монотонно возрастает, а 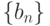 убывает, причем
убывает, причем  и
и 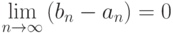 . Тогда по принципу вложенных отрезков
. Тогда по принципу вложенных отрезков
Какая из перечисленных функций является б.м.ф. при 
![\lim\limits_{n \to \infty} {\frac {\sqrt[3]{n^2 - 1}} {\sqrt[3]{n + 1} - \sqrt[3]{n}}}](https://intuit.ru//sites/default/files/tex_cache/fe94e876223ddbf7221862f418c108e3.png) равен
равен
Чему эквивалентна функция 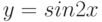 при
при 
Пусть 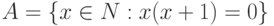 . Какое из перечисленных множеств есть множество
. Какое из перечисленных множеств есть множество  :
:
Указать числовой промежуток, на котором функция 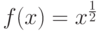 непрерывна:
непрерывна:
Пусть задана функция 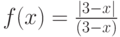 . Тогда
. Тогда
Если функция  непрерывна на отрезке
непрерывна на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) и
и  , то
, то
Какое из перечисленных ниже множеств является окрестностью точки 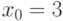
Пусть 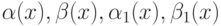 - бесконечно малые при
- бесконечно малые при 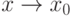 функции, причём
функции, причём 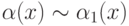 и
и 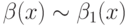 . Если
. Если 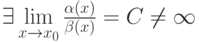 , то
, то
Пусть 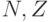 и
и  - множества натуральных, целых и рациональных чисел. Какая из записей верна:
- множества натуральных, целых и рациональных чисел. Какая из записей верна:
Пусть  (числа кратные 8-ми). Какое из перечисленных множеств есть множество
(числа кратные 8-ми). Какое из перечисленных множеств есть множество  :
:
Пусть  и
и 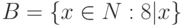 . Какое множество является пересечением
. Какое множество является пересечением 
Какое из предложенных числовых множеств является конечным:
Множество А называется счётным, если оно эквивалентно:
Число 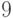 является
является
Выражение 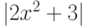 равно
равно
Пусть  . Какие неравенства ему равносильны:
. Какие неравенства ему равносильны:
Для модуля  разности двух чисел выбрать справедливое утверждение:
разности двух чисел выбрать справедливое утверждение:
Какое подмножество числовой прямой равносильно неравенству  :
:
Какое из перечисленных ниже множеств является окрестностью точки 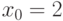
Какое из неравенств задаёт 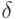 -окрестность точки
-окрестность точки 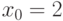
Какое из перечисленных ниже множеств является множеством всех нижних граней для  :
:
Какое условие является достаточным для существования точной нижней грани множества:
Пусть задано множество 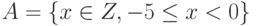 .Отметьте верные утверждения
.Отметьте верные утверждения
Десятый член последовательности 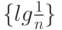 равен
равен
Пусть число  - предел последовательности
- предел последовательности  . Тогда
. Тогда 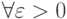 вне окрестности
вне окрестности 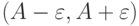 лежит
лежит
Последовательность  является
является
Дана сходящаяся последовательность  . Если
. Если 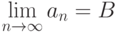 , то
, то
Если 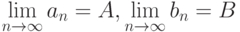 , то предел последовательности
, то предел последовательности 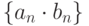
Последовательность  называется ограниченной сверху, если
называется ограниченной сверху, если 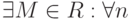
Последовательность  , где
, где  является
является
Если последовательность  является бесконечно большой, причем
является бесконечно большой, причем 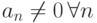 . Тогда
. Тогда 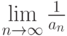 равен
равен
Последовательность  называется неубывающей, если
называется неубывающей, если 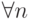
Последовательность  ,
,  является
является
Если последовательность  убывает, то ее неограниченность означает, что
убывает, то ее неограниченность означает, что  равен
равен
Для сходимости монотонной последовательности достаточно (и необходимо), чтобы она была
Вычислить предел данной последовательности: 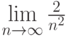
Вычислить предел данной последовательности: 
Вычислить предел данной последовательности: 
Вычислить предел данной последовательности: ![\lim\limits_{n \to \infty} {[\frac {1} {3n} cos \frac {2} {n^2} - \frac {2n} {2-n}]}](https://intuit.ru//sites/default/files/tex_cache/b9273d961683dfcbc17b377191a4fed9.png)
Указать область определения функции 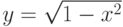
По определению (Коши),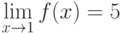 , если
, если 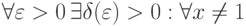
Если  и
и  , то
, то
Какое свойство функции  в некоторой окрестности точки
в некоторой окрестности точки  является необходимым для существования конечного предела
является необходимым для существования конечного предела  в точке
в точке  :
:
По определению, 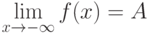 , если
, если
Функция 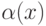 называется бесконечно малой функцией при
называется бесконечно малой функцией при  , стремящемся к
, стремящемся к  , если
, если 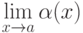 равен
равен
Какая из перечисленных функций является б.б.ф. при 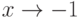
Если 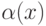 - б.м.ф. при
- б.м.ф. при 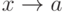 , а функция
, а функция  имеет в точке
имеет в точке  конечный предел, отличный от нуля, то предел частного
конечный предел, отличный от нуля, то предел частного 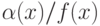
Какое свойство функции 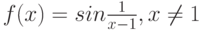 является достаточным для того, чтобы функция
является достаточным для того, чтобы функция 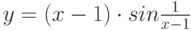 являлась бесконечно малой при
являлась бесконечно малой при 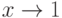 (
(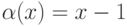 - б.м.ф. при
- б.м.ф. при 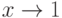 ):
):
Пусть функции 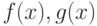 определены в некоторой окрестности точки
определены в некоторой окрестности точки  и
и 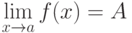 ,. Тогда
,. Тогда
Если функция  - бесконечно большая функция при
- бесконечно большая функция при 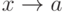 , то предел функции
, то предел функции  равен
равен
Предел слева  , если
, если
Какое условие является критерием существования предела функции в точке  :
:
По определению (Гейне), функция  называется непрерывной в точке
называется непрерывной в точке  , если
, если 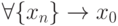 , соответствующая
, соответствующая 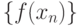
Если функция  непрерывна в точке
непрерывна в точке  и
и 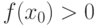 ,то
,то
Указать числовой промежуток, на котором функция  непрерывна:
непрерывна:
Отметьте верные утверждения
Если функция  непрерывна в точке
непрерывна в точке  , а функция
, а функция  непрерывна в точке
непрерывна в точке  , то сложная функция
, то сложная функция ![y = f[\varphi (x)]](https://intuit.ru//sites/default/files/tex_cache/ead719ea19850ef1759fce07ef02772d.png)
Как представить функцию 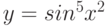 в виде композиции непрерывных функций
в виде композиции непрерывных функций 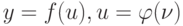 и
и 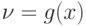
Если функция  непрерывна в точке
непрерывна в точке  , то односторонние пределы в этой точке
, то односторонние пределы в этой точке
Точка  называется точкой разрыва функции
называется точкой разрыва функции  второго рода , если в точке
второго рода , если в точке 
Точка 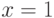 для функции
для функции  является точкой разрыва
является точкой разрыва
Какие условия для непрерывной на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) функции
функции  должны выполняться, чтобы
должны выполняться, чтобы 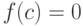 для некоторой точки
для некоторой точки  :
:
Множеством значений функции ![y = cos x, x \in [\frac \pi 2, \pi]](https://intuit.ru//sites/default/files/tex_cache/1395ffae9c03a735464f9cbcc1564482.png) является
является
Если функция  непрерывна на отрезке
непрерывна на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) , то
, то
На каком множестве должна быть непрерывна функция  для того, чтобы она на этом множестве принимала свои наименьшее и наибольшее значения:
для того, чтобы она на этом множестве принимала свои наименьшее и наибольшее значения:
Функция называется равномерно непрерывной на интервале 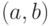 , если
, если
Пусть 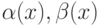 б.м.ф. при
б.м.ф. при  и
и 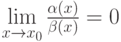 . Тогда
. Тогда
Пусть 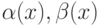 б.м.ф. при
б.м.ф. при  и
и 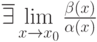 .Тогда
.Тогда
Чему эквивалентна функция 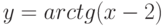 при
при 
Чему эквивалентна функция 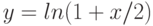 при
при 
Если 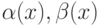 и
и 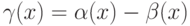 - б.м.ф. при
- б.м.ф. при 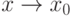 . Какое условие необходимо и достаточно для того, чтобы
. Какое условие необходимо и достаточно для того, чтобы 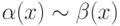
Что является асимптотической формулой для  при
при 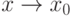
Что является асимптотической формулой для 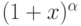 при
при 
Пусть  . Тогда
. Тогда
Какие из множеств являются подмножеством множества  :
:
Функция 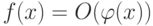 при
при 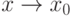 , если
, если
Какое условие является достаточным для существования точной верхней грани множества:
Какое свойство функции 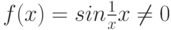 является достаточным для того, чтобы функция
является достаточным для того, чтобы функция  являлась бесконечно малой при
являлась бесконечно малой при  (
(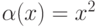 - б.м.ф. при
- б.м.ф. при  ):
):
Пусть задано множество  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Функция 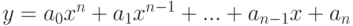 является непрерывной в силу теоремы
является непрерывной в силу теоремы
Какое подмножество числовой прямой равносильно неравенству 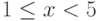 :
:
Пусть функции 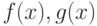 определены в некоторой окрестности точки
определены в некоторой окрестности точки  и
и 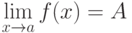 . Тогда
. Тогда
Выражение  равно
равно
Точка 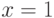 для функции
для функции 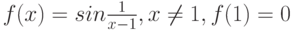 является точкой разрыва
является точкой разрыва
Последовательность  ,
,  является
является
По определению  , функция
, функция  называется непрерывной в точке
называется непрерывной в точке  , если
, если
Если функция 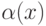 - бесконечно малая функция при
- бесконечно малая функция при 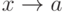 , то функция
, то функция 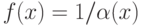
Какие условия должны выполняться, чтобы 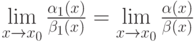
По определению, число  называется пределом последовательности
называется пределом последовательности  , если
, если 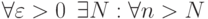 справедливо неравенство
справедливо неравенство
Если функция  непрерывна на отрезке
непрерывна на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) , то она на нём
, то она на нём
Предел функции  на бесконечности
на бесконечности
Если последовательность  бесконечно большая, то она
бесконечно большая, то она
Если последовательность  возрастает, то ее неограниченность означает, что
возрастает, то ее неограниченность означает, что  равен
равен
Если 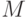 - точная нижняя грань множества
- точная нижняя грань множества 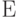 , то эта грань :
, то эта грань :
Какое из перечисленных ниже множеств является множеством всех верхних граней для ![E = [-1,1]:](https://intuit.ru//sites/default/files/tex_cache/58cf9136ba6c11e15833cc6fb69182c6.png)
Какая из функций является ограниченной в некоторой окрестности  , но не имеет конечного предела в этой точке:
, но не имеет конечного предела в этой точке:
Если последовательность  ограниченная, то она
ограниченная, то она
Если  , то последовательность
, то последовательность 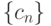
Вычислить предел данной последовательности: 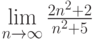
Пусть 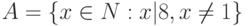 - множество натуральных делителей 8, не равных 1. Какое из перечисленных множеств есть множество
- множество натуральных делителей 8, не равных 1. Какое из перечисленных множеств есть множество  :
:
Какое из предложенных числовых множеств является конечным:
Пусть 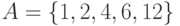 и
и 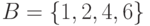 . Какая из записей неверна:
. Какая из записей неверна:
Пусть 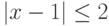 . Какие неравенства ему равносильны:
. Какие неравенства ему равносильны:
Для модуля 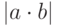 произведения двух чисел выбрать справедливое утверждение:
произведения двух чисел выбрать справедливое утверждение:
Какое подмножество числовой прямой равносильно неравенству 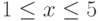 :
:
Какое из неравенств задаёт 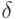 -окрестность точки
-окрестность точки 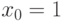
Какие из перечисленных ниже множеств являются ограниченными снизу множествами:
Четвёртый член последовательности 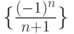 равен
равен
Последовательность называется сходящейся, если её предел
 равен
равен
Последовательность  называется неограниченной, если
называется неограниченной, если 
Последовательность  , где
, где 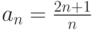 является
является
Запись 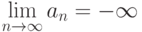 означает, что
означает, что 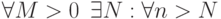
Если последовательность  такова, что
такова, что 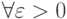 неравенство
неравенство  выполняется лишь для конечного числа членов последовательности, то её предел
выполняется лишь для конечного числа членов последовательности, то её предел  равен
равен
Если последовательность  возрастает и ее точная верхняя грань
возрастает и ее точная верхняя грань 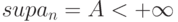 , то предел последовательности
, то предел последовательности  равен
равен
По определению (Коши),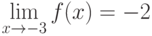 , если
, если 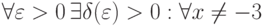
Если 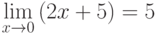 и
и 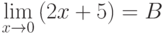 , то
, то
Отметьте верные утверждения:
Какая из функций имеет предел на бесконечности, равный нулю:
Какая из перечисленных функций является б.м.ф. при 
Какое условие является достаточным для того, чтобы сумма двух функций  была бесконечно малой при при
была бесконечно малой при при 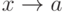 :
:
Если 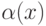 - б.м.ф. при
- б.м.ф. при 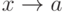 , а функция
, а функция  ограничена в окрестности
ограничена в окрестности  , то предел произведения
, то предел произведения 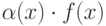
Если функция 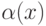 - бесконечно малая функция при
- бесконечно малая функция при 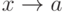 , то предел функции
, то предел функции 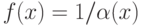 равен
равен
Число А называется пределом функции  слева
слева 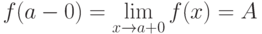 , если
, если
По определению  , функция
, функция  называется непрерывной в точке
называется непрерывной в точке  , если
, если 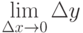
Какие из перечисленных функций непрерывны в точке  :
:
Отметьте верные утверждения
Какие условия являются достаточными для того, чтобы предел сложной функции ![y = f[\varphi (x)]](https://intuit.ru//sites/default/files/tex_cache/ead719ea19850ef1759fce07ef02772d.png) существовал:
существовал:
Точка 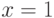 для функции
для функции 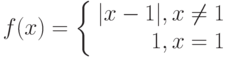 является точкой разрыва
является точкой разрыва
Пусть 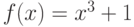 . Сколько корней имеет данный многочлен:
. Сколько корней имеет данный многочлен:
Если функция  непрерывна на отрезке
непрерывна на отрезке ![[a,b], f(a) = A, f(b) = B](https://intuit.ru//sites/default/files/tex_cache/530663b6c2ab1bd03cb2a940588e60b8.png) то
то
Какое условие является достаточным для ограниченности функции  на множестве
на множестве
Если функция  непрерывна на отрезке
непрерывна на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) , то
, то
Чему эквивалентна функция  при
при 
Чему эквивалентна функция 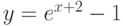 при
при 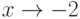
Пусть 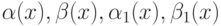 - бесконечно малые при
- бесконечно малые при 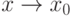 функции, причём
функции, причём 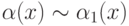 и
и 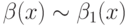 . Если
. Если 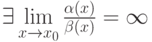 , то
, то
Если 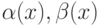 - б.м.ф. при
- б.м.ф. при 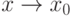 ,
, 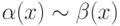 и
и 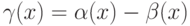 , то
, то
Что является асимптотической формулой для  при
при 
Какое из заданных ниже соответствий является взаимно однозначным:
Последовательность  ,
,  является
является
Пусть 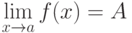 , тогда
, тогда
Какая из указанных функций является равномерно непрерывной на интервале 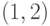 :
:
Пусть 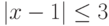 . Какое неравенство ему равносильно?
. Какое неравенство ему равносильно?
Последовательность  , у которой существуют хотя бы два различных частичных предела
, у которой существуют хотя бы два различных частичных предела  и
и  ,
, 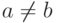
Точка  называется точкой устранимого разрыва функции
называется точкой устранимого разрыва функции  , если в этой точке
, если в этой точке 
Пусть функции 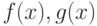 определены в некоторой окрестности точки
определены в некоторой окрестности точки  и
и 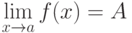 . Тогда
. Тогда
Если 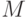 - точная верхняя грань множества
- точная верхняя грань множества 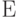 , то эта грань
, то эта грань
Последовательность  , где
, где  является
является
Как представить функцию 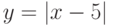 в виде композиции двух непрерывных функций
в виде композиции двух непрерывных функций  и
и 
Какое из неравенств задаёт 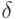 -окрестность точки
-окрестность точки 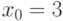
Указать область определения функции 
Отметьте верные утверждения
Вычислить предел данной последовательности: 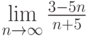
Б.м.ф. 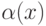 при
при  имеет порядок малости
имеет порядок малости  , если
, если
Пусть  - множество простых чисел и
- множество простых чисел и  - натуральных. Какая из записей верна:
- натуральных. Какая из записей верна:
Пусть  и
и  , где операция
, где операция  - означает, что
- означает, что  является делителем
является делителем  . Какое множество является пересечением
. Какое множество является пересечением  ?
?
Какое из предложенных числовых множеств является бесконечным:
Для модуля 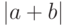 суммы двух чисел выбрать справедливое утверждение:
суммы двух чисел выбрать справедливое утверждение:
Какое из перечисленных ниже множеств является окрестностью точки 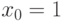
Какое из перечисленных ниже множеств является ограниченным множеством:
Если  , то последовательность
, то последовательность 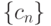
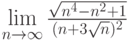 равен
равен
Если последовательность  такова, что интервал
такова, что интервал 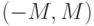 при любом
при любом 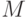 содержит только конечное число членов последовательности, то ее предел
содержит только конечное число членов последовательности, то ее предел  равен
равен
Вычислить предел данной последовательности: 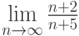
Вычислить предел данной последовательности: 
Вычислить предел данной последовательности: 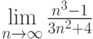
Указать область определения функции 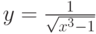
По определению (Коши),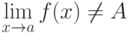 , если
, если
Если 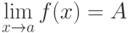 и
и  , то
, то
По определению, 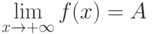 , если
, если
Какая из функций имеет предел на бесконечности, равный нулю:
Какая из перечисленных функций является б.б.ф. при 
Если  , а функция
, а функция  ограничена в окрестности
ограничена в окрестности  , то предел произведения
, то предел произведения 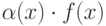
Функция  непрерывна в точке
непрерывна в точке  , если односторонние пределы в этой точке
, если односторонние пределы в этой точке
Точка 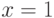 для функции
для функции  является точкой разрыва
является точкой разрыва
Пусть 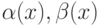 б.м.ф. при
б.м.ф. при  и
и  . Тогда
. Тогда
Пусть 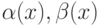 б.м.ф. при
б.м.ф. при  и
и 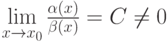 . Тогда
. Тогда
Если 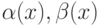 - б.м.ф. при
- б.м.ф. при 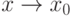 ,
, 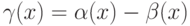 и
и 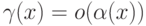 , то
, то
Пусть 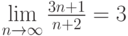 . Тогда, по определению предела,
. Тогда, по определению предела, 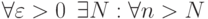
Какие из перечисленных функций непрерывны в точке 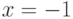 :
:
Какое из перечисленных ниже множеств является множеством всех верхних граней для ![E = (-\infty,1]](https://intuit.ru//sites/default/files/tex_cache/abdb782e35b9eecb1859cc1ce1947adf.png) :
:
Если последовательность  убывает и ее точная нижняя грань
убывает и ее точная нижняя грань  то предел последовательности
то предел последовательности 
Даны две сходящиеся последовательности: 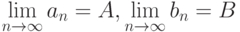 , причем
, причем 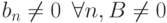 . Тогда предел последовательности
. Тогда предел последовательности 
Пусть функция 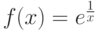 ,
, 
Число  является
является
Число  называется пределом последовательности
называется пределом последовательности  , если
, если
Последовательность  называется ограниченной снизу, если
называется ограниченной снизу, если 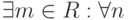
По определению, запись 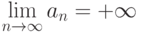 означает, что
означает, что 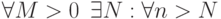
Необходимое и достаточное условие сходимости последовательности  (критерий Коши ) формулируется следующим образом:
(критерий Коши ) формулируется следующим образом: 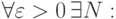
Указать область определения функции 
По определению (Коши), 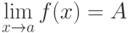 , если
, если
Функция 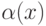 называется бесконечно малой функцией при
называется бесконечно малой функцией при  , стремящемся к
, стремящемся к  , если
, если 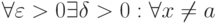
Какое свойство функции  является достаточным для того, чтобы функция
является достаточным для того, чтобы функция 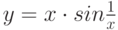 являлась бесконечно малой при
являлась бесконечно малой при  (
( - б.м.ф. при
- б.м.ф. при  ):
):
Пусть  определена в некоторой окрестности точки
определена в некоторой окрестности точки  и
и 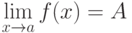 . Тогда (
. Тогда (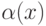 - б.м.ф. при
- б.м.ф. при 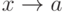 )
)
Если функция  - бесконечно большая функция при
- бесконечно большая функция при 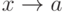 , то функция
, то функция 
Предел справа 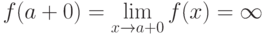 , если
, если
Если функция  непрерывна в точке
непрерывна в точке  и
и 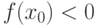 ,то
,то 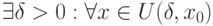
Указать числовой промежуток, на котором функция  непрерывна:
непрерывна:
Точка  называется точкой разрыва функции
называется точкой разрыва функции  с конечным скачком функции, если в точке
с конечным скачком функции, если в точке 
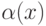 называется б.м. более высокого порядка, чем
называется б.м. более высокого порядка, чем 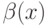 при
при  , если
, если
Число А называется пределом функции  справа
справа 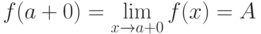 , если
, если
Вычислить предел данной последовательности: 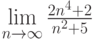
По определению, функция  называется непрерывной в точке
называется непрерывной в точке  , если
, если
Чему эквивалентна функция 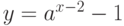 при
при 
Выражение 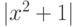 равно
равно
Пусть для функции  выполнено условие
выполнено условие  . Это означает, что функция
. Это означает, что функция 
Если последовательность  является бесконечно малой, а
является бесконечно малой, а 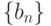 - ограниченной (
- ограниченной (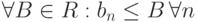 ) , то
) , то  равен
равен
Даны две сходящиеся последовательности: 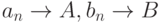 . Предел последовательности
. Предел последовательности 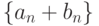 равен
равен
Пусть  и
и  . Какое множество является объединением
. Какое множество является объединением 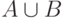
Последовательность  является
является
 равен
равен
Последовательность  называется ограниченной, если
называется ограниченной, если 
Последовательность  называется невозрастающей, если
называется невозрастающей, если 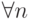
Если функция  определена в
определена в  - окрестности точки
- окрестности точки  и
и  , то в некоторой окрестности точки
, то в некоторой окрестности точки  функция
функция
Какое условие является достаточным для равенства нулю предела суммы двух функций  при
при 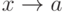 :
:
Как представить функцию 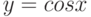 в виде композиции двух непрерывных функций
в виде композиции двух непрерывных функций  и
и 
Пусть 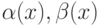 б.м.ф. при
б.м.ф. при  и
и 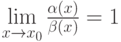 . Тогда
. Тогда
Если функция  непрерывна в точке
непрерывна в точке  и
и 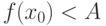 ,то
,то
По определению, последовательность  называется бесконечно большой (
называется бесконечно большой ( ) , если
) , если 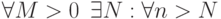
Вычислить предел данной последовательности: ![\lim\limits_{n \to \infty} {[\frac {1} {n^2} sin \frac {1} {n^2} - \frac {6n} {2-3n}]}](https://intuit.ru//sites/default/files/tex_cache/2dee43663186dd0f4a70ffe8af89a361.png)
Если 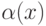 - б.м.ф. при
- б.м.ф. при 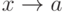 , а функция
, а функция  имеет конечный предел в точке
имеет конечный предел в точке  , то предел произведения
, то предел произведения 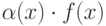
Точка 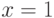 для функции
для функции 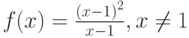 является точкой разрыва
является точкой разрыва
Пусть 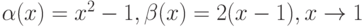 . Тогда
. Тогда
Что является асимптотической формулой для 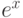 при
при 
Множеством значений функции ![y = sin x, x \in [0, \frac \pi 2]](https://intuit.ru//sites/default/files/tex_cache/c14cc031fbfc7f0f327f1ce191f285b5.png) является
является
Функция 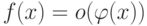 при
при 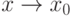 , если
, если
Число  является
является
Если последовательность  является бесконечно малой, причем
является бесконечно малой, причем 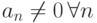 , тогда
, тогда 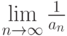 равен
равен
Вычислить предел данной последовательности: 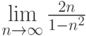
Пусть 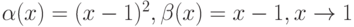 . Тогда
. Тогда
Чему эквивалентна функция 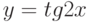 при
при 
Если функция  непрерывна в точке
непрерывна в точке  и
и 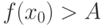 ,то
,то

 в некоторой окрестности точки
в некоторой окрестности точки  является необходимым для существования конечного предела
является необходимым для существования конечного предела  в точке
в точке  :
: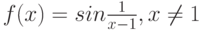 является достаточным для того, чтобы функция
является достаточным для того, чтобы функция 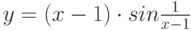 являлась бесконечно малой при
являлась бесконечно малой при 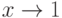 (
(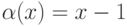 - б.м.ф. при
- б.м.ф. при 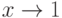 ):
): для того, чтобы она на этом множестве принимала свои наименьшее и наибольшее значения:
для того, чтобы она на этом множестве принимала свои наименьшее и наибольшее значения: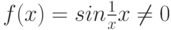 является достаточным для того, чтобы функция
является достаточным для того, чтобы функция  являлась бесконечно малой при
являлась бесконечно малой при  (
(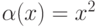 - б.м.ф. при
- б.м.ф. при  ):
): , но не имеет конечного предела в этой точке:
, но не имеет конечного предела в этой точке: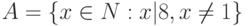 - множество натуральных делителей 8, не равных 1. Какое из перечисленных множеств есть множество
- множество натуральных делителей 8, не равных 1. Какое из перечисленных множеств есть множество  :
: такова, что
такова, что 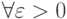 неравенство
неравенство  выполняется лишь для конечного числа членов последовательности, то её предел
выполняется лишь для конечного числа членов последовательности, то её предел  равен
равен была бесконечно малой при при
была бесконечно малой при при 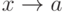 :
: такова, что интервал
такова, что интервал 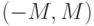 при любом
при любом 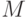 содержит только конечное число членов последовательности, то ее предел
содержит только конечное число членов последовательности, то ее предел  равен
равен  (критерий Коши ) формулируется следующим образом:
(критерий Коши ) формулируется следующим образом: 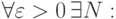
 является достаточным для того, чтобы функция
является достаточным для того, чтобы функция 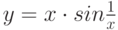 являлась бесконечно малой при
являлась бесконечно малой при  (
( - б.м.ф. при
- б.м.ф. при  ):
):