Указать область определения функции 
(Отметьте один правильный вариант ответа.)
Варианты ответа
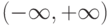
![(-\infty,-1] \cup [1,+\infty)](https://intuit.ru//sites/default/files/tex_cache/b923ba3e3637e90fa78ef500031c53c4.png)
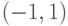 (Верный ответ)
(Верный ответ)
![[-1,1]](https://intuit.ru//sites/default/files/tex_cache/d060b17b29e0dae91a1cac23ea62281a.png)


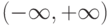
![(-\infty,-1] \cup [1,+\infty)](https://intuit.ru//sites/default/files/tex_cache/b923ba3e3637e90fa78ef500031c53c4.png)
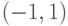 (Верный ответ)
(Верный ответ)
![[-1,1]](https://intuit.ru//sites/default/files/tex_cache/d060b17b29e0dae91a1cac23ea62281a.png)
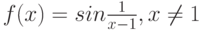 является достаточным для того, чтобы функция
является достаточным для того, чтобы функция 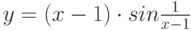 являлась бесконечно малой при
являлась бесконечно малой при 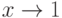 (
(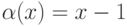 - б.м.ф. при
- б.м.ф. при 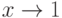 ):
): является достаточным для того, чтобы функция
является достаточным для того, чтобы функция 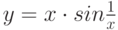 являлась бесконечно малой при
являлась бесконечно малой при  (
( - б.м.ф. при
- б.м.ф. при  ):
):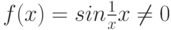 является достаточным для того, чтобы функция
является достаточным для того, чтобы функция  являлась бесконечно малой при
являлась бесконечно малой при  (
(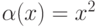 - б.м.ф. при
- б.м.ф. при  ):
):