Присоединенная функция построена в виде так называемого барьера: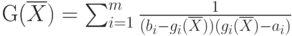 . При этом ограничения в задаче имеют вид:
. При этом ограничения в задаче имеют вид:
(Отметьте один правильный вариант ответа.)
Варианты ответа
 (Верный ответ)
(Верный ответ)



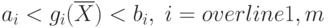 . Тогда присоединенная функция
. Тогда присоединенная функция  . Тогда согласно метода Кэррола присоединенная функция имеет вид:
. Тогда согласно метода Кэррола присоединенная функция имеет вид: . Тогда условия ограничения имеют вид:
. Тогда условия ограничения имеют вид:  определяет базисное решение
определяет базисное решение  согласно симплекс – методу, если ограничения задачи линейного программирования имеют вид:
согласно симплекс – методу, если ограничения задачи линейного программирования имеют вид: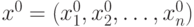 и при этом имеет место равенство
и при этом имеет место равенство  . Это справедливо:
. Это справедливо: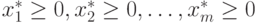 . При этом справедливо равенство:
. При этом справедливо равенство: 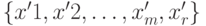 . Связь нового решения
. Связь нового решения 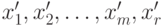 со старым базисным решением
со старым базисным решением  . Тогда уравнение, определяющее старое базисное решение
. Тогда уравнение, определяющее старое базисное решение 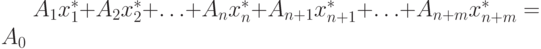 определяет базисное решение
определяет базисное решение