Введение в математическое программирование

Задача линейного программирования сформулирована в каноническом виде:максимизировать $\sum c_i x_i, \; i=1,\ldots,n$ . Тогда условия ограничения имеют вид:

(Отметьте один правильный вариант ответа.)

Варианты ответа

$\begin{aligned}& a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n = b_1 \\& a_{21}x_1 + a_{22}x_2 + \ldots + a_{2n}x_n = b_2 \\& \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\& a_{m1}x_1 + a_{m2}x_2 + \ldots + a_{mn}x_n = b_n, \; x_1 \ge 0, x_2 \ge 0, \ldots, x_n \ge 0 .\end{aligned}$

(Верный ответ)

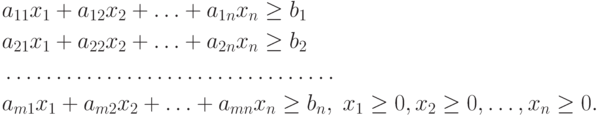
$\begin{aligned}& a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n \ge b_1 \\& a_{21}x_1 + a_{22}x_2 + \ldots + a_{2n}x_n \ge b_2 \\& \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\& a_{m1}x_1 + a_{m2}x_2 + \ldots + a_{mn}x_n \ge b_n, \; x_1 \ge 0, x_2 \ge 0, \ldots, x_n \ge 0 .\end{aligned}$

$\begin{aligned}& a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n \le b_1 \\& a_{21}x_1 + a_{22}x_2 + \ldots + a_{2n}x_n \le b_2 \\& \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\& a_{m1}x_1 + a_{m2}x_2 + \ldots + a_{mn}x_n \le b_n, \; x_1 \ge 0, x_2 \ge 0, \ldots, x_n \ge 0 .\end{aligned}$

Похожие вопросы

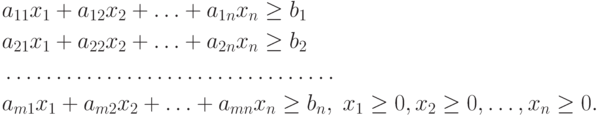
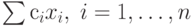Если задача линейного программирования сформулирована следующим образом: максимизировать $\sum с_i x_i, \; i=1,\ldots,n$ , то условия имеют вид:

Пусть задача сформулирована в виде:максимизировать $\sum c_i x_i, \; i=1,\ldots,n$ при условиях

Данная форма записи является:

Если задача сформулирована в виде: максимизировать $\sum с_i x_i, \; i=1,\ldots,n$ при условиях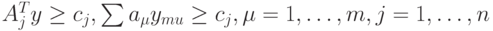

то это задача:

Задача линейного программирования в канонической форме имеет вид: максимизировать L(x) = Σc_jx_j, j=1,...,n при условиях ΣA_jx_j = b, j=1,...,n, x_j ≥ 0. Двойственная задача к ней задача записана так: минимизировать $L'_{\partial e}(y) = \sum b_{\mu} y_{\mu}, \mu = 1,\ldots,m$ при условиях $A^T_j y \ge c_j, \sum a_{\mu} y_{mu} \ge c_j, \mu = 1,\ldots,m, j=1,\ldots,n$ Тогда выполняется условие:

Уравнение $A_1x^*_1 + A_2x^*_2 +\ldots + A_n x^*_n + A_{n+1} x^*_{n+1} +\ldots + A_{n+m}x^*_{n+m} = A_0$ определяет базисное решение $x^*_1, x^*_2, \ldots, x^*_m$ согласно симплекс – методу, если ограничения задачи линейного программирования имеют вид:

Задача линейного программирования сформулирована в матричной форме: максимизировать c^Tx при ограничениях Аx≤b; x≥0;. Тогда ограничения имеют вид:

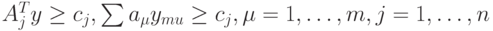Пусть двойственная задача линейного программирования имеет вид: минимизировать $L'_{\partial e}(y) = \sum b_{\mu} y_{\mu}, \mu = 1,\ldots,m$ при условиях $A^T_j y \ge c_j, \sum a_{\mu} y_{mu} \ge c_j, \mu = 1,\ldots,m, j=1,\ldots,n$ и при этом n ≥ m и ранг матрицы A равен m. Тогда задача, записанная в канонической форме, имеет вид:

Если прямая задача линейного программирования имеет вид: максимизировать Σc_jx_j, j=1,...,n при условиях Σa_ijx_j≤b_i, i=1,...,m₁<m; Σa_ijx_j=b_i, i=m₁+1,m₁+2,...,m; x_j≥0; j=1,...,n₁<n. Тогда двойственная ей задача имеет вид: минимизировать Σb_iy_i. Условия ограничения двойственной задачи имеют вид:

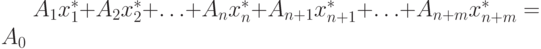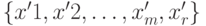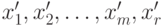Пусть уравнение $A_1 x^*_1 + A_2x^*_2 +\ldots + A_n x^*_n + A_{n+1} x^*_{n+1} +\ldots + A_{n+m}x^*_{n+m} = A_0$ определяет базисное решение $x^*_1, x^*_2, \ldots, x^*_m$ . Обозначим решение уравнения A₁x₁+A₂x₂+...+A_mx_m+A_rx_r = А₀ как $\{ x'1, x'2, \ldots, x'_m, x'_r \}$ . Тогда связь нового решения $x'_1, x'_2, \ldots, x'_m, x'_r$ со старым базисным решением $x^*_1, x^*_2, \ldots, x^*_m$ выражается следующими соотношениями:

Обозначим решение уравнения A₁x₁+A₂x₂+...+A_mx_m+A_rx_r = А₀как $\{ x'1, x'2, \ldots, x'_m, x'_r \}$ . Связь нового решения $x'_1, x'_2, \ldots, x'_m, x'_r$ со старым базисным решением $x^*_1, x^*_2, \ldots, x^*_m$ выражается соотношениями $x'_1 = x^*_1 - x_r x_{1r}; x'_2 = x^*_2 - x_r x_{2r}; \ldots ; x'_m = x^*_m - x_r x_{mr}, x_r$ . Тогда уравнение, определяющее старое базисное решение $x^*_1, x^*_2, \ldots, x^*_m$ , имеет вид:

Введение в математическое программирование

Задача линейного программирования сформулирована в каноническом виде:максимизировать . Тогда условия ограничения имеют вид:

Задача линейного программирования сформулирована в каноническом виде:максимизировать $\sum c_i x_i, \; i=1,\ldots,n$ . Тогда условия ограничения имеют вид: