Введение в математическое программирование

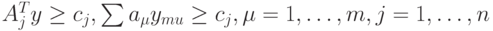Пусть двойственная задача линейного программирования имеет вид: минимизировать $L'_{\partial e}(y) = \sum b_{\mu} y_{\mu}, \mu = 1,\ldots,m$ при условиях $A^T_j y \ge c_j, \sum a_{\mu} y_{mu} \ge c_j, \mu = 1,\ldots,m, j=1,\ldots,n$ и при этом n ≥ m и ранг матрицы A равен m. Тогда задача, записанная в канонической форме, имеет вид:

Варианты ответа

максимизировать L(x) = Σc_jx_j, j=1,...,n при условиях ΣA_jx_j = 0

максимизировать L(x) = Σc_jx_j, j=1,...,n при условиях ΣA_jx_j = b, j=1,...,n, x_j ≥ 0(Верный ответ)

минимизировать L(x) = Σc_jx_j, j=1,...,n при условиях ΣA_jx_j = b, j=1,...,n, x_j ≥ 0

Похожие вопросы

Задача линейного программирования в канонической форме имеет вид: максимизировать L(x) = Σc_jx_j, j=1,...,n при условиях ΣA_jx_j = b, j=1,...,n, x_j ≥ 0. Двойственная задача к ней задача записана так: минимизировать $L'_{\partial e}(y) = \sum b_{\mu} y_{\mu}, \mu = 1,\ldots,m$ при условиях $A^T_j y \ge c_j, \sum a_{\mu} y_{mu} \ge c_j, \mu = 1,\ldots,m, j=1,\ldots,n$ Тогда выполняется условие:

Пусть задача линейного программирования задана в канонической форме: максимизировать L(x) = Σc_jx_j, j=1,...,n при условиях ΣA_jx_j = b, j=1,...,n, x_j ≥ 0. Предположим, что n ≥ m и ранг матрицы A равен m. Тогда двойственная задача имеет вид:

Пусть уравнение $A_1x^*_1 + A_2x^*_2 +\ldots + A_n x^*_n + A_{n+1} x^*_{n+1} +\ldots + A_{n+m}x^*_{n+m} = A_0$ определяет базисное решение $x^*_1, x^*_2, \ldots, x^*_m$ . При этом A_r не входит в базис, т.е. справедливо равенство: A₁x_1r+A₂x_2r+...+A_mx_mr = A_r. Тогда базисное решение имеет вид:

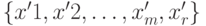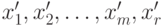Обозначим решение уравнения A₁x₁+A₂x₂+...+A_mx_m+A_rx_r = А₀как $\{ x'1, x'2, \ldots, x'_m, x'_r \}$ . Связь нового решения $x'_1, x'_2, \ldots, x'_m, x'_r$ со старым базисным решением $x^*_1, x^*_2, \ldots, x^*_m$ выражается соотношениями $x'_1 = x^*_1 - x_r x_{1r}; x'_2 = x^*_2 - x_r x_{2r}; \ldots ; x'_m = x^*_m - x_r x_{mr}, x_r$ . Тогда уравнение, определяющее старое базисное решение $x^*_1, x^*_2, \ldots, x^*_m$ , имеет вид:

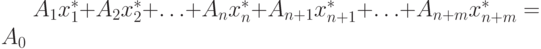Пусть уравнение $A_1 x^*_1 + A_2x^*_2 +\ldots + A_n x^*_n + A_{n+1} x^*_{n+1} +\ldots + A_{n+m}x^*_{n+m} = A_0$ определяет базисное решение $x^*_1, x^*_2, \ldots, x^*_m$ . Обозначим решение уравнения A₁x₁+A₂x₂+...+A_mx_m+A_rx_r = А₀ как $\{ x'1, x'2, \ldots, x'_m, x'_r \}$ . Тогда связь нового решения $x'_1, x'_2, \ldots, x'_m, x'_r$ со старым базисным решением $x^*_1, x^*_2, \ldots, x^*_m$ выражается следующими соотношениями:

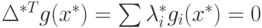Пусть f(x) и все g_i(x) выпуклы и все функции g_i(x) удовлетворяют условию регулярности Слейтера. Задача нелинейного программирования задана следующим образом: минимизировать f(x) при условиях g_i(x) ≤ 0, i = 1,...,m. Пусть существует некоторый вектор Δ^* ≥ 0, такой, что L(x^*,Δ) ≤ L(x^*,Δ^*) ≤ L(x,Δ^*) и $\Delta^{*T}g(x^*) = \sum \lambda^*_i g_i(x^*) = 0$ . Тогда вектор Δ^*:

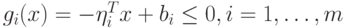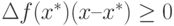Рассмотрим задачу нелинейного программирования: минимизировать f(x) при $g_i(x) = - \eta^T_i x + b_i \le 0, i = 1,\ldots,m$ . Для входящего вектора справедливы следующие условия: $\Delta g^T_i(x – x^*) \le 0$ или $\Delta f(x^*)(x – x^*) \ge 0$ для всех x є S.Тогда скаляры {λ_i}, для которых справедливо соотношение Δf(x^*)=Σλ_iη_i(x) = -Σλ_iΔg_i(x^*), i є I, являются:

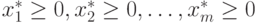Пусть уравнение $A_1x^*_1 + A_2x^*_2 +\ldots + A_n x^*_n + A_{n+1} x^*_{n+1} +\ldots + A_{n+m}x^*_{n+m} = A_0$ определяет базисное решение $x^*_1, x^*_2, \ldots, x^*_m$ , которое является допустимым, т.е. $x^*_1 \ge 0, x^*_2 \ge 0, \ldots, x^*_m \ge 0$ . При этом справедливо равенство: A₁x_1r+A₂x_2r+...+A_mx_mr = A_r. Это значит, что:

Пусть задача сформулирована в виде:максимизировать $\sum c_i x_i, \; i=1,\ldots,n$ при условиях

$\begin{aligned}& a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n = b_1 \\& a_{21}x_1 + a_{22}x_2 + \ldots + a_{2n}x_n = b_2 \\& \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\& a_{m1}x_1 + a_{m2}x_2 + \ldots + a_{mn}x_n = b_n, \; x_1 \ge 0, x_2 \ge 0, \ldots, x_n \ge 0 .\end{aligned}$

Данная форма записи является:

Пусть задача нелинейного программирования задана следующим образом: минимизировать f(x) при условиях g_i(x) ≤ 0, i = 1,...,m. Известно, что существует некоторый вектор Δ^* ≥ 0, такой, что L(x^*,Δ) ≤ L(x^*,Δ^*) ≤ L(x,Δ^*) и $\Delta^{*T}g(x^*) = \sum \lambda^*_i g_i(x^*) = 0$ . Функции g_i(x) удовлетворяют условию регулярности Слейтера. Тогда: