Введение в математическое программирование

Пусть некоторое базисное решение y системы линейных уравнений вида 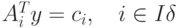$A^T_i y = c_i, \quad i \in I \delta$ , удовлетворяет ограничениям 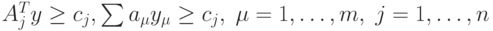$A^T_j y \ge c_j, \sum a_{\mu}y_{\mu} \ge c_j, \; \mu = 1,\ldots,m, \; j = 1,\ldots,n$ Тогда вектора матрицы ограничений прямой задачи 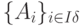$\{ A_i \}_{i \in I \delta}$ , составляющие сопряженный базис, являются:

Варианты ответа

ортонормированными

линейно – независимыми(Верный ответ)

линейно – зависимыми

Похожие вопросы

Пусть для некоторой системы, состоящей из m линейно - независимых векторов матрицы ограничений прямой задачи $\{ A_i \}_{i \in I \delta}$ , базисное решение y соответствующей системы линейных уравнений вида $A^T_i y = c_i, \quad i \in I \delta$ , удовлетворяет ограничениям $A^T_j y \ge c_j, \sum a_{\mu}y_{\mu} \ge c_j, \; \mu = 1,\ldots,m, \; j = 1,\ldots,n$ Тогда данная система носит название:

Сопряженным базисом называется такая система из m линейно - независимых векторов матрицы ограничений прямой задачи $\{ A_i \}_{i \in I \delta}$ , для которой базисное решение y соответствующей системы линейных уравнений вида $A^T_i y = c_i, \quad i \in I \delta$ , удовлетворяет ограничениям:

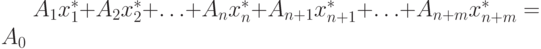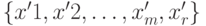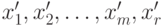Пусть уравнение $A_1 x^*_1 + A_2x^*_2 +\ldots + A_n x^*_n + A_{n+1} x^*_{n+1} +\ldots + A_{n+m}x^*_{n+m} = A_0$ определяет базисное решение $x^*_1, x^*_2, \ldots, x^*_m$ . Обозначим решение уравнения A₁x₁+A₂x₂+...+A_mx_m+A_rx_r = А₀ как $\{ x'1, x'2, \ldots, x'_m, x'_r \}$ . Тогда связь нового решения $x'_1, x'_2, \ldots, x'_m, x'_r$ со старым базисным решением $x^*_1, x^*_2, \ldots, x^*_m$ выражается следующими соотношениями:

Пусть уравнение $A_1 x^*_1 + A_2x^*_2 +\ldots + A_n x^*_n + A_{n+1} x^*_{n+1} +\ldots + A_{n+m}x^*_{n+m} = A_0$ определяет базисное решение $x^*_1, x^*_2, \ldots, x^*_m$ .Новое решение $x'_1, x'_2, \ldots, x'_m, x'_r$ базисное решение связано со старым базисным решением $x^*_1, x^*_2, \ldots, x^*_m$ соотношениями: $x'_1 = x^*_1 - x_r x_{1r}; x'_2 = x^*_2 - x_r x_{2r}; \ldots ; x'_m = x^*_m - x_r x_{mr}, x_r$ . Данное решение будет допустимым, если:

Обозначим решение уравнения A₁x₁+A₂x₂+...+A_mx_m+A_rx_r = А₀как $\{ x'1, x'2, \ldots, x'_m, x'_r \}$ . Связь нового решения $x'_1, x'_2, \ldots, x'_m, x'_r$ со старым базисным решением $x^*_1, x^*_2, \ldots, x^*_m$ выражается соотношениями $x'_1 = x^*_1 - x_r x_{1r}; x'_2 = x^*_2 - x_r x_{2r}; \ldots ; x'_m = x^*_m - x_r x_{mr}, x_r$ . Тогда уравнение, определяющее старое базисное решение $x^*_1, x^*_2, \ldots, x^*_m$ , имеет вид:

Уравнение $A_1x^*_1 + A_2x^*_2 +\ldots + A_n x^*_n + A_{n+1} x^*_{n+1} +\ldots + A_{n+m}x^*_{n+m} = A_0$ определяет базисное решение $x^*_1, x^*_2, \ldots, x^*_m$ . Новое решение $x'_1, x'_2, \ldots, x'_m, x'_r$ связано со старым базисным решением $x^*_1, x^*_2, \ldots, x^*_m$ соотношениями: $x'_1 = x^*_1 - x_r x_{1r}; x'_2 = x^*_2 - x_r x_{2r}; \ldots ; x'_m = x^*_m - x_r x_{mr}, x_r$ Тогда уравнение имеет вид:

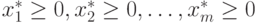Пусть уравнение $A_1x^*_1 + A_2x^*_2 +\ldots + A_n x^*_n + A_{n+1} x^*_{n+1} +\ldots + A_{n+m}x^*_{n+m} = A_0$ определяет базисное решение $x^*_1, x^*_2, \ldots, x^*_m$ . Предположим, что это решение допустимо, т.е. $x^*_1 \ge 0, x^*_2 \ge 0, \ldots, x^*_m \ge 0$ . Если А_r не входит в базис, то:

Пусть уравнение $A_1x^*_1 + A_2x^*_2 +\ldots + A_n x^*_n + A_{n+1} x^*_{n+1} +\ldots + A_{n+m}x^*_{n+m} = A_0$ определяет базисное решение $x^*_1, x^*_2, \ldots, x^*_m$ , которое является допустимым, т.е. $x^*_1 \ge 0, x^*_2 \ge 0, \ldots, x^*_m \ge 0$ . При этом справедливо равенство: A₁x_1r+A₂x_2r+...+A_mx_mr = A_r. Это значит, что:

Пусть уравнение $A_1x^*_1 + A_2x^*_2 +\ldots + A_n x^*_n + A_{n+1} x^*_{n+1} +\ldots + A_{n+m}x^*_{n+m} = A_0$ определяет базисное решение $x^*_1, x^*_2, \ldots, x^*_m$ . При этом A_r не входит в базис, т.е. справедливо равенство: A₁x_1r+A₂x_2r+...+A_mx_mr = A_r. Тогда базисное решение имеет вид:

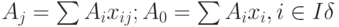Пусть известен некоторый сопряженный базис $\{ A_i \}_{i \in I \delta}$ , которому соответствует псевдоплан x. При этом псевдоплан x является оптимальным решением и $A_j = \sum A_i x_{ij}; A_0 = \sum A_i x_i, i \in I \delta$ Тогда для базисных компонентов справедливо условие: