Сопряженным базисом называется такая система из m линейно - независимых векторов матрицы ограничений прямой задачи 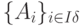 , для которой базисное решение y соответствующей системы линейных уравнений вида
, для которой базисное решение y соответствующей системы линейных уравнений вида 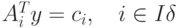 , удовлетворяет ограничениям:
, удовлетворяет ограничениям:
(Отметьте один правильный вариант ответа.)
Варианты ответа


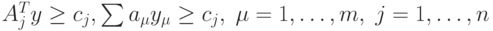 (Верный ответ)
(Верный ответ)

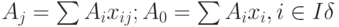 Тогда:
Тогда: определяется уравнением:
определяется уравнением: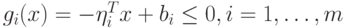 . Для входящего вектора справедливы следующие условия:
. Для входящего вектора справедливы следующие условия:  или
или 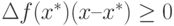 для всех
для всех 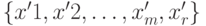 . Связь нового решения
. Связь нового решения 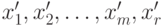 со старым базисным решением
со старым базисным решением  . Тогда уравнение, определяющее старое базисное решение
. Тогда уравнение, определяющее старое базисное решение 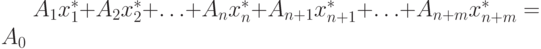 определяет базисное решение
определяет базисное решение