Пусть функции gi(x), i=1,...,m имеют непрерывные частные производные на некотором открытом множестве Rn, содержащем точку x*. Если для функции f(x) ограничения gi(x) ≤ 0, i=1,...,m удовлетворяют условию регулярности в виде линейной независимости векторов Δgi(x*), и существуют такие неотрицательные множители Лагранжа λ1,...,λm, что Δf(x*) + ΣλiΔgi(x*) = 0;Σλigi(x*) = 0, λi ≥ 0, i = 1,...,m является:
Пусть некоторое открытое множество Rn содержит точку x*. Известно, что x* является точкой минимума функции f(x) при ограничениях gi(x) ≤ 0, i=1,...,m, удовлетворяющих условию регулярности в виде линейной независимости векторов Δgi(x*), и существуют такие неотрицательные множители Лагранжа λ1,...,λm, что Δf(x*) + ΣλiΔgi(x*) = 0;Σλigi(x*) = 0, λi ≥ 0, i = 1,...,m. Тогда функции gi(x), i = 1,...,m:
Пусть известен некоторый сопряженный базис
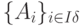
, которому соответствует псевдоплан
x. Базисные компоненты псевдоплана удовлетворяют условиям
xi = xi0≥0 для всех
i є Iδ. При этом псевдоплан
x является оптимальным решением. Тогда справедливы соотношения:
Пусть R – выпуклое множество точек n – мерного пространства. Функция f, определенная на R, удовлетворяет условиям: для любых x1, x2 є R и 0 ≤ k ≤ 1 f[kx1+(1–k)x2] ≤ kf(x1)+(1–k)f(x2). Тогда функция f называется:
Пусть f(x) – строго квазивыпуклая функция. Рассмотрим задачу минимизации f(x) при условии, что x є R, где R – непустое выпуклое множество в Е(n). Если некоторая точка x' является точкой глобального минимума рассматриваемой задачи, то x' одновременно является:
Пусть функции gi(x), i=1,...,m имеют непрерывные частные производные на некотором открытом множестве Rn, содержащем точку x*. Если x* является точкой минимума функции f(x) при ограничениях gi(x) ≤ 0, i=1,...,m, удовлетворяющих условию регулярности в виде линейной независимости векторов Δgi(x*), то существуют такие неотрицательные множители Лагранжа λ1,...,λm, что справедливы соотношения:
Пусть f(x) – строго квазивыпуклая функция. Рассмотрим задачу минимизации f(x) при условии, что x є R, где R – непустое выпуклое множество в Е(n). Пусть x' – точка локального минимума рассматриваемой задачи. Тогда x' является:
Пусть в некоторой задаче минимизации функции f(x), где x є R и R – непустое выпуклое множество в Е(n), точка x' является одновременно точкой и локального, и глобального минимумов. Тогда функция f(x):
Пусть
f(x) и все
gi(x) выпуклы и все функции
gi(x) удовлетворяют условию регулярности Слейтера. Задача нелинейного программирования задана следующим образом: минимизировать
f(x) при условиях
gi(x) ≤ 0, i = 1,...,m. Пусть существует некоторый вектор
Δ* ≥ 0, такой, что
L(x*,Δ) ≤ L(x*,Δ*) ≤ L(x,Δ*) и
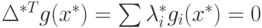
. Тогда вектор
Δ*:
Пусть для некоторой выпуклой вверх(вогнутой) функции f, определенной на множестве R справедливо условие: для любых x1, x2 є R и 0 ≤ k ≤ 1 f[kx1+(1–k)x2] ≤ kf(x1)+(1–k)f(x2). Тогда множество R является:

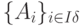 , которому соответствует псевдоплан
, которому соответствует псевдоплан 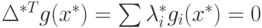 . Тогда вектор
. Тогда вектор