Введение в математическое программирование

Пусть известен некоторый сопряженный базис 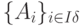$\{ A_i \}_{i \in I \delta}$ , которому соответствует псевдоплан x. Базисные компоненты псевдоплана удовлетворяют условиям x_i = x_i0≥0 для всех i є Iδ. При этом псевдоплан x является оптимальным решением. Тогда справедливы соотношения:

(Отметьте один правильный вариант ответа.)

Варианты ответа

A_j≥ΣA_ix_ij; A₀≥ΣA_ix_i, i є Iδ;

A_j≤ΣA_ix_ij; A₀≤ΣA_ix_i, i є Iδ;

A_j=ΣA_ix_ij; A₀=ΣA_ix_i, i є Iδ. (Верный ответ)

Похожие вопросы

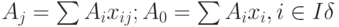Пусть известен некоторый сопряженный базис $\{ A_i \}_{i \in I \delta}$ , которому соответствует псевдоплан x. При этом псевдоплан x является оптимальным решением и $A_j = \sum A_i x_{ij}; A_0 = \sum A_i x_i, i \in I \delta$ Тогда для базисных компонентов справедливо условие:

Пусть задан некоторый сопряженный базис $\{ A_i \}_{i \in I \delta}$ Ему соответствует псевдоплан x. При этом A_j=ΣA_ix_ij; A₀=ΣA_ix_i, i є Iδ. Известно, что задача неразрешима. Это значит, что базисные компоненты удовлетворяют условиям:

Пусть известен некоторый сопряженный базис $\{ A_i \}_{i \in I \delta}$ , которому соответствует псевдоплан x, базисные компоненты которого x_i = x_i0≥0 для всех i є Iδ. При этом $A_j = \sum A_i x_{ij}; A_0 = \sum A_i x_i, i \in I \delta$ Тогда:

Пусть некоторому сопряженному базису $\{ A_i \}_{i \in I \delta}$ соответствует псевдоплан x. Среди базисных компонентов x_i имеются отрицательные, причем для некоторого i: x_i < 0, а все x_ij ≥ 0, j=1,...,n. Это значит, что задача неразрешима. Следовательно, справедливы соотношения:

Пусть некоторому сопряженному базису $\{ A_i \}_{i \in I \delta}$ соответствует псевдоплан x. Очевидно, A_j=ΣA_ix_ij; A₀=ΣA_ix_i, i є Iδ. Известно, что среди базисных компонентов x_i имеются отрицательные, причем для некоторого i: x_i < 0, а все x_ij ≥ 0, j=1,...,n. Это значит, что:

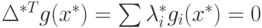Пусть f(x) и все g_i(x) выпуклы и все функции g_i(x) удовлетворяют условию регулярности Слейтера. Задача нелинейного программирования задана следующим образом: минимизировать f(x) при условиях g_i(x) ≤ 0, i = 1,...,m. Пусть существует некоторый вектор Δ^* ≥ 0, такой, что L(x^*,Δ) ≤ L(x^*,Δ^*) ≤ L(x,Δ^*) и $\Delta^{*T}g(x^*) = \sum \lambda^*_i g_i(x^*) = 0$ . Тогда вектор Δ^*:

Пусть задача нелинейного программирования задана следующим образом: минимизировать f(x) при условиях g_i(x) ≤ 0, i = 1,...,m. Известно, что существует некоторый вектор Δ^* ≥ 0, такой, что L(x^*,Δ) ≤ L(x^*,Δ^*) ≤ L(x,Δ^*) и $\Delta^{*T}g(x^*) = \sum \lambda^*_i g_i(x^*) = 0$ . Функции g_i(x) удовлетворяют условию регулярности Слейтера. Тогда:

Пусть f(x) и все g_i(x) выпуклы и все функции g_i(x) удовлетворяют условию регулярности Слейтера. Вектор x^* решением задачи нелинейного программирования: минимизировать f(x) при условиях g_i(x) ≤ 0, i = 1,...,m тогда и только тогда, когда существует такой вектор Δ^* ≥ 0, для которого выполняются условия:

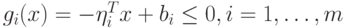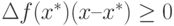Рассмотрим задачу нелинейного программирования: минимизировать f(x) при $g_i(x) = - \eta^T_i x + b_i \le 0, i = 1,\ldots,m$ . Для входящего вектора справедливы следующие условия: $\Delta g^T_i(x – x^*) \le 0$ или $\Delta f(x^*)(x – x^*) \ge 0$ для всех x є S.Тогда скаляры {λ_i}, для которых справедливо соотношение Δf(x^*)=Σλ_iη_i(x) = -Σλ_iΔg_i(x^*), i є I, являются:

Пусть функции g_i(x), i=1,...,m имеют непрерывные частные производные на некотором открытом множестве Rⁿ, содержащем точку x^*. Если x^* является точкой минимума функции f(x) при ограничениях g_i(x) ≤ 0, i=1,...,m, удовлетворяющих условию регулярности в виде линейной независимости векторов Δg_i(x^*), то существуют такие неотрицательные множители Лагранжа λ₁,...,λ_m, что справедливы соотношения: