Пусть требуется изготовить 120 деталей. Их можно изготовить двумя технологическими способами: 1 способ: х1+х12, 2 способ: 2х2+2х22. Затраты связаны функциональной зависимостью. Сколько изделий может быть изготовлено каждым способом?
Пусть требуется изготовить 180 деталей. Их можно изготовить двумя технологическими способами: 1 способ: 4х1+х12, 2 способ: 8х2+х22. Затраты связаны функциональной зависимостью. Сколько изделий может быть изготовлено каждым способом?
Дана функция F(x). Пусть x' доставляет минимум функции F(x) на интервале [a; b] с заданной точностью ξ. Известно, что F1 и F2 – значения функции F(x) в окрестности ±ξ вычисленной точки x=(a+b)/2. При поиске минимума был отброшен отрезок [x; b], т.е. b = x. Это значит, что:
Пусть
f(x) и все
gi(x) выпуклы и все функции
gi(x) удовлетворяют условию регулярности Слейтера. Задача нелинейного программирования задана следующим образом: минимизировать
f(x) при условиях
gi(x) ≤ 0, i = 1,...,m. Пусть существует некоторый вектор
Δ* ≥ 0, такой, что
L(x*,Δ) ≤ L(x*,Δ*) ≤ L(x,Δ*) и
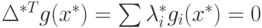
. Тогда вектор
Δ*:
Пусть f(x) – строго квазивыпуклая функция. Рассмотрим задачу минимизации f(x) при условии, что x є R, где R – непустое выпуклое множество в Е(n). Пусть x' – точка локального минимума рассматриваемой задачи. Тогда x' является:
Дана функция F(x). Пусть x' доставляет минимум функции F(x) на интервале [a; b] с заданной точностью ξ. Известно, что F1 и F2 - значения функции F(x) в окрестности ±ξ вычисленной точки x=(a+b)/2. Если F1 < F2, то:
Пусть некоторое открытое множество Rn содержит точку x*. Известно, что x* является точкой минимума функции f(x) при ограничениях gi(x) ≤ 0, i=1,...,m, удовлетворяющих условию регулярности в виде линейной независимости векторов Δgi(x*), и существуют такие неотрицательные множители Лагранжа λ1,...,λm, что Δf(x*) + ΣλiΔgi(x*) = 0;Σλigi(x*) = 0, λi ≥ 0, i = 1,...,m. Тогда функции gi(x), i = 1,...,m:
Пусть задана задача нелинейного программирования: минимизировать
f(x1,...,xn) при условиях
h1(x1,...,xn) = 0;h2(x1,...,xn) = 0;...............hm(x1,...,xn) = 0.
Пусть в некоторой точке
x* ранг матрицы
I = [δhj(x)/δxj], i = 1,...,m; j = 1,...,nравен
m, и существуют
m чисел
λ1,...,λn, не все из которых равны нулю одновременно, и при которых
Δf(x*) + ΣλiΔhi(x) = 0, i = 1,...,m. Тогда в точке
x*:
Пусть функции gi(x), i=1,...,m имеют непрерывные частные производные на некотором открытом множестве Rn, содержащем точку x*. Если для функции f(x) ограничения gi(x) ≤ 0, i=1,...,m удовлетворяют условию регулярности в виде линейной независимости векторов Δgi(x*), и существуют такие неотрицательные множители Лагранжа λ1,...,λm, что Δf(x*) + ΣλiΔgi(x*) = 0;Σλigi(x*) = 0, λi ≥ 0, i = 1,...,m является:
Пусть функции gi(x), i=1,...,m имеют непрерывные частные производные на некотором открытом множестве Rn, содержащем точку x*. Если x* является точкой минимума функции f(x) при ограничениях gi(x) ≤ 0, i=1,...,m, удовлетворяющих условию регулярности в виде линейной независимости векторов Δgi(x*), то существуют такие неотрицательные множители Лагранжа λ1,...,λm, что справедливы соотношения:

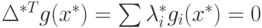 . Тогда вектор
. Тогда вектор