Для некоторого графа построено BFS-дерево с корнем  . Ребро графа
. Ребро графа 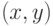 дереву не принадлежит. Какие из следующих соотношений могут выполняться (
дереву не принадлежит. Какие из следующих соотношений могут выполняться ( обозначает расстояние между вершинами в графе)?
обозначает расстояние между вершинами в графе)?
(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
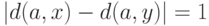 (Верный ответ)
(Верный ответ)
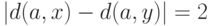
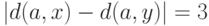
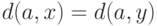 (Верный ответ)
(Верный ответ)

 и
и  - ребра с наименьшими весами в некотором взвешенном графе, причем
- ребра с наименьшими весами в некотором взвешенном графе, причем  . Какие из следующих утверждений верны для любого графа и любой весовой функции?
. Какие из следующих утверждений верны для любого графа и любой весовой функции? с множеством ребер
с множеством ребер  . Для каких из перечисленных ниже семейств
. Для каких из перечисленных ниже семейств  подмножеств множества
подмножеств множества 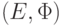 является матроидом для любого графа
является матроидом для любого графа  строится каркас с помощью алгоритма Крускала. Пусть
строится каркас с помощью алгоритма Крускала. Пусть 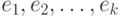 - список всех ребер каркаса в том порядке, в каком они добавлялись при построении. Какие из следующих утверждений верны для любого графа, любой весовой функции и любого
- список всех ребер каркаса в том порядке, в каком они добавлялись при построении. Какие из следующих утверждений верны для любого графа, любой весовой функции и любого 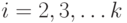 ?
?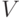 ,
, 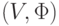 является матроидом,?
является матроидом,? ?
?