Графы и алгоритмы - ответы
Количество вопросов - 122
В графе с весовой функцией  строится каркас с помощью алгоритма Крускала. Пусть
строится каркас с помощью алгоритма Крускала. Пусть 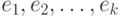 - список всех ребер каркаса в том порядке, в каком они добавлялись при построении. Какие из следующих утверждений верны для любого графа, любой весовой функции и любого
- список всех ребер каркаса в том порядке, в каком они добавлялись при построении. Какие из следующих утверждений верны для любого графа, любой весовой функции и любого 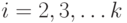 ?
?
В процессе выполнения процедуры поиска в ширину вершины графа делятся на новые, открытые и закрытые. Может ли в графе существовать ребро, соединяющее
В графе K5 все ребра некоторого гамильтонова цикла имеют вес 2, а все остальные ребра - вес 3. Каков будет радиус дерева, построенного для этого графа с помощью алгоритма Дейкстры?
Для некоторого графа построено DFS-дерево и вычислены глубинные номера вершин. Какие из следующих утверждений верны?
Какие из следующих утверждений верны?
Пусть каждая из функций 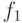 и
и 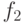 является потоком в некоторой сети. Какие из следующих функций обязательно будут потоками в той же сети?
является потоком в некоторой сети. Какие из следующих функций обязательно будут потоками в той же сети?
Сколько имеется связных абстрактных графов с 4 вершинами?
В дереве имеется ровно три листа 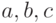 , причем
, причем 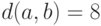 ,
,  ,
, 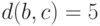 . Сколько всего вершин в этом дереве?
. Сколько всего вершин в этом дереве?
В полном графе с множеством вершин {1, 2, 3, 4, 5, 6} каждое ребро ориентировано от вершины с меньшим номером к вершине с большим. Ребро 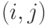 ,
, 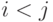 , имеет пропускную способность i . Какова наибольшая величина потока от вершины 1 к вершине 6?
, имеет пропускную способность i . Какова наибольшая величина потока от вершины 1 к вершине 6?
Сколько имеется абстрактных обыкновенных графов с набором степеней (3, 3, 4, 4, 5, 5)?
В связном взвешенном графе для каждой вершины выбрано одно инцидентное ей ребро наибольшего веса. Какие из следующих утверждений верны?
Алгоритм поиска в ширину применяется к планарному графу, заданному матрицей смежности. Какие оценки трудоемкости справедливы в этом случае?
Для каких из перечисленных графов задача о раскраске может быть решена с помощью одних сжатий по включению?
Для двудольного графа построено BFS-дерево с корнем  . Ребро графа
. Ребро графа 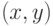 дереву не принадлежит. Какие из следующих соотношений могут выполняться (
дереву не принадлежит. Какие из следующих соотношений могут выполняться ( обозначает расстояние между вершинами в графе)?
обозначает расстояние между вершинами в графе)?
Какие из следующих равенств выполняются для любых графов G1 и G2?
Какое наименьшее число ребер нужно удалить из графа K6, чтобы получился планарный граф?
Какие из следующих графов являются двудольными?
Какие из следующих утверждений верны?
Сколько ребер нужно добавить к наибольшему паросочетанию графа 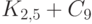 , чтобы получить наименьшее реберное покрытие этого графа?
, чтобы получить наименьшее реберное покрытие этого графа?
Какое из следующих утверждений верно?
BC-дерево некоторого графа имеет радиус 2 и содержит 8 вершин, 4 из которых являются листьями. Сколько шарниров у этого графа?
Дан граф  с множеством вершин
с множеством вершин 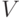 ,
,  - семейство всех независимых множеств вершин этого графа (пустое множество тоже считается независимым). В каких из перечисленных ниже случаев пара
- семейство всех независимых множеств вершин этого графа (пустое множество тоже считается независимым). В каких из перечисленных ниже случаев пара 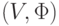 является матроидом,?
является матроидом,?
Что произойдет, если алгоритм СПО применить к матроиду, на множестве элементов которого задана весовая функция с произвольными вещественными значениями (могут быть и отрицательные веса).
Какое наименьшее число ребер нужно удалить из графа K8 , чтобы получился граф, в котором есть эйлеров цикл?
Чему равно число вершинного покрытия графа  ?
?
Какое наименьшее число ребер нужно добавить к графу K3,3, чтобы превратить его в хордальный?
Алгоритм поиска в глубину применяется к планарному графу, заданному списками смежности. Какие оценки трудоемкости справедливы в этом случае?
Какие из следующих утверждений верны для любого взвешенного графа?
Какие из следующих графов изоморфны графу ?
?
Какое наименьшее количество новых ребер нужно добавить к графу C6, чтобы получился непланарный граф?
Сколько имеется ориентированных графов без петель и кратных ребер с множеством вершин {1, 2, 3}?
Сколько имеется абстрактных обыкновенных графов с 5 вершинами и 3 ребрами?
Граф  имеет 4 вершины, а в его матрице смежности 8 единиц. Граф
имеет 4 вершины, а в его матрице смежности 8 единиц. Граф  имеет 5 вершин, а в его матрице смежности 12 единиц. Сколько единиц будет в матрице смежности графа
имеет 5 вершин, а в его матрице смежности 12 единиц. Сколько единиц будет в матрице смежности графа  ?
?
Сколько имеется абстрактных графов с 4 вершинами радиуса 1?
Что происходит с радиусом графа при добавлении нового ребра?
Какие из следующих утверждений верны?
Дерево имеет две центральные вершины, а его радиус равен 6. Чему равен диаметр этого дерева?
Сколько имеется абстрактных двудольных графов с 4 вершинами?
Какое наименьшее число ребер нужно удалить из графа K6, чтобы получился двудольный граф?
В двудольном графе одна доля состоит из пяти вершин степени 2, а другая из трех вершин, две из которых имеют степень 3. Какова степень третьей вершины?
В планарном графе семь вершин, из которых три имеют степень 4, остальные степень 5. Сколько граней будет в плоском изображении этого графа?
Алгоритм поиска в ширину применяется к дереву, заданному списками смежности. Какие оценки трудоемкости справедливы в этом случае?
Пусть h - высота DFS-дерева, построенного для графа G. Какие из следующих утверждений верны?
Для двудольного графа построено DFS-дерево T с корнем a. Ребро графа (x,y) дереву не принадлежит. Какие из следующих соотношений могут выполняться (d обозначает расстояние между вершинами в дереве T)?
G и H - графы с одним и тем же множеством вершин. В графе G 8 ребер, в графе H 9 ребер, а в графе  12 ребер. Сколько ребер в графе
12 ребер. Сколько ребер в графе  ?
?
Какие из следующих утверждений верны для системы фундаментальных циклов, построенной относительно некоторого каркаса?
Какова будет суммарная длина фундаментальных циклов относительно каркаса, построенного с помощью поиска в ширину для графа K7 ?
Какие из следующих утверждений справедливы для любого двусвязного графа?
Какие из следующих утверждений верны?
Чему равно кликовое число графа C9?
Сколько листьев будет в дереве подзадач для задачи о независимом множестве, построенном для графа 3K3?
Какое наименьшее число ребер нужно добавить к графу K3,5, чтобы получился граф, в котором есть эйлеров цикл?
Сколько листьев будет в дереве путей, построенном для графа K4,4?
К графу 2C5 применяется описанный в лекции 11 алгоритм решения задачи о независимом множестве со сжатием по включению. Сколько листьев будет в возникающем при этом дереве подзадач?
Какое наименьшее число ребер нужно удалить из графа  , чтобы превратить его в хордальный?
, чтобы превратить его в хордальный?
Чему равно хроматическое число графа  ?
?
Чему равны хроматические индексы графов K3,3 и C7 ?
В графе с 10 вершинами существует гамильтонов цикл, все ребра которого имеют вес 1. Имеются еще два ребра веса 2, не принадлежащие циклу. Других ребер в графе нет. Каков будет вес оптимального каркаса для этого графа?
В графе с весовой функцией  строится каркас с помощью алгоритма Прима. Пусть
строится каркас с помощью алгоритма Прима. Пусть 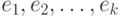 - список всех ребер каркаса в том порядке, в каком они добавлялись при построении. Какие из следующих утверждений верны для любого графа, любой весовой функции и любого
- список всех ребер каркаса в том порядке, в каком они добавлялись при построении. Какие из следующих утверждений верны для любого графа, любой весовой функции и любого 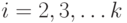 ?
?
Сколько различных наибольших паросочетаний имеется в графе 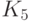 ?
?
Для некоторого графа с заданным в нем паросочетанием построено дерево достижимости T с корнем в свободной вершине a. Какие из следующих утверждений верны для любого графа, любого паросочетания и любого дерева достижимости?
Дан граф  с множеством ребер
с множеством ребер  . Для каких из перечисленных ниже семейств
. Для каких из перечисленных ниже семейств  подмножеств множества
подмножеств множества  пара
пара 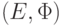 является матроидом для любого графа
является матроидом для любого графа  ?
?
Пусть 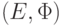 - матроид и на множестве
- матроид и на множестве  задана весовая функция
задана весовая функция  с вещественными значениями. Что произойдет, если к нему применить алгоритм СПО, в котором на первом этапе элементы множества
с вещественными значениями. Что произойдет, если к нему применить алгоритм СПО, в котором на первом этапе элементы множества  упорядочиваются не по убыванию, а по возрастанию весов?
упорядочиваются не по убыванию, а по возрастанию весов?
В графе K7 все ребра некоторого гамильтонова цикла имеют вес 2, а все остальные ребра - вес 5. Каков будет степень корня у дерева, построенного для этого графа с помощью алгоритма Дейкстры?
Каркасы, построенные для некоторого графа с помощью алгоритмов Прима, Крускала и Дейкстры, имеют соответственно веса a, b и c. Какое из следующих соотношений обязательно выполняются для этих чисел?
В полном графе с множеством вершин {1, 2, 3, 4, 5, 6} каждое ребро ориентировано от вершины с меньшим номером к вершине с большим и имеет пропускную способность 1. Какова наибольшая величина потока от вершины 1 к вершине 6?
Какие из следующих утверждений верны?
Что происходит с хроматическим числом графа при удалении ребра?
Алгоритм поиска в глубину применяется к планарному графу, заданному матрицей смежности. Какие оценки трудоемкости справедливы в этом случае?
Какие из следующих условий являются необходимыми и достаточными для того, чтобы граф имел хроматический индекс 2?
Чему равно число независимости графа Q3?
Сколько ребер имеет граф пересечений граней трехмерного куба?
В каких из следующих случаев можно утверждать, что путь, соединяющий вершины x и y в BFS-дереве, является кратчайшим путем между ними в графе?
Какие из следующих утверждений верны?
Сколько имеется абстрактных деревьев с 6 вершинами?
Как может измениться цикломатическое число при добавлении к графу нового ребра?
Сколько имеется абстрактных графов с 5 вершинами, не являющихся хордальными?
Сколько ребер нужно удалить из наименьшего реберного покрытия графа 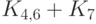 , чтобы получить наибольшее паросочетание этого графа?
, чтобы получить наибольшее паросочетание этого графа?
Что происходит с диаметром графа при удалении ребра?
Сколько имеется абстрактных двусвязных графов с 4 вершинами?
Для двудольного графа с заданным в нем паросочетанием построено дерево достижимости T с корнем в свободной вершине a. Какие из следующих утверждений верны?
В полном графе с множеством вершин {1, 2, 3, 4, 5, 6} каждое ребро ориентировано от вершины с меньшим номером к вершине с большим. Ребро 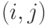 ,
, 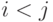 , имеет пропускную способность i . Какова наибольшая величина потока от вершины 1 к вершине 6?
, имеет пропускную способность i . Какова наибольшая величина потока от вершины 1 к вершине 6?
Сколько имеется абстрактных обыкновенных графов с набором степеней (2, 2, 4, 4, 5, 5)?
Для некоторого графа построено DFS-дерево T с корнем a. Ребро графа (x,y) дереву не принадлежит. Какие из следующих соотношений могут выполняться (d обозначает расстояние между вершинами в дереве T)?
Сколько имеется абстрактных обыкновенных графов с набором степеней (3, 3, 3, 3, 4, 4)?
В графе 6 вершин и 8 ребер. Сколько единиц будет в матрице инцидентности дополнительного графа?
Сколько имеется абстрактных графов с 4 вершинами диаметра 2?
Какие из следующих утверждений верны для любого графа и любого его подграфа
и любого его подграфа ?
?
Какие из следующих графов планарны?
Поиск в ширину применяется к графу  . Какой будет высота BFS-дерева?
. Какой будет высота BFS-дерева?
Какие из следующих равенств выполняются для любых графов G, H и F с одним и тем же множеством вершин
Какова будет наибольшая из длин фундаментальных циклов относительно каркаса, построенного с помощью поиска в глубину для графа K3,5?
Какие из следующих утверждений верны?
Какие из следующих равенств выполняются для любых графов G1 и G2?
Что произойдет, если описанный в лекции 8 алгоритм построения эйлерова цикла применить к графу Pn(без предварительной проверки четности степеней)?
Какие из следующих операций сохраняют свойство хордальности, т. е. при применении операции к хордальному графу всегда получается хордальный граф?
Пусть 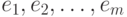 - список ребер графа в порядке убывания весов. Какие из следующих утверждений верны для любого графа и любой весовой функции?
- список ребер графа в порядке убывания весов. Какие из следующих утверждений верны для любого графа и любой весовой функции?
Для некоторого графа построено BFS-дерево с корнем  . Ребро графа
. Ребро графа 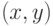 дереву не принадлежит. Какие из следующих соотношений могут выполняться (
дереву не принадлежит. Какие из следующих соотношений могут выполняться ( обозначает расстояние между вершинами в графе)?
обозначает расстояние между вершинами в графе)?
Пусть  и
и  - ребра с наименьшими весами в некотором взвешенном графе, причем
- ребра с наименьшими весами в некотором взвешенном графе, причем  . Какие из следующих утверждений верны для любого графа и любой весовой функции?
. Какие из следующих утверждений верны для любого графа и любой весовой функции?
Сколько листьев будет в дереве вариантов при применении описанного в лекции 10 переборного алгоритма раскраски вершин к графу C4 ?
В графе K6 все ребра некоторого гамильтонова цикла имеют вес 2, а все остальные ребра - вес 5. Каков будет вес дерева, построенного для этого графа с помощью алгоритма Дейкстры?
Какие из следующих равенств выполняются для любых графов G1 и G2?
Сколько различных абстрактных двудольных графов можно получить, добавляя одно ребро к графу  ?
?
Сколько имеется абстрактных обыкновенных графов с 4 вершинами и 3 ребрами?
Сколько имеется абстрактных ориентированных графов без петель и кратных ребер с 3 вершинами и 3 ребрами?
Алгоритм поиска в ширину применяется к планарному графу, заданному списками смежности. Какие оценки трудоемкости справедливы в этом случае?
Сколько максимальных независимых множеств имеется у графа P5?
Какие из следующих равенств выполняются для любых графов G1 и G2?
Дано непустое конечное множество  и семейство его подмножеств
и семейство его подмножеств  . В каких из перечисленных ниже случаев пара
. В каких из перечисленных ниже случаев пара 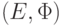 является матроидом?
является матроидом?
В каких из следующих графов имеется гамильтонов цикл?
Сколько различных каркасов имеется у графа  ?
?
Сколько имеется абстрактных графов с 4 вершинами, у которых центр состоит ровно из 2 вершин?
Поиск в глубину применяется к графу  . Какова будет высота DFS-дерева?
. Какова будет высота DFS-дерева?
В графе с 10 вершинами вес каждого ребра равен 1 или 2, причем ребра веса 2 порождают остовный подграф с тремя компонентами связности. Чему равен вес оптимального каркаса для этого графа?
Сколько имеется связных абстрактных графов с 5 вершинами, в которых существует эйлеров цикл?
Корневое дерево имеет радиус 4, а у каждой его вершины не более двух сыновей. Каково наибольшее число вершин в таком дереве?
Какие из следующих утверждений верны?
Сколько существует абстрактных связных графов с 5 вершинами, имеющих ровно два блока?
Алгоритм поиска в глубину применяется к лесу, заданному списками смежности. Какие оценки трудоемкости справедливы в этом случае?
Сколько имеется неориентированных графов, в которых допускаются петли, но не кратные ребра, с множеством вершин {1, 2, 3}?
Пусть h - высота BFS-дерева, построенного для графа G. Какие из следующих утверждений верны?
Что происходит с диаметром графа при удалении вершины?

 строится каркас с помощью алгоритма Крускала. Пусть
строится каркас с помощью алгоритма Крускала. Пусть 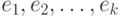 - список всех ребер каркаса в том порядке, в каком они добавлялись при построении. Какие из следующих утверждений верны для любого графа, любой весовой функции и любого
- список всех ребер каркаса в том порядке, в каком они добавлялись при построении. Какие из следующих утверждений верны для любого графа, любой весовой функции и любого 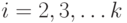 ?
?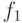 и
и 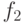 является потоком в некоторой сети. Какие из следующих функций обязательно будут потоками в той же сети?
является потоком в некоторой сети. Какие из следующих функций обязательно будут потоками в той же сети?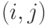 ,
, 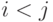 , имеет пропускную способность i . Какова наибольшая величина потока от вершины 1 к вершине 6?
, имеет пропускную способность i . Какова наибольшая величина потока от вершины 1 к вершине 6? . Ребро графа
. Ребро графа 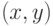 дереву не принадлежит. Какие из следующих соотношений могут выполняться (
дереву не принадлежит. Какие из следующих соотношений могут выполняться ( обозначает расстояние между вершинами в графе)?
обозначает расстояние между вершинами в графе)?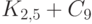 , чтобы получить наименьшее реберное покрытие этого графа?
, чтобы получить наименьшее реберное покрытие этого графа? с множеством вершин
с множеством вершин 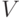 ,
,  - семейство всех независимых множеств вершин этого графа (пустое множество тоже считается независимым). В каких из перечисленных ниже случаев пара
- семейство всех независимых множеств вершин этого графа (пустое множество тоже считается независимым). В каких из перечисленных ниже случаев пара 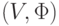 является матроидом,?
является матроидом,? имеет 4 вершины, а в его матрице смежности 8 единиц. Граф
имеет 4 вершины, а в его матрице смежности 8 единиц. Граф  имеет 5 вершин, а в его матрице смежности 12 единиц. Сколько единиц будет в матрице смежности графа
имеет 5 вершин, а в его матрице смежности 12 единиц. Сколько единиц будет в матрице смежности графа  ?
? 12 ребер. Сколько ребер в графе
12 ребер. Сколько ребер в графе  ?
? строится каркас с помощью алгоритма Прима. Пусть
строится каркас с помощью алгоритма Прима. Пусть 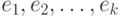 - список всех ребер каркаса в том порядке, в каком они добавлялись при построении. Какие из следующих утверждений верны для любого графа, любой весовой функции и любого
- список всех ребер каркаса в том порядке, в каком они добавлялись при построении. Какие из следующих утверждений верны для любого графа, любой весовой функции и любого 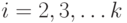 ?
? с множеством ребер
с множеством ребер  . Для каких из перечисленных ниже семейств
. Для каких из перечисленных ниже семейств  подмножеств множества
подмножеств множества  пара
пара 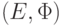 является матроидом для любого графа
является матроидом для любого графа  ?
?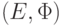 - матроид и на множестве
- матроид и на множестве  задана весовая функция
задана весовая функция  с вещественными значениями. Что произойдет, если к нему применить алгоритм СПО, в котором на первом этапе элементы множества
с вещественными значениями. Что произойдет, если к нему применить алгоритм СПО, в котором на первом этапе элементы множества  упорядочиваются не по убыванию, а по возрастанию весов?
упорядочиваются не по убыванию, а по возрастанию весов?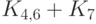 , чтобы получить наибольшее паросочетание этого графа?
, чтобы получить наибольшее паросочетание этого графа?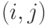 ,
, 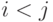 , имеет пропускную способность i . Какова наибольшая величина потока от вершины 1 к вершине 6?
, имеет пропускную способность i . Какова наибольшая величина потока от вершины 1 к вершине 6?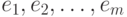 - список ребер графа в порядке убывания весов. Какие из следующих утверждений верны для любого графа и любой весовой функции?
- список ребер графа в порядке убывания весов. Какие из следующих утверждений верны для любого графа и любой весовой функции? . Ребро графа
. Ребро графа 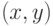 дереву не принадлежит. Какие из следующих соотношений могут выполняться (
дереву не принадлежит. Какие из следующих соотношений могут выполняться ( обозначает расстояние между вершинами в графе)?
обозначает расстояние между вершинами в графе)? и
и  - ребра с наименьшими весами в некотором взвешенном графе, причем
- ребра с наименьшими весами в некотором взвешенном графе, причем  . Какие из следующих утверждений верны для любого графа и любой весовой функции?
. Какие из следующих утверждений верны для любого графа и любой весовой функции? и семейство его подмножеств
и семейство его подмножеств  . В каких из перечисленных ниже случаев пара
. В каких из перечисленных ниже случаев пара 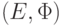 является матроидом?
является матроидом?