Требуется оценить вероятность 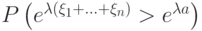 . Что получиться в результате применения неравенства Маркова?
. Что получиться в результате применения неравенства Маркова?
(Отметьте один правильный вариант ответа.)
Варианты ответа
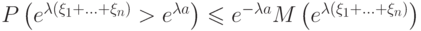 (Верный ответ)
(Верный ответ)
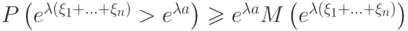
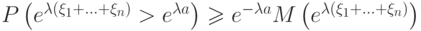


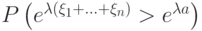 . Что получиться в результате применения неравенства Маркова?
. Что получиться в результате применения неравенства Маркова?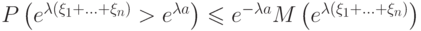 (Верный ответ)
(Верный ответ)
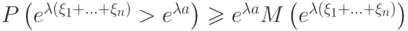
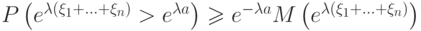

 . Какое условие на
. Какое условие на 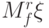 -
-  -ые факториальные моменты должно выполняться, чтобы
-ые факториальные моменты должно выполняться, чтобы 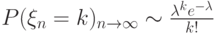 ?
?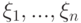 - последовательность независимых в совокупности случайных величин, для которых дисперсия конечна
- последовательность независимых в совокупности случайных величин, для которых дисперсия конечна 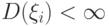 и сходится ряд
и сходится ряд 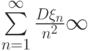 . С каким типом сходимости
. С каким типом сходимости 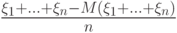 сходится к
сходится к  при
при 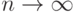 ?
?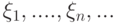 . Обозначим
. Обозначим 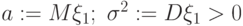 . Тогда с каким типом сходимости при
. Тогда с каким типом сходимости при 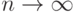 случайная величина
случайная величина  сходится к
сходится к 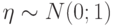 ?
?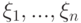 - последовательность независимых в совокупности и одинакового распределенных случайных величин, для которых математическое ожидание конечно
- последовательность независимых в совокупности и одинакового распределенных случайных величин, для которых математическое ожидание конечно 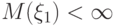 . С каким типом сходимости
. С каким типом сходимости 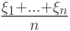 сходится к
сходится к  при
при 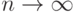 ?
? вероятность ровно
вероятность ровно  успехов в
успехов в  испытаниях по схеме Бернулли, если вероятность успеха в одном испытании
испытаниях по схеме Бернулли, если вероятность успеха в одном испытании  зависит от количества испытаний
зависит от количества испытаний  , зависимость
, зависимость 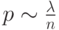 , где постоянная
, где постоянная  ?
?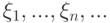 . Обозначим
. Обозначим 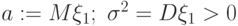 . Чему равна характеристическая функция для
. Чему равна характеристическая функция для  ?
?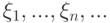 , у которых математическое ожидание конечно
, у которых математическое ожидание конечно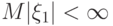 . C каким самым сильным типом сходимости при
. C каким самым сильным типом сходимости при 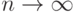 последоваетельность случайных величин
последоваетельность случайных величин 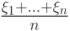 сходится к
сходится к  ?
?