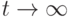Найдите решение уравнения 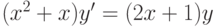 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 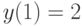 . В ответе укажите его значение при
. В ответе укажите его значение при 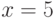
(Отметьте один правильный вариант ответа.)
Варианты ответа
30(Верный ответ)
20
10
40

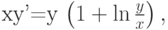
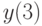 .
.  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  . В ответе укажите его значение при
. В ответе укажите его значение при 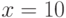
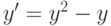 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 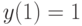 . В ответе укажите его значение при
. В ответе укажите его значение при 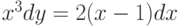 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  . В ответе укажите его значение при
. В ответе укажите его значение при 
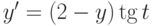 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  . В ответе укажите его значение при
. В ответе укажите его значение при 
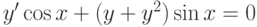 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 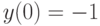 . В ответе укажите его значение при
. В ответе укажите его значение при 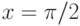
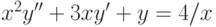 при
при  . Найдите решение, удовлетворяющее начальным условиям
. Найдите решение, удовлетворяющее начальным условиям 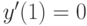 . В ответе укажите его значение
. В ответе укажите его значение 
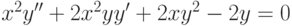 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: 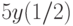

 . В ответе укажите его значение
. В ответе укажите его значение  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 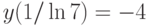 . В ответе укажите его предел при
. В ответе укажите его предел при