Дифференциальные уравнения - ответы
Количество вопросов - 299
Методом введения параметра найдите решение уравнения 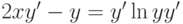 с начальными условиями
с начальными условиями  ,
, 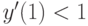 . При каком
. При каком  оно пересекает прямую
оно пересекает прямую 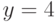 ?
?
Отыскав первый интеграл, найдите решение системы дифференциальных уравнений 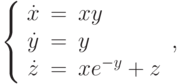 удовлетворяющее начальным условиям
удовлетворяющее начальным условиям 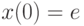 ,
,  и
и  . В ответе укажите значение
. В ответе укажите значение 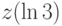 .
.
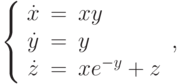
Найдите решение уравнения 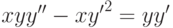 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: 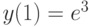 ,
,  . В ответе укажите его значение
. В ответе укажите его значение  при
при 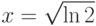
С помощью матричной экспоненты решите линейную однородную систему 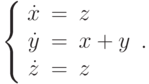 В ответе укажите значение
В ответе укажите значение  при
при 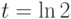 для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям  .
.
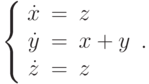
Отыскав первый интеграл, найдите решение системы дифференциальных уравнений  удовлетворяющее начальным условиям
удовлетворяющее начальным условиям 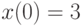 ,
,  и
и  . В ответе укажите значение
. В ответе укажите значение  .
.

Найдите функцию  , удовлетворяющую дифференциальному уравнению
, удовлетворяющую дифференциальному уравнению  и начальному условию
и начальному условию  В ответе укажите значение
В ответе укажите значение 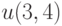 .
.


Решите неоднородную систему 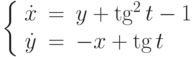 методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям  . В ответе укажите значение
. В ответе укажите значение 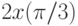 .
.
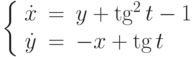
В баке находится 100 л раствора, содержащего 1 кг соли. В бак непрерывно подаётся вода (5 л в минуту), которая перемешивается с имеющимся раствором. Смесь вытекает с той же скоростью. Сколько граммов соли останется в баке через час? (Ответ округлить до целого числа.)
Найдите траекторию, проходящую через точку  и ортогональную семейству кривых
и ортогональную семейству кривых 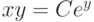 . Укажите значения
. Укажите значения  , при котором она пересекает прямую
, при котором она пересекает прямую 
Чайник за 10 минут остыл от 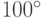 до
до  . Температура воздуха в комнате
. Температура воздуха в комнате  . За сколько минут чайник остынет от
. За сколько минут чайник остынет от  до
до  ? (Скорость остывания тела пропорциональна разности температур тела и окружающей среды.)
? (Скорость остывания тела пропорциональна разности температур тела и окружающей среды.)
Парашютист прыгнул с высоты 1,5 км и раскрыл парашют на высоте 0,5 км. Сколько секунд он падал до раскрытия парашюта? (Ответ округлить до целого числа.) Известно, что предельная скорость падения человека в воздухе нормальной плотности равна 50 м/с. Изменением плотности с высотой пренебречь. Сопротивление воздуха пропорционально квадрату скорости.
Найдите решение уравнения 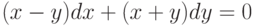 , проходящее через точку
, проходящее через точку  . В какой точке оно пересекает окружность с центром в начале координат и радиусом
. В какой точке оно пересекает окружность с центром в начале координат и радиусом 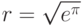 ?
?
Решите уравнение Эйлера 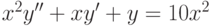 при
при  . Найдите решение, удовлетворяющее начальным условиям
. Найдите решение, удовлетворяющее начальным условиям 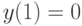 ,
, 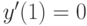 . В ответе укажите его значение
. В ответе укажите его значение 
Составьте линейное однородное дифференциальное уравнение с постоянными вещественными коэффициентами 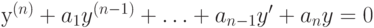 наименьшего порядка
наименьшего порядка  , которое имеет частные решения
, которое имеет частные решения  и
и 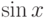 . В ответе укажите сумму
. В ответе укажите сумму 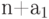
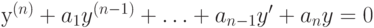
С помощью матричной экспоненты решите линейную однородную систему 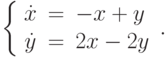 В ответе укажите значение
В ответе укажите значение  при
при  для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям 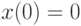 ,
,  .
.
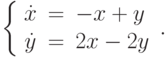
С помощью матричной экспоненты решите линейную однородную систему  В ответе укажите значение
В ответе укажите значение  при
при 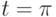 для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям  ,
, 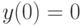 .
.

С помощью матричной экспоненты решите линейную однородную систему 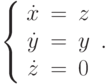 В ответе укажите значение
В ответе укажите значение  при
при  для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям  ,
,  ,
,  .
.
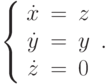
При каком наименьшем  уравнение вида
уравнение вида 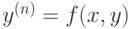 , где
, где  - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции  и
и  ?
?
При каком наименьшем  уравнение вида
уравнение вида 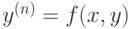 , где
, где  - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции 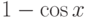 и
и 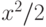 ?
?
Методом введения параметра найдите решение уравнения 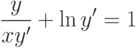 с начальными условиями
с начальными условиями  ,
,  . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
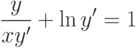
Найдите все значения вещественного параметра  , при которых особая точка системы
, при которых особая точка системы  асимптотически устойчива.
асимптотически устойчива.

Отыскав первый интеграл, найдите решение системы дифференциальных уравнений 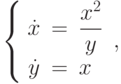 удовлетворяющее начальным условиям
удовлетворяющее начальным условиям 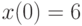 и
и  . В ответе укажите значение
. В ответе укажите значение  .
.
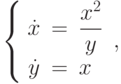
Найдите общее решение системы дифференциальных уравнений 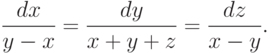 В ответе укажите абсциссу точки пересечения плоскости
В ответе укажите абсциссу точки пересечения плоскости 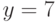 и решения, проходящего через точку
и решения, проходящего через точку 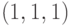 .
.
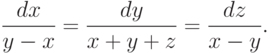
Найдите функцию  , удовлетворяющую дифференциальному уравнению
, удовлетворяющую дифференциальному уравнению 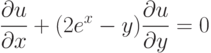 и начальному условию
и начальному условию  В ответе укажите значение
В ответе укажите значение 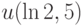 .
.
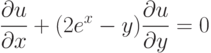

Найдите функцию  , удовлетворяющую дифференциальному уравнению.
, удовлетворяющую дифференциальному уравнению.  и начальному условию
и начальному условию  В ответе укажите значение
В ответе укажите значение 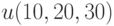 .
.


Найдите функцию  , удовлетворяющую дифференциальному уравнению
, удовлетворяющую дифференциальному уравнению 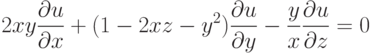 и начальному условию
и начальному условию 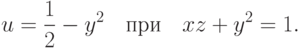 В ответе укажите значение
В ответе укажите значение  при
при 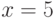 ,
,  и
и 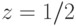 .
.
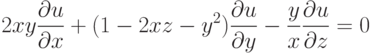
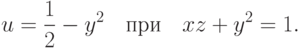
Найти матрицу  линейной однородной системы
линейной однородной системы 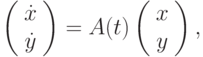 зная её фундаментальную матрицу
зная её фундаментальную матрицу  В ответе укажите значение суммы всех элементов найденной матрицы при
В ответе укажите значение суммы всех элементов найденной матрицы при 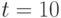
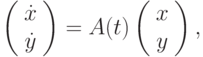

Вычислите значение при 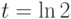 определителя Вронского двух вектор-функций
определителя Вронского двух вектор-функций 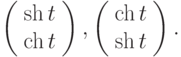 Являются ли эти вектор-функции линейно зависимыми?
Являются ли эти вектор-функции линейно зависимыми?
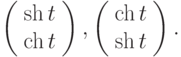
Вычислите значение при 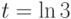 определителя Вронского трёх вектор-функций
определителя Вронского трёх вектор-функций 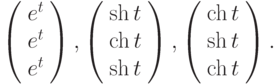 Являются ли эти вектор-функции линейно зависимыми?
Являются ли эти вектор-функции линейно зависимыми?
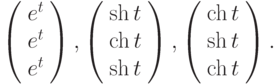
Два решения  и
и  системы
системы 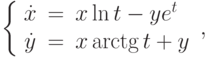 удовлетворяют начальным условиям:
удовлетворяют начальным условиям:  Найдите значение их определителя Вронского при
Найдите значение их определителя Вронского при 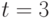 .
.
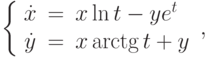
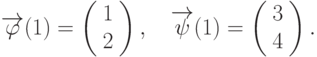
Система  имеет решение
имеет решение 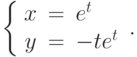 Найдите решение, удовлетворяющее начальным условиям
Найдите решение, удовлетворяющее начальным условиям  . В ответе укажите значение
. В ответе укажите значение  .
.

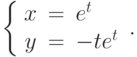
Решите неоднородную систему  методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям 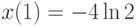 ,
,  . В ответе укажите значение
. В ответе укажите значение 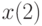 .
.

Вычислите определитель Вронского системы, состоящей из функций  и
и  . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
Вычислите определитель Вронского системы, состоящей из функций  ,
,  и
и  . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
Составьте линейное однородное дифференциальное уравнение вида 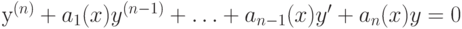 наименьшего порядка
наименьшего порядка  , которое имеет следующие частные решения:
, которое имеет следующие частные решения: 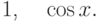 В ответе укажите
В ответе укажите 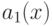 .
.
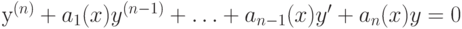
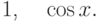
Известны два частных решения линейного неоднородного уравнения первого порядка: 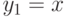 и
и 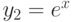 . Найдите решение с начальным условием
. Найдите решение с начальным условием  .
.
Решите неоднородное уравнение 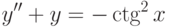 методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям  ,
, 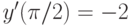 . В ответе укажите значение
. В ответе укажите значение  .
.
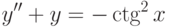
Решите неоднородное уравнение 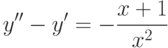 методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям 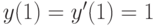 . В ответе укажите значение
. В ответе укажите значение  .
.
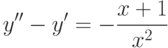
Напишите уравнение вида 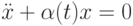 , которому удовлетворяет функция
, которому удовлетворяет функция 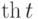 и найдите его решение с начальными условиями
и найдите его решение с начальными условиями  ,
,  . В ответе укажите значение
. В ответе укажите значение  .
.
В воздухе комнаты объёмом 200 куб. м содержится 0,15% углекислого газа. Вентилятор подаёт в минуту 20 куб. м воздуха содержащего 0,04% углекислого газа. Через сколько минут количество углекислого газа в воздухе комнаты уменьшится втрое? (Ответ округлить до целого числа.)
Решите неоднородную систему  методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям  . В ответе укажите значение
. В ответе укажите значение  .
.

За 30 дней распадается 50% радиоактивного вещества. За сколько дней распадётся 99% его первоначального количества? (Скорость распада радиоактивного вещества пропорциональна его оставшемуся количеству.)
При каком наименьшем  уравнение вида
уравнение вида 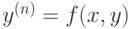 , где
, где  - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции  и
и 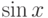 ?
?
Решите неоднородную систему  методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям 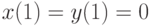 . В ответе укажите значение
. В ответе укажите значение 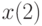 .
.

При каком наименьшем  уравнение вида
уравнение вида 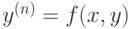 , где
, где  - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции  и
и 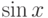 ?
?
Решите неоднородное уравнение  методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям  ,
, 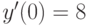 . В ответе укажите значение
. В ответе укажите значение  .
.

Найти матрицу  линейной однородной системы
линейной однородной системы 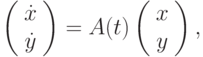 зная её фундаментальную матрицу
зная её фундаментальную матрицу  В ответе укажите значение суммы всех элементов найденной матрицы при
В ответе укажите значение суммы всех элементов найденной матрицы при 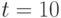 .
.
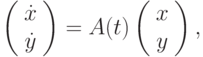

Найдите функцию  , удовлетворяющую дифференциальному уравнению
, удовлетворяющую дифференциальному уравнению 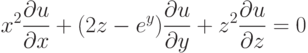 и начальному условию
и начальному условию 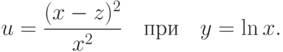 В ответе укажите значение
В ответе укажите значение  при
при  ,
, 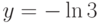 и
и 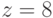 .
.
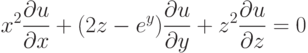
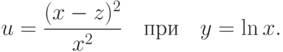
Методом введения параметра найдите решение уравнения  , проходящее через точку
, проходящее через точку 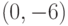 . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
Найдите все значения вещественного параметра $a$, при которых на допустимой экстремали достигается минимум ![\int\limits_0^1\left[y-2y'+a(y')^2\right]dx, \quad y(0)=0, \quad y(1)=1.](https://intuit.ru//sites/default/files/tex_cache/36d2df1d900430096e449499ecd422f9.png)
![\int\limits_0^1\left[y-2y'+a(y')^2\right]dx, \quad y(0)=0, \quad y(1)=1.](https://intuit.ru//sites/default/files/tex_cache/36d2df1d900430096e449499ecd422f9.png)
Найдите функцию $u$, удовлетворяющую дифференциальному уравнению 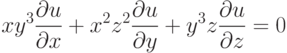 и начальному условию
и начальному условию  В ответе укажите значение
В ответе укажите значение 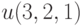 .
.
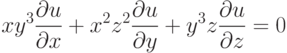

Найдите траекторию, проходящую через точку  и ортогональную семейству кривых
и ортогональную семейству кривых  . Укажите значение
. Укажите значение  , при котором она пересекает прямую
, при котором она пересекает прямую 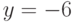
Составьте линейное однородное дифференциальное уравнение с постоянными вещественными коэффициентами 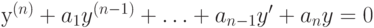 наименьшего порядка
наименьшего порядка  , которое имеет частное решение
, которое имеет частное решение  . В ответе укажите сумму
. В ответе укажите сумму 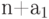
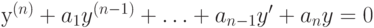
С помощью матричной экспоненты решите линейную однородную систему 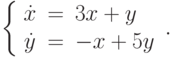 В ответе укажите значение
В ответе укажите значение  при
при 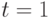 для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям  ,
, 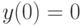 .
.
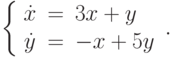
С помощью матричной экспоненты решите линейную однородную систему  В ответе укажите значение
В ответе укажите значение  при
при  для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям  .
.

Методом введения параметра найдите решение уравнения 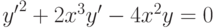 с начальными условиями
с начальными условиями 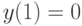 ,
, 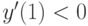 . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
Найдите все значения вещественного параметра  , при которых особая точка системы
, при которых особая точка системы 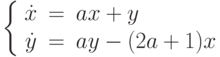 асимптотически устойчива.
асимптотически устойчива.
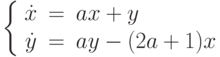
Найдите все значения вещественного параметра  , при которых особая точка системы
, при которых особая точка системы 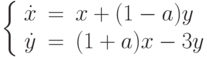 асимптотически устойчива.
асимптотически устойчива.
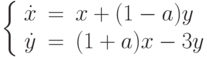
Отыскав первый интеграл, найдите решение системы дифференциальных уравнений  удовлетворяющее начальным условиям
удовлетворяющее начальным условиям 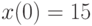 и
и  . В ответе укажите значение
. В ответе укажите значение 


Отыскав первый интеграл, найдите решение системы дифференциальных уравнений  удовлетворяющее начальным условиям
удовлетворяющее начальным условиям 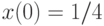 ,
, 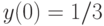 и
и 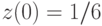 . В ответе укажите значение
. В ответе укажите значение 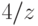 при
при 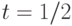 .
.

Найдите общее решение системы дифференциальных уравнений  В ответе укажите значение координаты
В ответе укажите значение координаты  точки пересечения плоскости
точки пересечения плоскости  и решения, проходящего через точку
и решения, проходящего через точку 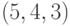 .
.

Найдите общее решение системы дифференциальных уравнений 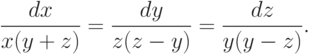 В ответе укажите абсциссу точки пересечения плоскости
В ответе укажите абсциссу точки пересечения плоскости  и решения, проходящего через точку
и решения, проходящего через точку 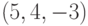 .
.
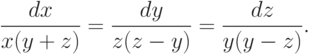
Найдите функцию  , удовлетворяющую дифференциальному уравнению
, удовлетворяющую дифференциальному уравнению  и начальному условию
и начальному условию  В ответе укажите значение
В ответе укажите значение 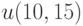 .
.


Найдите фундаментальную матрицу  системы
системы  если
если 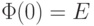 (
( - единичная матрица). В ответе укажите сумму собственных чисел матрицы
- единичная матрица). В ответе укажите сумму собственных чисел матрицы  .
.

Вычислите значение при $t=10$ определителя Вронского двух вектор-функций 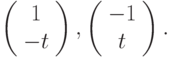 Являются ли эти вектор-функции линейно зависимыми?
Являются ли эти вектор-функции линейно зависимыми?
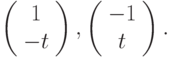
Вычислите значение при 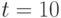 определителя Вронского двух вектор-функций
определителя Вронского двух вектор-функций 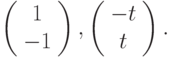 Являются ли эти вектор-функции линейно зависимыми?
Являются ли эти вектор-функции линейно зависимыми?
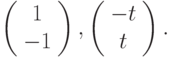
Два решения  и
и  системы
системы  удовлетворяют начальным условиям:
удовлетворяют начальным условиям: 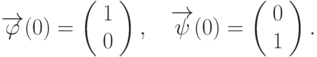 Найдите их определитель Вронского
Найдите их определитель Вронского 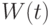 . В ответе укажите значение
. В ответе укажите значение 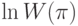 .
.

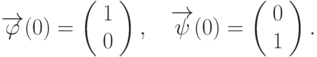
Система 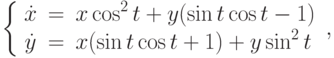 имеет решение
имеет решение 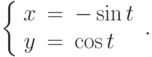 Найдите решение, удовлетворяющее начальным условиям
Найдите решение, удовлетворяющее начальным условиям  . В ответе укажите значение
. В ответе укажите значение  при
при  .
.
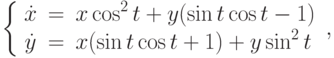
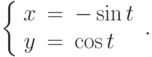
Вычислите определитель Вронского системы, состоящей из функций  и
и 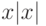 . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
Известны три частных решения линейного неоднородного уравнения второго порядка:  ,
, 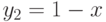 и
и  . Найдите решение с начальным условием
. Найдите решение с начальным условием  ,
, 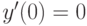 .
.
Решите неоднородное уравнение 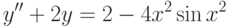 методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям 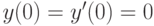 . В ответе укажите значение
. В ответе укажите значение  .
.
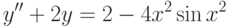
Вещественная функция  определена, непрерывна и положительна на всей числовой прямой. Какое наибольшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения
определена, непрерывна и положительна на всей числовой прямой. Какое наибольшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения 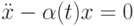 ?
?
Найдите все значения вещественного параметра  , при которых на допустимой экстремали достигается минимум
, при которых на допустимой экстремали достигается минимум ![\int\limits_0^1\left[x+x^2+y^2+a(y')^2\right]dx, \quad y(0)=0, \quad y(1)=1.](https://intuit.ru//sites/default/files/tex_cache/443f5840131669c1b8401fca46547606.png)
![\int\limits_0^1\left[x+x^2+y^2+a(y')^2\right]dx, \quad y(0)=0, \quad y(1)=1.](https://intuit.ru//sites/default/files/tex_cache/443f5840131669c1b8401fca46547606.png)
С помощью матричной экспоненты решите линейную однородную систему  В ответе укажите значение
В ответе укажите значение  при
при 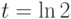 для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям  ,
, 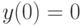 .
.

Решите уравнение Эйлера 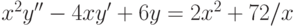 при
при  . Найдите решение, удовлетворяющее начальным условиям
. Найдите решение, удовлетворяющее начальным условиям 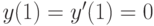 . В ответе укажите его значение
. В ответе укажите его значение 
Найдите наименьшее вещественное значение  , при котором краевая задача
, при котором краевая задача 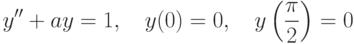 имеет бесконечно много решений.
имеет бесконечно много решений.
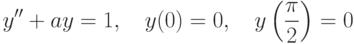
С помощью матричной экспоненты решите линейную однородную систему  В ответе укажите значение
В ответе укажите значение  при
при 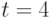 для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям 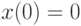 ,
,  .
.

Отыскав первый интеграл, найдите решение системы дифференциальных уравнений 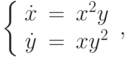 удовлетворяющее начальным условиям
удовлетворяющее начальным условиям  и
и  . В ответе укажите значение
. В ответе укажите значение 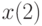 .
.
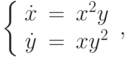
Найдите функцию  , удовлетворяющую дифференциальному уравнению
, удовлетворяющую дифференциальному уравнению 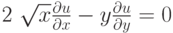 и начальному условию
и начальному условию  В ответе укажите значение
В ответе укажите значение  при
при 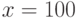 и
и 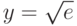 .
.
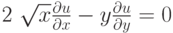

Найдите функцию  , удовлетворяющую дифференциальному уравнению
, удовлетворяющую дифференциальному уравнению  и начальному условию
и начальному условию  В ответе укажите значение
В ответе укажите значение  .
.


Вычислите значение при 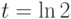 определителя Вронского двух вектор-функций
определителя Вронского двух вектор-функций 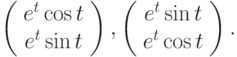 Являются ли эти вектор-функции линейно зависимыми?
Являются ли эти вектор-функции линейно зависимыми?
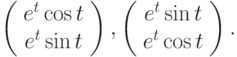
Система 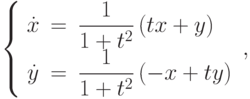 имеет решение
имеет решение 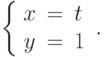 Найдите решение, удовлетворяющее начальным условиям
Найдите решение, удовлетворяющее начальным условиям  . В ответе укажите значение
. В ответе укажите значение 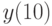 .
.
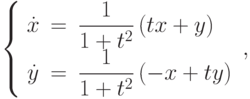
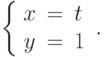
Решите неоднородную систему  методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям  . В ответе укажите значение
. В ответе укажите значение 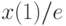 .
.

Вычислите определитель Вронского системы, состоящей из функций  ,
,  и
и  . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
Вычислите определитель Вронского системы, состоящей из функций  ,
, 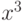 и
и 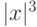 . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
Составьте линейное однородное дифференциальное уравнение вида 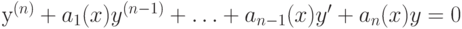 наименьшего порядка
наименьшего порядка  , которое имеет следующие частные решения:
, которое имеет следующие частные решения:  В ответе укажите
В ответе укажите 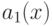 .
.
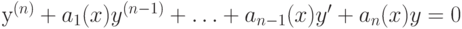

Известны три частных решения линейного неоднородного уравнения второго порядка:  ,
, 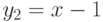 и
и 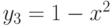 . Найдите решение с начальным условием
. Найдите решение с начальным условием 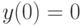 ,
, 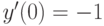 .
.
Решите неоднородное уравнение  методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям 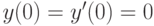 . В ответе укажите значение
. В ответе укажите значение 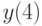 .
.

При каком наименьшем  уравнение вида
уравнение вида 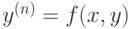 , где
, где  - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции  и
и 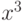 ?
?
Решите неоднородное уравнение 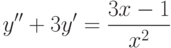 методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям 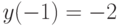 ,
, 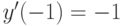 . В ответе укажите значение
. В ответе укажите значение 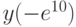 .
.
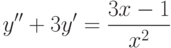
Составьте линейное однородное дифференциальное уравнение с постоянными вещественными коэффициентами 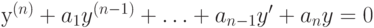 наименьшего порядка
наименьшего порядка  , которое имеет частное решение
, которое имеет частное решение 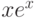 . В ответе укажите сумму
. В ответе укажите сумму 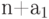
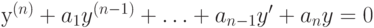
С помощью матричной экспоненты решите линейную однородную систему 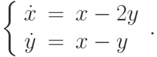 В ответе укажите значение
В ответе укажите значение  при
при  для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям 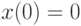 ,
,  .
.
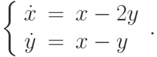
При каком наименьшем  уравнение вида
уравнение вида 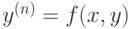 , где
, где  - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции  и
и 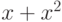 ?
?
Методом введения параметра найдите решение уравнения 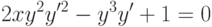 с начальными условиями
с начальными условиями 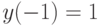 ,
, 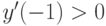 . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
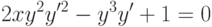
Найдите фундаментальную матрицу  системы
системы 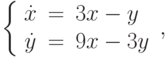 если
если 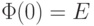 (
( - единичная матрица). В ответе укажите сумму всех элементов матрицы
- единичная матрица). В ответе укажите сумму всех элементов матрицы  .
.
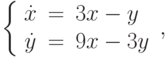
Вычислите определитель Вронского системы, состоящей из функций 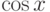 и
и 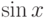 . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
Решите уравнение Эйлера 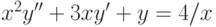 при
при  . Найдите решение, удовлетворяющее начальным условиям
. Найдите решение, удовлетворяющее начальным условиям 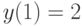 ,
, 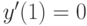 . В ответе укажите его значение
. В ответе укажите его значение 
Вычислите значение при 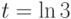 определителя Вронского трёх вектор-функций
определителя Вронского трёх вектор-функций  Являются ли эти вектор-функции линейно зависимыми?
Являются ли эти вектор-функции линейно зависимыми?

Составьте линейное однородное дифференциальное уравнение вида 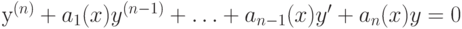 наименьшего порядка
наименьшего порядка  , которое имеет следующие частные решения:
, которое имеет следующие частные решения: 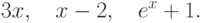 В ответе укажите
В ответе укажите 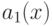 .
.
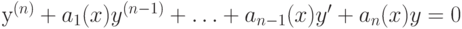
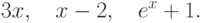
Вещественная функция  определена, непрерывна и положительна на всей числовой прямой. Какое наименьшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения
определена, непрерывна и положительна на всей числовой прямой. Какое наименьшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения 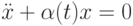 ?
?
Вещественная функция  определена, непрерывна и положительна на всей числовой прямой. Какое наименьшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения
определена, непрерывна и положительна на всей числовой прямой. Какое наименьшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения 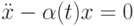 ?
?
Найдите траекторию, проходящую через точку  и ортогональную семейству кривых
и ортогональную семейству кривых  . Укажите значение
. Укажите значение  , при котором она пересекает прямую
, при котором она пересекает прямую 
Отыскав первый интеграл, найдите решение системы дифференциальных уравнений  удовлетворяющее начальным условиям
удовлетворяющее начальным условиям 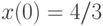 и
и 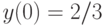 . В ответе укажите значение
. В ответе укажите значение 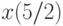 .
.

Решите неоднородную систему 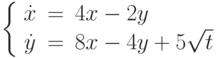 методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям  . В ответе укажите значение
. В ответе укажите значение 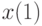 .
.
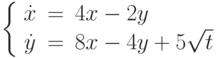

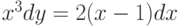 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  . В ответе укажите его значение при
. В ответе укажите его значение при 
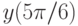 функции, удовлетворяющей дифференциальному уравнению
функции, удовлетворяющей дифференциальному уравнению  и начальному условию
и начальному условию 

 , проходящее через точку
, проходящее через точку 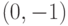 . При каком
. При каком  ?
?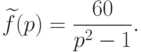
 .
.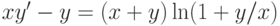
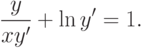
 ?
?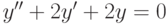 ,
, 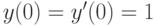 . В ответе укажите значение
. В ответе укажите значение 
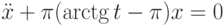 на интервале длины
на интервале длины  ?
?
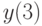
![\int\limits_1^3\left[8yy' \ln{x}-x(y')^2+6xy'\right]dx, \quad y(3)=15.](https://intuit.ru//sites/default/files/tex_cache/fd91aa0007ae190926cd6ba41e62b3f2.png)
 .
.![\int\limits_0^2\left[2xy'+(y')^2\right]dx, \quad y(0)=0.](https://intuit.ru//sites/default/files/tex_cache/afaf7fefe7bb878b10e01c296a48bb26.png)
 .
.
 , если
, если 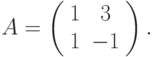

![\int\limits_0^{1}\left[2yy'+(y')^2\right]dx.](https://intuit.ru//sites/default/files/tex_cache/20ea9d6aff5f0759bcfb71157b16ff00.png)
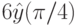 .
.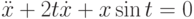 на отрезке длины 100?
на отрезке длины 100? ,
,  ,
, 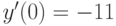 . В ответе укажите значение
. В ответе укажите значение 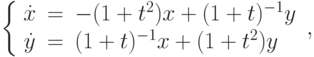
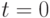 равно
равно 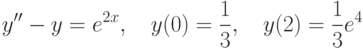
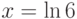
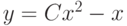
 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 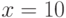
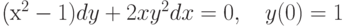
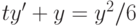 ,
,  . В ответе укажите значение её решения при
. В ответе укажите значение её решения при 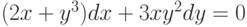 , проходящее через точку
, проходящее через точку  . При каком
. При каком  , проходящее через точку
, проходящее через точку 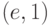 . При каком
. При каком  ?
?
 с начальным условием
с начальным условием  . В ответе укажите значение
. В ответе укажите значение 
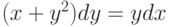

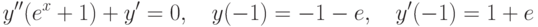

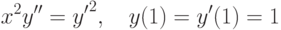

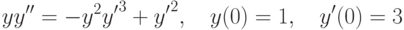
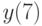
 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: 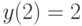 ,
,  . В ответе укажите значение
. В ответе укажите значение 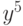 при
при 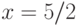
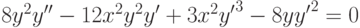 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: 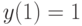 ,
, 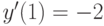 . В ответе укажите его значение
. В ответе укажите его значение  , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:  . В ответе укажите его значение
. В ответе укажите его значение 
 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: 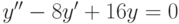 ,
, 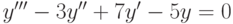 ,
, 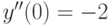 . В ответе укажите значение
. В ответе укажите значение 
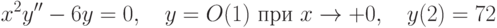


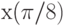 .
. 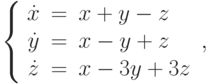
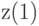 .
.
 . В ответе укажите значение
. В ответе укажите значение 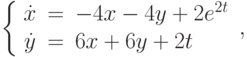

 от функции
от функции 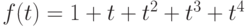 . В ответе укажите его значение
. В ответе укажите его значение 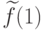 .
. преобразование Лапласа от оригинала
преобразование Лапласа от оригинала  .
.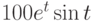 .
.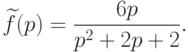
 .
.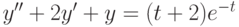 ,
, 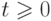 . В ответе укажите значение
. В ответе укажите значение  .
.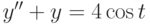 ,
, 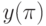 .
.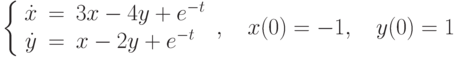
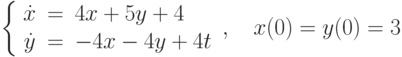
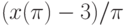 .
.![\int\limits_0^\pi\left[(y'+y)^2+2y\sin{x}\right]dx, \quad y(0)=0, \quad y(\pi)=1.](https://intuit.ru//sites/default/files/tex_cache/d52ede90e2b2ac064ee5865eb0216c40.png)
![\int\limits_2^4\left[x^2yy'+8x^2y-x^2(y')^2+(x-2)y^2\right]dx, \quad y(2)=0, \quad y(4)=-8.](https://intuit.ru//sites/default/files/tex_cache/2b251b8810c540b06a5193f6b30cf3de.png)
 .
.![\int\limits_1^2\left[x^2(y')^2+6y^2+x^3y\right]dx, \quad y(1)=11.](https://intuit.ru//sites/default/files/tex_cache/a995969362471b3255ba92dd650fa182.png)
![\int\limits_1^2\left[12y_1^2+y_2^2+x^2(y_1')^2+(y_2')^2\right]dx, \quad y_1(1)=1, \quad y_2(1)=e, \quad y_1(2)=8, \quad y_2(2)=e^2.](https://intuit.ru//sites/default/files/tex_cache/b2cb069dc5c5659bfa9fdce7d6f08c84.png)
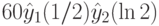 .
.![\int\limits_0^2\left[2xy+(y')^2\right]dx, \quad y(0)=0, \quad y(2)=6, \quad \int\limits_0^2 xy\,dx=8.](https://intuit.ru//sites/default/files/tex_cache/2a0239199bb35fcdc4a9fd747c5c8216.png)
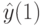 .
.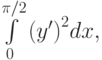

 при
при 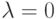 от решения
от решения 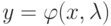 задачи Коши:
задачи Коши: 
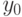 при
при  от решения
от решения 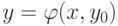 задачи Коши:
задачи Коши: 
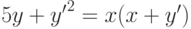 . При каком
. При каком 
 ?
?
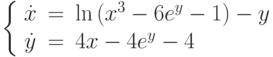

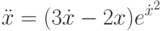
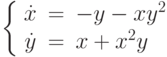
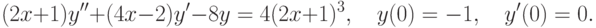
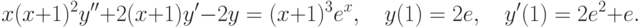
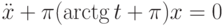 на отрезке длины
на отрезке длины 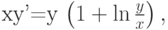
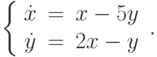
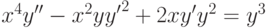 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:  . В ответе укажите его значение
. В ответе укажите его значение 

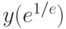
 определителя фундаментальной матрицы системы
определителя фундаментальной матрицы системы 
 равно
равно 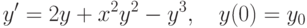
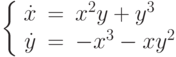
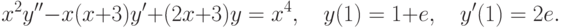

 ,
,  ,
, 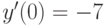 . В ответе укажите значение
. В ответе укажите значение 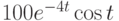 .
. , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: 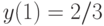 ,
, 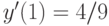 . В ответе укажите его значение
. В ответе укажите его значение 
![\int\limits_0^\pi\left[y^2+2y\cos{x}+(y')^2\right]dx, \quad y(0)=2, \quad y(\pi)=-2, \quad \int\limits_0^\pi y\cos{x}\,dx=\pi.](https://intuit.ru//sites/default/files/tex_cache/c72aff7d0e66270e5b85d45e8c9dcf6e.png)
 .
.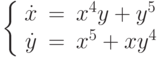
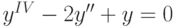 ,
,  ,
, 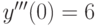 . В ответе укажите значение
. В ответе укажите значение 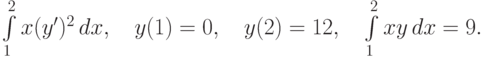
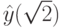 .
.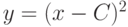
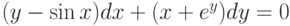
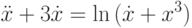
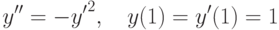
 .
.  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 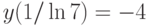 . В ответе укажите его предел при
. В ответе укажите его предел при 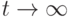
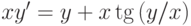
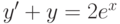 ,
,  . В ответе укажите значение её решения при
. В ответе укажите значение её решения при 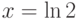
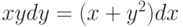
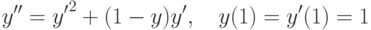

 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: 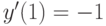 . В ответе укажите его значение
. В ответе укажите его значение 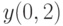
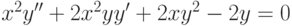 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: 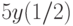
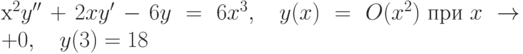

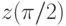 .
.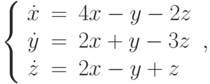
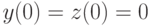 . В ответе укажите значение
. В ответе укажите значение 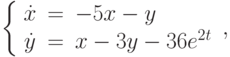
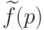 от постоянной функции
от постоянной функции 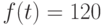 . В ответе укажите его значение при
. В ответе укажите его значение при 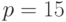 .
.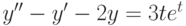 ,
, 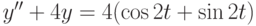 ,
, 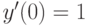 при
при 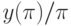 .
.
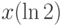 .
.
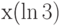 .
.![\int\limits_1^2\left[x(y')^2+\frac{y^2}{x}\right]dx, \quad y(1)=2, \quad y(2)=\frac52.](https://intuit.ru//sites/default/files/tex_cache/0b988a92b04a100e30d5837740f00e11.png)
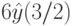 .
.![\int\limits_{-1}^1 e^x \left[(y')^2+6y^2\right]dx, \quad y(-1)=0, \quad y(1)=e^7-e^{-3}.](https://intuit.ru//sites/default/files/tex_cache/7f33acbfbfbd9b0c2f2970afbefb1589.png)
![\int\limits_1^{e}\left[x(y')^2+\frac{y^2}{x}+ \frac{2y\ln{x}}{x}\right]dx.](https://intuit.ru//sites/default/files/tex_cache/bfed68e4ed1a64c0e6972afb95a3de27.png)
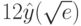 .
.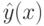 вариационной задачи:
вариационной задачи: ![\int\limits_0^{\pi/2}\left[y^2-2(y')^2+(y'')^2\right]dx, \quad y(0)=y'(0)=0, \quad y\left(\frac{\pi}{2}\right)=1, \quad y'\left(\frac{\pi}{2}\right)=\frac2\pi.](https://intuit.ru//sites/default/files/tex_cache/c6f90b5fb9d6faa69618569aaa3ff09b.png)
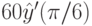 .
.
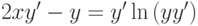 . При каком
. При каком  ?
?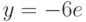 ?
?![\left\{\begin{array}{ccl} \dot{x} &=&\ln{(1-y)} \\ \dot{y} &=&\sqrt[3]{x-4y}+x-2\end{array}\right.](https://intuit.ru//sites/default/files/tex_cache/60a089c3f61f8766f9e3e2ff25b0da50.png)

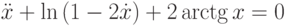

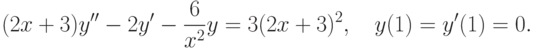
 на отрезке длины 100?
на отрезке длины 100?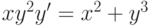
 .
.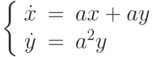
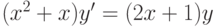 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![\ddot{x}+\sqrt[5]{5x+5\dot{x}}+\cos{\dot{x}}=0](https://intuit.ru//sites/default/files/tex_cache/f81b504920125bf26436b757f680eff2.png)
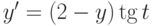 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 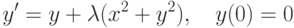
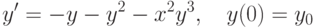
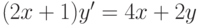 и начальному условию
и начальному условию 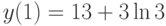
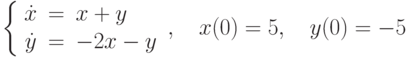
 .
.![\int\limits_0^{1}{\left[2yy'+\left(y'\right)^2\right]} dx, \quad\int\limits_0^{1}{\left[4xy'+yy'\right]} dx =8, \quad y(0)=y(1)=0.](https://intuit.ru//sites/default/files/tex_cache/2237d4daab8925d7f05e77ae586a90b4.png)
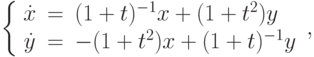
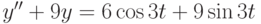 ,
,  .
.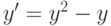 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 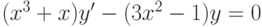 ,
,  . В ответе укажите значение её решения при
. В ответе укажите значение её решения при 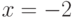
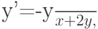
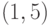 . При каком
. При каком 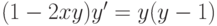
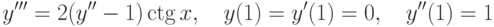
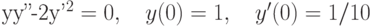

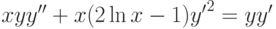 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: 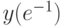
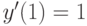 . В ответе укажите его значение
. В ответе укажите его значение 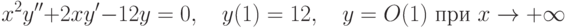

 , если
, если 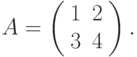
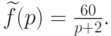
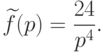
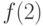 .
.![\int\limits_1^9\left[2y'-yy'+x(y')^2\right]dx, \quad y(1)=1, \quad y(9)=11.](https://intuit.ru//sites/default/files/tex_cache/dd1b394c9202aaf57c2ba0893fd7aa0d.png)
![\int\limits_1^2\left[x^2(y')^2+12y^2\right]dx, \quad y(1)=97.](https://intuit.ru//sites/default/files/tex_cache/05f3f0fada89f5a508641cf2e5b1139e.png)
![\int\limits_0^1\left[12(y'')^2-xy\right]dx, \quad y(0)=y'(0)=0, \quad y(2)=\frac{52}{5}, \quad y'(2)=24.](https://intuit.ru//sites/default/files/tex_cache/8f8955a69b4946da009ddf67eb717976.png)
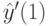 .
.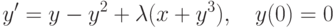
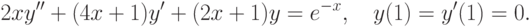
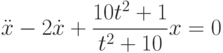
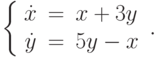
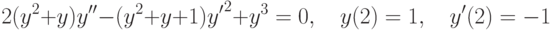
![\int\limits_1^4\left[\frac{2yy'}{x}-\frac{3y^2}{x^2}-(y')^2-\frac{y}{x}\right]dx, \quad y(1)=y(4)=4.](https://intuit.ru//sites/default/files/tex_cache/553cf0e4b0997da30003862afe871347.png)
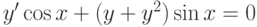 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 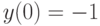 . В ответе укажите его значение при
. В ответе укажите его значение при 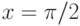
 , проходящего через точку
, проходящего через точку 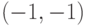
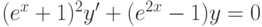 ,
, 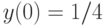 . В ответе укажите его предел при
. В ответе укажите его предел при 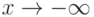
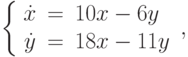
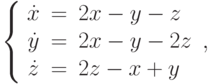
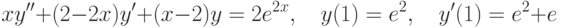
 на отрезке длины 100?
на отрезке длины 100?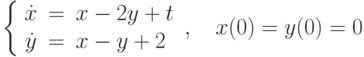
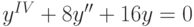 ,
, 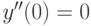 ,
, 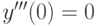 . В ответе укажите значение
. В ответе укажите значение 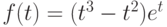 . В ответе укажите его значение при
. В ответе укажите его значение при 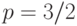 .
.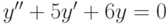 ,
, 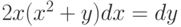
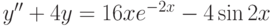 ,
, 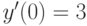 . В ответе укажите значение
. В ответе укажите значение 
 . В ответе укажите значение
. В ответе укажите значение 
![\int\limits_0^1\left[(y_1')^2+(y_2')^2\right]dx, \quad y_1(0)=y_2(0)=0, \quad y_1(1)=y_2(1)=1.](https://intuit.ru//sites/default/files/tex_cache/5934ab4116e98d4c5196f4c95bc1b711.png)
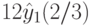 .
.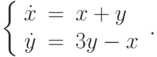

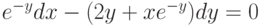 , проходящее через точку
, проходящее через точку 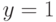 ?
? . В ответе укажите его значение при
. В ответе укажите его значение при 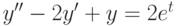 ,
,  .
.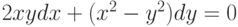 , проходящее через точку
, проходящее через точку  . При каком
. При каком 

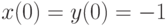 . В ответе укажите значение
. В ответе укажите значение  .
.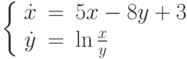
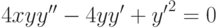 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: 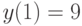 ,
, 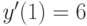 . В ответе укажите его значение
. В ответе укажите его значение 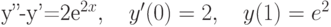
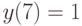 ,
,  . При каком
. При каком