Рассмотрим игру, в которой применяется минимаксная стратегия. Напомним, это означает, что в игре участвуют два противника, поочередно выполняющие ходы. Существует оценочная функция, которая выдает оценку (число) для каждой позиции после очередного хода. Положительное значение этой оценки рассматривается как выигрыш для одного игрока и как проигрыш для другого (игра с нулевой суммой). Рассмотрим дерево конкретной игры, в узлах которого записываются оценки позиций. Дерево зададим скобочной записью: (((5, 3) (6, -1, 8))((10, 6, 2) (-2, -4, -7)) )
Здесь цифры, заключенные в скобки - это оценки в листьях, принадлежащих одному родителю. Игрок на нижнем уровне выбирает минимальную оценку. Каково значение цены игры для этого дерева?
(Отметьте один правильный вариант ответа.)
Варианты ответа
3
5
10
-1
2(Верный ответ)
-7

 - полное бинарное дерево (каждый узел не являющийся листом дерева имеет двух потомков) число листьев в котором равно
- полное бинарное дерево (каждый узел не являющийся листом дерева имеет двух потомков) число листьев в котором равно 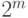 . Для обхода дерева применяется инфиксная процедура обхода (обойти левое дерево, обойти корень, обойти правое дерево). Каким по счету будет посещен корень дерева, если счет узлов начинается с 1)?
. Для обхода дерева применяется инфиксная процедура обхода (обойти левое дерево, обойти корень, обойти правое дерево). Каким по счету будет посещен корень дерева, если счет узлов начинается с 1)?

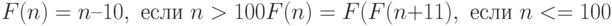
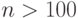 . А каковы ее значения при
. А каковы ее значения при 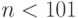 ? Оказывается, для таких
? Оказывается, для таких  функция имеет одно и то же значение. Какое?
функция имеет одно и то же значение. Какое?