При доказательстве утверждения "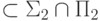 " используется:
" используется:
(Отметьте один правильный вариант ответа.)
Варианты ответа
замкнутость класса BPP относительно дополнений(Верный ответ)
нет верного ответа
открытость класса BPP относительно дополнений
тождественность класса BPP относительно дополнений

 , то разложение Шмидта имеет вид (
, то разложение Шмидта имеет вид (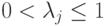 ,
, 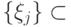 и
и 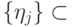 - ортонормированные вектора):
- ортонормированные вектора): - множество троек вида
- множество троек вида  , где
, где 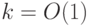 ,
, 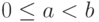 ,
, 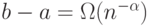 , (
, (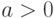 ), то для
), то для 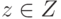 выполняются условия:
выполняются условия: ,
, 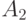 - неотрицательные операторы,
- неотрицательные операторы,  ,
, 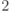 - их нулевые подпространства, причем
- их нулевые подпространства, причем 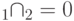 , ненулевые собственные числа
, ненулевые собственные числа 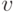 , где
, где 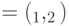 - угол между
- угол между  описанием схемы - приближенная реализация в стандартном базисе, а
описанием схемы - приближенная реализация в стандартном базисе, а  (
( - размер описания схемы). Тогда для
- размер описания схемы). Тогда для 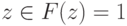 выполняется:
выполняется: , причем для любого чистого состояния
, причем для любого чистого состояния  выполняется свойство:
выполняется свойство: 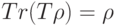 , то для любого оператора
, то для любого оператора  справедливым является равенство (
справедливым является равенство ( - некоторая фиксированная матрица плотности на пространстве
- некоторая фиксированная матрица плотности на пространстве  ):
): и
и  в формуле
в формуле  , которой должна удовлетворять квантовая схема
, которой должна удовлетворять квантовая схема  , вычисляющая
, вычисляющая  :
:![\Prob[G\setminus\big( \bigcup_i g_iX\big)\ne\emptyset]](https://intuit.ru//sites/default/files/tex_cache/bbebb8b3a266e675f2fb0d999601618d.png) не больше
не больше 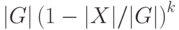 , где
, где  - некоторая группа, а
- некоторая группа, а  - случайное среди чисел от 1 до
- случайное среди чисел от 1 до 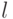 - нечетное, является:
- нечетное, является:![U_1[A_1],\dots, U_l[A_l]](https://intuit.ru//sites/default/files/tex_cache/83f6be2593a816115df273c5dce4beff.png) , где
, где 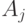 - множества битов,
- множества битов,  ,
,  - некоторое множество перестановок вида
- некоторое множество перестановок вида 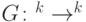 является:
является: